文/顏寧|綠色和平海洋專案主任
G20 高峰會剛落幕,各國領袖達成共識,致力在 2050 年前消除海洋垃圾,推動各國立法減塑。七月一日,臺灣將開始全亞洲第一個吸管限令:包括公部門、私立學校、百貨業與連鎖速食業內用皆不得提供吸管。預估一年可減少一億根吸管、約 1% 的吸管使用量。另環保署也將以此評估,決定是否明年擴大至外帶飲料與手搖杯業者。
塑膠垃圾對生物的影響:誤食、纏繞、改變生態系
網路上一則倒楣海龜鼻孔插進吸管,最後被救傷人員拔出的影片引發熱議。拔除過程中海龜痛苦不堪的畫面,不只讓人為之鼻酸,更掀起全球的拒用塑膠吸管熱潮。塑膠製品無法在自然環境中分解,一旦製造,至少會留存環境百年,造成許多生物因此纏繞或誤食,引發受傷、生病甚至死亡。
VIDEO 去年六月,鳥友在宜蘭大溪漁港拍到一隻鳳頭燕鷗,嘴喙上卡著一根塑膠吸管。今年同樣在燕鷗繁殖季節,又在蘭陽溪口發現一隻鳳頭燕鷗嘴喙卡著一個拉西環1 ,久久無法掙脫。從海洋保育署今年第一季的海龜及鯨豚通報救傷統計來看,漁業誤捕、漁業廢棄物與人造塑膠垃圾,已成為海洋生物擱淺死亡的主因之一 。2 而除了海鳥、海龜與鯨豚類容易獲得人們較多關注,其實越來越多魚類與無脊椎生物也因塑膠垃圾受害。
所有常用的塑膠都不是生物可分解的,它們會因陽光紫外線照射、風跟海浪等外力作用,裂解成不到 5 公釐的細小塑膠碎片。研究指出,每年最多有 1270 萬噸塑膠垃圾排入海中,相當於每分鐘一卡車的垃圾,源源不絕的往海裡倒 3 。其中 47% 是塑膠包裝和一次用的製品,材質以聚乙烯 (polyethylene,簡稱PE)和聚丙烯 (polypropylene,簡稱PP)為大宗。4 這些塑膠碎片分佈的範圍無遠弗屆,從極地到熱帶、從海水表面、沿岸到海洋最深處的馬里亞納海溝,都有微塑膠的蹤跡。
今年國家地理雜誌六月份的封面故事〈誰吃了海洋微塑膠 〉,報導美國海洋與大氣總署(NOAA)的科學家,在夏威夷外海油狀物區域做仔稚魚研究的駭人發現。簡單說,仔稚魚是新生的魚寶寶,經常聚集在油狀物匯集的海上覓食,而了解仔稚魚是研究漁業和魚群狀態非常重要的一環,不過因為仔稚魚又小又脆弱,使得仔稚魚的研究困難重重。研究人員驚訝的發現,在海面油狀物裡微塑膠濃度超高,微塑膠的量是仔稚魚的七倍以上,意謂著仔稚魚一張嘴就會吃到塑膠。
對新生仔稚魚來說,能吃到東西代表能多活一天,但若第一餐吃下的是塑膠,牠們可能等不到下一餐。雖然目前對魚類吃下塑膠所造成的傷害,科學界還沒有定論。但從實驗室裡的檢驗,讓科學家得以推測魚類的食慾、反應和成長速度都會受到影響;而仔稚魚生存狀態的細微變化,會轉為整體魚群的巨大變化,連帶影響到上層的食物鏈。
臺灣海生館副館長陳德豪帶領研究團隊,在恆春半島海域採集 117 隻珊瑚礁與洄游性魚種,發現九成五的魚類腸胃裡都有微塑膠,每隻魚體內至少有 5 個塑膠碎片,體型最大的鬼頭刀甚至有 32 個。另外,研究團隊也觀察海生館救傷收容的 21 隻海龜。從綠蠵龜、橄蠵龜和玳瑁的糞便裡,發現水果網袋、塑膠袋、糖果包裝紙、橡皮筋等,每隻海龜都吃下了數量不等的海洋廢棄物,比例高達百分之百,無一倖免。
受到塑膠污染影響的不只是野生動物,就連人類也開始受到大量消費塑膠製品的後果。世界自然基金會(WWF)的最新報告指出,平均每人每週吃下 5 公克的微塑膠,相當於每個禮拜吃掉一張信用卡。微塑膠無所不在,我們呼吸的空氣、我們吃的食物,以及我們喝的水都有微塑膠。那我們還能怎麼辦?面對不斷宣洩而下的水流,最重要的是關緊水龍頭的決心。
為什麼要從塑膠吸管禁起?
臺灣人一年用 30 億根吸管,算起來平均每人三天用一根,一天就有 800 萬根。雖然吸管在技術上是可以回收的,但可回收吸管的縣市只占少數5 ,要回收還需先沖洗乾淨,否則不但細菌孳生,更會影響回收品質。另外,吸管體積小質量輕,雖然技術上可回收,但回收利潤低,不足支付分類成本,經濟上沒有回收價值。
現行的機制底下,塑膠吸管回收並不符合經濟價值。 Image by Ulrike Leone from Pixabay
從在地環保團體過去十多年來的淨灘數據,吸管加上手搖杯、塑膠袋與免洗餐具等,總是蟬聯淨灘垃圾前五名。南非學者研究數個與開普敦城市不同距離的海灘發現,越輕、體積越小的垃圾,尤其是塑膠袋和食品包裝袋,因浮力小,主要聚集在鄰近城市區域的海岸上,不容易漂到太遠的地方。6 換句話說,這些日常飲食相關,多半是聚乙烯或聚丙烯材質的一次用塑膠製品,主要來自於本地的消費,而不是從國外海漂而來。它們隨著河流或排水溝散溢到環境,最後擱淺在海岸上。
用得多卻回收不易,最好的方式還是減少使用。 包括綠色和平在內等數個關心海廢議題的環保團體,與環保署共組海廢治理平台 ,在去年公佈的海廢治理行動方案中,特別將吸管、塑膠袋、免洗餐具與手搖杯納入減塑時程表中,從現在開始以限用、收費逐步走向 2030 年全面禁用。速食龍頭麥當勞率先停止提供塑膠吸管,改用就口杯鼓勵民眾直接喝。新的就口杯蓋,比起原本杯蓋加上吸管少了 0.4 克,麥當勞評估可減少 16% 塑膠。臺灣肯德基也跟進,鼓勵民眾撕開封膜飲用,預計一年減少 2 萬 5 千公斤塑膠量。
海灘上和日常飲食相關的一次用塑膠製品,由於質地較輕,主要是在地的產物,而不是從國外海漂而來。Image by Jasmin Sessler from Pixabay
生物可分解塑膠為什麼不好用?
減塑政策推得沸沸揚揚,在消費者改變習慣之前,替代材質 常是各方辯論的焦點。的確,市面上有具有潛力的替代材料,最普遍的生物可分解材質 PLA 與新興的 PHA 兩者都是可自然分解的塑膠,分解後最後剩下二氧化碳、水與其他殘留物。PLA 是利用玉米、木薯、麥桿和稻稈等植物中的澱粉和纖維素,經發酵後產生乳酸,將乳酸聚合,形成聚乳酸 (polylactic acid 或 polylactide,簡稱 PLA)。PHA則是厭氧菌合成的聚合物,好處是 PHA 可以在海洋中分解7 ,且 PHA 比 PLA 更耐熱,PLA 耐熱性只有 60 度,PHA 可耐熱到 140 度,比 PLA 更適合盛裝熱食。
實際上,這些「替代材質」最棘手的問題其實是:
(1)其實,可自然分解不是那麼「自然」,而是需要特定情境。PLA必需在工業堆肥的環境中才能分解,也就是高溫(60 度)、高濕與厭氧菌的環境下,可能在 60 天內可分解九成。但若環境條件不同,分解時間會更久(90 天到 180 天都有可能),分解程度也可能受到影響。而 PHA 在海中分解的速度也跟溫度、深度與菌種多寡有關。
(2)PLA 外觀與一般塑膠無異,消費者根本無法分辨。
(3)最後,PHA 雖比 PLA 耐熱、分解條件較寬鬆,但因為生產成本過高,目前還無法大量生產。
(4)目前 PLA 主要來源為玉米,可能面臨基因改造與競爭糧食種植的其他問題。
減塑政策與塑膠產業的拉鋸戰
臺灣的吸管禁令,先限制四大場所內用不提供塑膠吸管,雖然還沒有全面禁用,但已射出亞洲的第一箭。其他國家像蘇格蘭、萬那杜、牙買加、英格蘭(2020)和歐盟(2021)也陸續喊出禁用包括吸管在內的一次用塑膠製品。在國家層級之外,還有美國西雅圖、紐約、舊金山與加拿大溫哥華等城市,由當地市政府通過禁用吸管法案。
塑膠產品這麼多,該怎麼處理才能夠有效的減塑呢?Image by meineresterampe from Pixabay
不過,可別小看美國石化產業的遊說手腕,像佛羅里達就堅決不向減塑運動低頭,即使州內至少 10 個海灘小鎮都已開始實施吸管禁令,議會仍通過「在未來五年內都不准禁用塑膠吸管」的法案8 。 另外,星巴克雖然是最早喊出全球分店都停用塑膠吸管,但比起原來的杯蓋加吸管,新推出的寶寶杯蓋重量卻不減反增9 。作為全球飲品企業巨頭,建議星巴克可以多向臺灣麥當勞學習,也期待臺灣麥當勞能鼓勵其他地區分店跟進,全力減塑。
塑膠吸管限用,減塑的下一步呢?
縱觀各國,處理減塑最普遍的作法是對塑膠袋的管制,作法包括直接禁用、禁止一定厚度或付費取得。但塑膠產品這麼多,一項一項禁,真的來得及挽救我們的海洋?國際上腳步最快的是歐盟,與其分別設定個別塑膠製品的減量時程,直接魄力喊出 2021 年廣泛禁用 10 項海灘上常見的塑膠製品,以及寶特瓶的回收率需在 2025 年達到九成。而擁有全球最長海岸線的加拿大受到歐盟鼓舞,同樣訂定最快在 2021 年,禁用如塑膠袋、吸管、塑膠餐具杯碟與攪拌棒等有害的一次用塑膠製品。10 最近加州也跳脫過往與石化業者和塑膠製造業者,在保麗龍餐盒、塑膠袋和塑膠吸管戰場上的較勁,提出在 2030 年減少 75% 一次用塑膠包裝與製品的法案。11
「如果我們要修補這個系統,我們需要實際提出一個系統性的解決之道。」
——「東西的故事(Story of Stuff) 」倡議總監史提夫.威爾森(Stiv Wilson)
立法絕不是萬能,但是法令規範是最有效率的方式,配合後續的執法與民眾消費習慣改變,才是真正能降低塑膠使用量的關鍵。根據聯合國的統計,以目前實施減塑或限塑的國家來看,30%的國家在法律上路的第一年,塑膠袋的消費就顯著下降;但也有 20% 的國家沒什麼變化,原因是缺乏執法,以及缺乏民眾可負擔的替代產品。甚至,後者的國家還因此誕生塑膠袋走私與黑市的需求,或是以法律沒有規範的厚塑膠袋企圖規避。
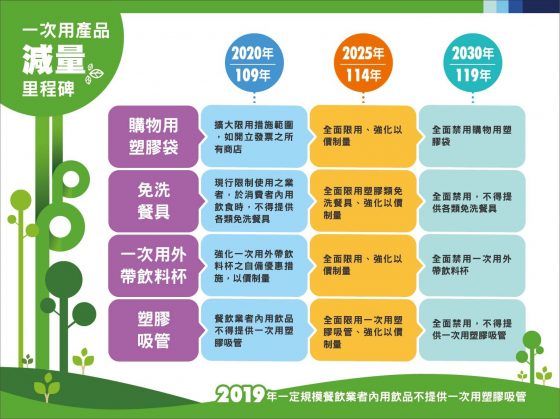
臺灣已公布四項一次用製品的減量時程表。圖/環保署一次用產品源頭減量宣導網
臺灣已跨出吸管限用的第一步,雖造成小小不便,仍有許多民意支持。相較於其他國家,目前臺灣已公布四項一次用製品的減量時程表,臺灣絕對有潛力作為亞洲的減塑領袖。未來我們也期待看到環保署能加快腳步,以歐盟為目標,並加強環境教育,鼓勵循環經濟的創新設計與服務,讓臺灣擺脫濫用塑膠的惡名。
參考資料與註解:
拉西環是洗滌塔的填充濾材,英文為 raschig ring(拉西環)或 packing(填充球、環保球、生化球)。濕式洗滌塔是一種將污染氣體大面積與液體接觸後,把有毒物質留在水中,乾淨空氣排放出去的裝置。焚化爐跟化工廠的煙囪都會安裝洗滌塔,以滿足排放標準。
三月擱淺的柯氏喙鯨胃裡有大量塑膠垃圾。海龜的部分,全台一共有 103 隻海龜通報案件,其中 82 隻已經死亡,19 隻是漁業誤捕,還有 3 隻遭廢棄漁網和漁線纏繞。
J. R. Jambeck, R. Geyer, C. Wilcox, T. R. Siegler, M. Perryman, A. Andrady, R. Narayan & K. L. Law (2015). Plastic waste inputs from land into the ocean. Science 347, 768–771.
Geyer, Roland, Jenna R. Jambeck, and Kara Lavender Law (2017). Production, use, and fate of all plastics ever made. Science Advances 3, e1700782.
根據中央社(2018)報導 ,目前可回收吸管縣市如下:新北市、基隆市、南投縣、嘉義市、台南市、金門縣。
Fazey, F.M.C. and Peter G. Ryan (2016) Debris size and buoyancy influence the dispersal distance of stranded litter. Marine Pollution Bulletin (110): 371-377.
Gross RA, Kalra B (2002) Biodegradable polymers for the environment. Science
Florida lawmakers pass bill prohibiting plastic straw bans in cities 依星巴克杯子大小不同,原本杯蓋加吸管重量為 3.23 與 3.55 克,新的寶寶杯蓋分別是 3.55 與 4.11 克
Canada to ban harmful single-use plastics and hold companies responsible for plastic waste California Circular Economy and Plastic Pollution Reduction Act. (2019-2020)