本文為系列文章,上一篇請見:搞懂「通用圖靈機」的第一站——康托爾的「無限樂園」 │《電腦簡史》數位時代(十二)
數學體系的的聖杯是否存在?——圖靈機的源頭
上一篇提到的無限這個原本大家都敬而遠之的怪物,還是被康托爾用集合論馴服了,集合論儼然成為建構數學體系的利器。然而過沒多久,英國哲學家與數學家羅素 (Bertrand Russell) 卻在 1901 年提出一個後來以他為名的「羅素悖論」(註一),指出集合論的矛盾之處,史稱「第三次數學危機」。
儘管幾位數學家著手修補,參考歐氏幾何有五大公設,也為集合論制定一些公設,將「樸素集合論」改造為沒有矛盾的「公設化集合論」,安然度過危機。但是數學體系接二連三出現裂縫,表示其中必有缺陷。大數學家希爾伯特 (David Hilbert) 因此呼籲重新審視所謂不證自明的公設或定理,從根基開始,重新打造完美無瑕的數學體系。

1928 年,希爾伯特在國際數學家大會上拋出三大提問:
一、數學是否完備?所謂完備是指每則陳述(例如畢氏定理)都可以被證明為真或為假。
二、數學是否一致?也就是同一則陳述不會有既被證明為真、又被證明為假的矛盾情況。
三、數學是否可以判定?意思是任何陳述都有一套明確的程序可以用來判定其真假。(例如希爾伯特列舉的 23 個懸而未決的數學問題,是否終究會找出證明的方法?)
基於數學以往幾次克服危機的歷史經驗,希爾伯特相信這三個提問的答案都是肯定的;1930 年他發表退休演說時,就以「我們必須知道,我們將會知道!」做為結語。這並不是希爾伯特一廂情願,事實上學界也都普遍相信完備且一致的數學體系指日可待。
哥德爾不完備定理敲碎美夢
不料第二年,大家的美夢就被一篇論文狠狠敲碎。才25歲的奧地利數學家哥德爾 (Kurt Gödel) 提出「哥德爾不完備定理」,證明任何一個基於算術公設的系統如果有一致性,就不是完備的,也就是其中一定有無法證明真偽的陳述(註二)。而且「哥德爾第二不完備定理」還指出:這個系統的一致性根本無法在系統內部獲得證明。

哥德爾正式宣判完備且一致的數學體系並不存在,追求聖杯只是徒勞,大家可以散矣。整個學界感到震驚與失落,正如馮紐曼的喟嘆:「一切都結束了!」。
如今希爾伯特的前兩個問題顯然答案都是否定的,而既然存在無法證明真偽的陳述,那麼第三個問題當然也就沒意義了。但能否退而求其次,把第三個問題改為:可否透過一套明確的程序判定某個陳述能不能被證明真假?也就是說,我們至少可以把這種無法證明真假的異類挑出來吧?
正是這個判定問題,讓圖靈跨入計算機的領域。
延續摯愛未竟之業——圖靈奮發向前的動力
圖靈於 1912 年在倫敦出生,到了中學就長得高大壯碩,還是長跑健將。不過他卻不是陽光男孩,相反地,他個性內向,在學校沒有多少朋友,其中最知心的是大他一個年級的莫康 (Christopher Morcom)。莫康因為感染肺結核,身體嬴弱削瘦,但他課業名列前茅,與圖靈一樣對數學、科學有極高的興趣,兩人常一起討論而成為莫逆之交。

圖靈對莫康愛慕不已,也因此才察覺自己的同性戀傾向。無奈莫康在畢業前一年不敵病魔而過世,用情至深的圖靈深受打擊,卻也因此更加專注於學業。他在寫給莫康母親的信上說:
「……我知道自己必須在學業上投注相同的心力,彷彿他仍然在世,因為他會希望我這麼做。」
圖靈如此努力的背後還有個重要動力。莫康原本已經獲得劍橋大學的獎學金,圖靈想替他實現未能完成的人生,以進入劍橋大學為目標,而最後圖靈也如願於 1931 年入學就讀。
1935年春季,圖靈在數學教授紐曼 (Max Newman) 的課堂上,聽到教授介紹希爾伯特的三大問題。紐曼提及修正後的「判定性問題」時,不知有心或無意,用的詞是「機械式程序」(mechanical process),而不是「明確的程序」。
機械式程序聽起來就是多了一層含意,暗示著一種不需人為介入的自動程序。而這層含意在圖靈心中埋下了種子,然後在初夏某一天的下午,圖靈慢跑完,躺在草地上休息時,想到了如何透過自動機器解決判定性問題。
圖靈機構造與運作原理
圖靈無意打造一台真正的機器,因為他要處理的是抽象的原則性問題,重點在於思辨過程,而不是加減乘除。因此圖靈只須設想這台自動機器如何運作,無需考慮它如何製造。事實上這台後來以他為名的「圖靈機」極為簡化,硬體組成只有一個可以左右移動的讀寫頭,以及一條無限長的紙帶。與其說它是計算機,反倒比較像是台打字機。
這條紙帶上面劃分成一個一個方格,每個方格只能打印一個符號。讀寫頭能掃描辨識符號、打印符號,或抹拭符號;它還能左右移動,但每次最多只能移動一格。讀寫頭的動作取決於它正下方那個方格內的符號,以及機器目前的狀態。這兩個參數也會決定讀寫頭每次做完動作後,機器狀態是否要改變。
這些影響讀寫頭與機器狀態的規則可以整理成一張「行為表」,例如下面這張:
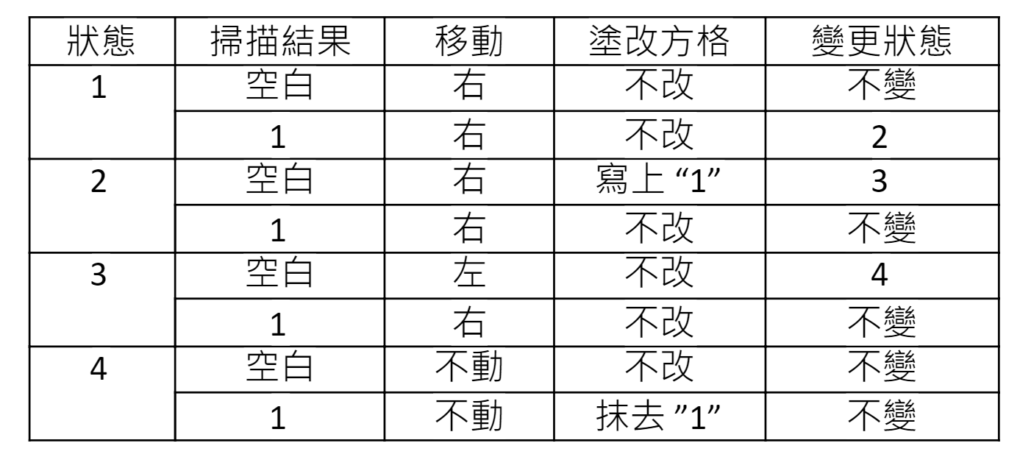
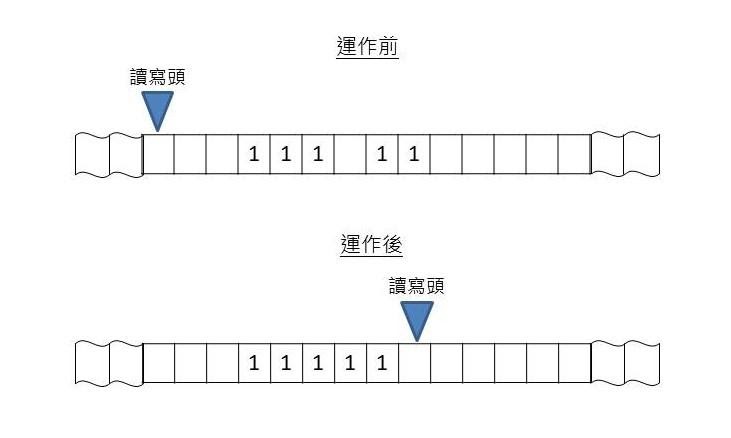
按照這張行為表,像下面圖中的紙條,原本3 個 “1” 和 2 個 “1” 彼此隔開,經過圖靈機後,就會變成 5 個 “1” 連在一起。我們可以當作這是 3+2=5 的計算,那麼配備這張行為表的圖靈機就是一台簡易加法器,可以任意加總兩個數目。
圖靈機構造再簡單不過,但只要在行為表中制定適當的規則,再複雜的計算,它都可以勝任。圖靈把可以透過有限的規則,讓圖靈機進行計算並以小數的形式印出來的數,定義為「可計算數」。
可計算數不一定是有限小數,像 1/3 = 0.3333……也算,反正紙帶無限長,或者你也可以決定小數點後幾位就停下來。因此像 √2、π 這種無理數也都是可計算數,因為它們可以用具有規律的無限級數表示(例如萊布尼茲所發現的 π/4 = 1 – 1/3 + 1/5 – 1/7 + 1/9 – 1/11 + ……),就能透過有限的規則,讓圖靈機計算。
描述數與通用圖靈機
不過圖靈機只能從紙帶上讀取資料,所以行為表得用一行符號來表達,才能印在紙帶上讓圖靈機掃描。例如上面那張行為表可能就會變成一行指令:
10RNN;11RN2;20R13;21RNN;30LN4;31RNN;40NNN;41N0N
接著我們把指令中的英文字母與符號用數字代替,例如 A ~ Z 改為 11 ~ 33,分號”;” = 99,數字也跟著改用兩位數 00 ~ 09表示。如此一來,指令就會化為一串數字,圖靈稱之為「描述數」,意指這行純數字的數列就能描述圖靈機的行為。
正常的描述數可以讓圖靈機經過有限步驟後停下來,產生可計算數。但某些描述數卻可能讓圖靈機中途動彈不得,或是不斷來回繞圈圈,無法產生有意義的答案。例如「讀到 1 就往右;讀到 0 則往左」這個指令,就會讓圖靈機遇到 “1”、”0”相鄰時左右來回,永不停止(這其實就相當於「說謊者悖論」)。
如果一台圖靈機只有一個描述數,我們當然可以輕易地發現某台圖靈機停不下來,從而知道這個描述數有問題。不過實際上不需要建造那麼多台圖靈機。想像有台特別的「通用圖靈機」(圖靈稱之為 ”Universal machine“),可以把其它圖靈機的描述數都掃描進來,那麼它便能模擬任何一台圖靈機的運作。而且描述數除了代表運作規則,也可以當成數字做為編號,按大小順序排列,方便圖靈機搜尋。
停機問題
現在問題來了,我們怎麼知道掃描進來的那麼多描述數之中,是否摻雜著造成圖靈機空轉的描述數?有沒有一套機械程序可以直接判定某個描述數能否讓圖靈機正常停機(而不用讓圖靈機實際執行,再看結果如何)?這就是所謂的「停機問題」。它的性質等同於希爾伯特的判定性問題:有沒有一套明確的程序可以判定某個陳述能不能被證明真假?
我們先假設真的有這麼一套判定停機與否的程序,那麼它可以把所有描述數的執行結果列表如下:(H代表會停機,N代表不會停機)
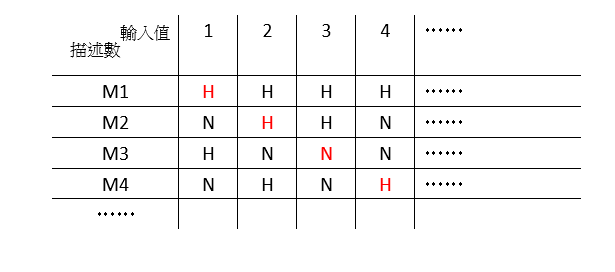
還記得上一篇介紹過的康托爾對角線法嗎?現在我們拿來如法炮製,可以編製一個新的描述數,輸入 1 的結果是 ”N”,與 M1 相反;輸入 2 的結果是 “N” 與 M2 相反;……以此類推。這麼一來,這個描述數絕對不在原來的表裡面,也就是出現判定程序不知其執行結果的描述數。
就算把這個新的描述數再納入表中也沒用,因為永遠都可以再用康托爾對角線法,新增一個不在表上的描述數。因此,根本不可能有套程序可以判定任一個描述數會不會停機。停機問題無解,代表數學上的判定性問題也確定無望,希爾伯特的三大提問至此可以休矣。(註三)
計算機不只會計算,還能模擬人的思考方式
1936 年 5 月,圖靈提交這篇影響深遠的論文:《論可計算數及其在判定性問題上的應用》 (On Computable Numbers, with an Application to the Entscheidungsproblem),不但在數學上占有重要地位,更展示許多計算機的創新設計。
他率先提出通用計算機的概念,將不同程式預先載入後再開始運行。而程式轉化為描述數,使得程式和資料共用同一個載體,也是首創。同時描述數做為程式的獨特編號,就相當於電腦程式在記憶體中的貯存位址;許多人相信這個概念啟發了馮紐曼用於 ENIAC 的設計。
圖靈還揭示了常人所未見的計算機角色。計算機的作用向來純粹就只為數學計算,但圖靈在這篇論文中卻是從人類如何思考的角度,討論如何讓機器模仿計算者的心智狀態。多年之後,圖靈提出「圖靈測試」,因而被稱為「人工智慧之父」,但其實這顆種子早在此時就已埋下了。
圖靈為了解決一個抽象的數學問題,而構思出通用圖靈機這台純屬想像的機器。幾年之後二次大戰爆發,這次為了千百萬人的生死存亡,圖靈將動手打造真正的計算機。
__________________________________________________________________________
註一:羅素設想有個集合 R 是由所有不包含它本身的集合所構成的集合。這定義感覺很撓口,但其實相當合理。因為在實際生活的應用上,幾乎所有集合本來就不包含本身,例如我們絕不會說昆蟲這個集合的成員包括昆蟲。問題來了,R 的成員應該包括它自己嗎?
如果說不應該,那麼 R 也是不包含自己的集合,所以 R 也應該屬於 R。但是這樣一來, R 就包含它自己,如此又不符合加入 R 的資格。結果不管 R 包不包含它自身,按照 R 的定義都會導致矛盾,這就是羅素悖論。
註二:算術公設指皮亞諾公設 (Peano axioms),是義大利數學家皮亞諾提出關於自然數的五條公設。
註三:其實美國普林斯頓大學的數學家丘奇 (Alonzo Church) 比圖靈早一個月,於 1936 年 4 月就提出論文,用正統的數學方法解決了判定性問題。圖靈獲悉後,也趕在論文發表前,在附錄處加註說明丘奇的證明。不過丘奇用的形式系統複雜多了,不如圖靈的方法簡單易懂,所以一般講到判定性問題的證明,都還是舉通用圖靈機為例。




































立體書封-300dpi-1.jpg)



