「數感盃青少年寫作競賽」提供國中、高中職學生在培養數學素養後,一個絕佳的發揮舞台。本競賽鼓勵學生跨領域學習,運用數學知識,培養及展現邏輯思考與文字撰寫的能力,盼提升臺灣青少年科普寫作的風氣以及對數學的興趣。
本文為 2019數感盃青少年寫作競賽 / 高中職組專題報導類佳作 之作品,為盡量完整呈現學生之作品樣貌,本文除首圖及標點符號、錯字之外並未進行其他大幅度編修。
作者:陳佳儀、葉又銘│臺北市立龍門國中

望故鄉
「葬我於高山之上兮,望我故鄉;故鄉不可見兮,永不能忘。
葬我於高山之上兮,望我大陸;大陸不可見兮,只有痛哭。
天蒼蒼,野茫茫,天之上,國有殤!」
2012年于右任的書法十四屏在北京銀座拍賣,以 747.5 萬元人民幣成交,創下了近代草書書法作品拍賣紀錄。于右任到底是誰呢?或許你曾到過鼎泰豐用餐,它的商號招牌便是在 40年前由創辦人向于右任求來的墨寶;又或許你曾看過許多國小大禮堂的「養天地之正氣,法古今之完人」的對聯;又或者台電帳單上的「台灣電力公司」字樣、行天宮、國立歷史博物館、東海大學等機關名稱題署,可說身邊處處有于右任的字跡作品。
被譽為當代草聖的美髯公于右任,書法藝術自成一家,也是當代標準草書的制定者。個性平易近人,很多人慕名前來求字,而他總是滿口答應,也不談金錢,瀟灑的揮毫、贈與,所以,才可以在全台各地發現他墨寶的蹤跡。那麼,問題來了,為何這樣一位注重名節、兩袖清風的溫和儒家長者,臨終前會寫出如此悲憤的詩句呢?
于右任是現今陝西咸陽市三原縣人,自幼便失恃,依親大伯母養育照顧,十歲進入私塾,而後苦學有成,年少時即被譽為西北奇才,並在十九歲時與夫人高仲林成親。于右任 25歲中舉後,理當可以在朝廷中謀得一官半職,過著安逸的生活,卻因悲憫飢民,作詩嘲諷時政而被通緝,流亡上海投入革命事業,成為孫中山的忠實追隨者,參與了無數次反抗清廷的革命與政變,是國民黨的元老級成員。之後於國共內戰時,因身為當時政壇及文壇領袖(監察院長及標準草書制定者),遭當時的蔣介石總統以為維持國民政府「正統」的名義,半強行挾持至台灣,渡海後因思念身在大陸的妻兒、親友,創作了許多有關思念故鄉的詩作與散文。其中,<望故鄉>是他將自己生前的渴望寄託在詩句之中,希望死後將他葬在高山之上,遙望中國故土。這次我們就是要探討,于右任在他所盼望的台灣最高的高山之上,是否見得到他朝思暮想的故鄉故土?若是見不到,他視線所及最遠又能到何地?
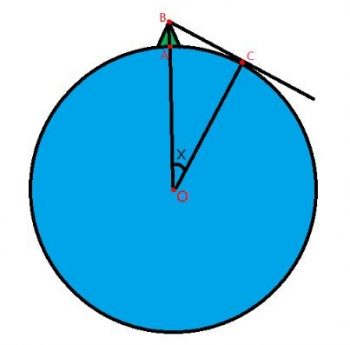
以地心O為圓心,地表至地心大略距離 6370km為半徑,玉山山底為A點,主峰峰頂為B點,並設可見最遠距離為C點,欲求弧AC之長度。線段AB為玉山高度 4km,加上線段AO(也就是半徑),使線段BO為直角三角形斜邊線,經B點作圓O的切線,交圓O於C點,以線段BC、線段CO為兩股長,形成直角三角形BOC,角BCO為直角。已知線段CO長 6370km,線段BO長 (6370+4) = 6374km,由畢氏定理可知線段BC長度約為 225.778653km。
再求X
\(\sin{X}=\frac{225.778653}{6374}=0.035422\)
\(X=\sin^{-1}(0.35422)=2.029956\)
弧AC長度為 2× 6370× 2.029956÷ 360= 225.6854km
從數學算式可以證實,于右任並不只是看不到他在陝西的故鄉而已,他的視線範圍連台灣海峽都跨不過去(玉山位處於南投信義鄉,離距離台灣最近的廈門市都有 308公里左右)。
事實上,詩人最終沒有埋骨在玉山遠望家鄉,而是葬在陽明山,而當時政府立於玉山的于右任紀念銅像,也在 1996年被毀損。也許已故去的右老並不在乎這些,于右任一生寫下千餘首詩篇,從年少時意氣昂揚的「書生報國無他物,唯有手中筆如刀」。在臺灣居閒職時,對當時執政者蔣經國先生的期許「計利當計天下利,求名應求萬世名」。和對遙遠故鄉結髮妻子的懷念「白頭夫妻白頭淚」。我們上幾代的許多長輩們即使流落異鄉也難以忘懷孕育自己生長、付出青春熱血和理念的土地。這是時代的悲劇,但是對鄉土國家的依戀,一直是于右任詩中的精神魂魄。在數學學理與現實中「故鄉不可見兮」、「大陸不可見兮」,然而他詩句中卻仍然寫下「葬我於高山之上兮」,即使看不到,仍然盼望著近一些、再近一些,再讓自己的視線放遠一點,望其故鄉、望其大陸、願其——歸鄉。