本文為系列文章,上一篇請見:搞懂「通用圖靈機」的終站——它的誕生與意義 │《電腦簡史》數位時代(十三)
奇謎機
1938 年 6 月,圖靈以不到兩年的時間,在普林斯頓大學取得博士學位。馮紐曼有意留他下來當研究助理(與電腦無關,此時馮紐曼對電腦還沒產生興趣),但圖靈放棄這個工作機會,選擇返回母校劍橋大學擔任研究員,打算之後再申請教職。不料才過了一年,「政府代碼及密碼研究院」(Government Code and Cypher School) 就徵召他為國效力。
顧名思義,這個部門就是專門破解各種加密的情報。以往的加密方式都是以人工參照密碼表,將原來的字母改用別的符號代替,變化有限,還可以用腦力推敲破解。不過從 1920 年代開始出現機器加密,複雜度大增,越來越不容易破解。尤其德軍所用的「奇謎機」 (Enigma,也譯為「恩尼格瑪機」),更是令人束手無策。

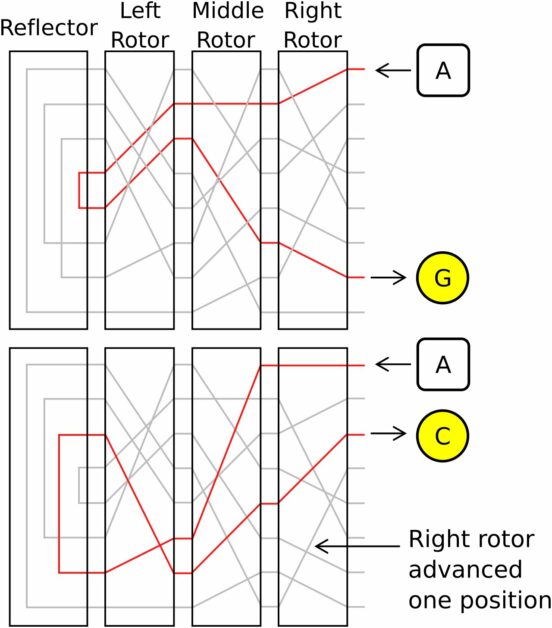
奇謎機約一台打字機大小,主要靠三片轉盤與一個反射器變換字母。三片轉盤彼此相扣,每片都有 26 個金屬接觸點代表不同字母;在鍵盤上輸入字母後,訊號經過三片轉盤抵達反射器,再從這三片轉盤走不同路徑返回,變換成另一個字母。每輸入一個字母後,第一片轉盤便轉一格,轉完一圈即帶動第二片轉盤轉一格,然後第二片轉盤也是如此帶動第三片轉盤。
這個設計可以讓同一個字母每次都置換成不同字母,看似毫無規律,難以破解。而且每天調換三片轉盤的位置,所以一共會有 26 x 26 x 26 x 6 = 105,456 種電路變化。加上德軍又多設了類似電話交換機的接線板,可以任意讓兩個字母互換,任選 6 組就有一千億種組合,使得所有變化的可能性達萬兆以上,可以說沒有破解的可能。不過法國的情報人員於 1932 年取得接線板 9、10兩個月的設定指示,為破解工作開啟了契機。
波蘭人
其實就算掌握了接線板的接法,要破解轉盤的十萬種電路變化,仍是件不可能的任務。當時希特勒才剛掌權不久,尚未暴露侵略野心,而英、法兩國又都認定德國軍備受到凡爾賽合約限制,因此都沒有認真對待這份奇謎機的情報。反倒是波蘭過去的亡國之恨記憶猶新,如今左右兩旁的德國與蘇聯仍虎視眈眈,因此非常積極的研究這份情報,試圖破解德軍的加密系統。
所幸德軍也自恃奇謎機無法破解,竟將當日的轉盤初始設定置於電報開頭,而且重複兩次,例如三個轉盤分別設在 B、T、F 的話,就將 ”BTFBTF” 加密,可能變成 “RCOMIA”。德軍認為這麼做萬無一失,但波蘭學者經由大量比對德軍電報,還是找出其中規律,推敲出奇謎機的運作方式。
他們於 1938 年造出模擬奇謎機的「炸彈機」(Bomba,波蘭文炸彈之意,因為運作起來滴答作響,有如定時炸彈),共有六台,各代表轉盤六種排列組合中的一種,然後讓它們同時運作,再挑出符合電報內容的一種。
布萊切利莊園
可惜才過一個月,德軍於 1938 年底又多加了兩片轉盤,變成從五片中任選三片,共有 60 種可能組合。同時接線板互換的字母也從 6 組變為 10 組,使得變化高達 1.5 億兆。原來的炸彈機已派不上用場,波蘭束手無策,只得向盟國請求合力破解。
無奈破解之道尚無頭緒,德軍就已經在 1939 年 9 月閃電入侵波蘭。英、法兩國直到此時才大夢初醒,正式向德國宣戰,同時徵召包括圖靈在內的許多數學家進駐布萊切利莊園 (Bletchley Park),努力破解奇謎機。雖然波蘭人的研究成果讓他們不必從零開始,但若不能把天文數字般的可能組合縮小範圍,一切仍是枉然。
所幸實際上並沒有那麼多變化。因為同一部奇謎機除了加密,也要解密收到的訊息,所以同樣狀態下,若 A 加密為 S,則輸入 S 也會轉成 A;而且每個字母一定不會加密成本身,也就是祕文中的 A 在原文絕對不是 A。這就減少了許多可能性。另外,德軍的有恃無恐再次留下破口,他們沒料到電報中固定出現的「天氣」、「希特勒萬歲」等關鍵字成為破解的線索。
圖靈的炸彈機
圖靈從這些基礎出發,運用數理邏輯排除更多不可能的組合,然後把測試比對的工作轉化成機械程序,設計出英國自己的炸彈機 (Bombe)。1940 年 3 月,第一部原型機完工,高、寬各約兩米,有 108 個輪鼓,每 3 個一組,模擬 36 種奇謎機轉盤的組合。兩個月後,炸彈機首度破解德軍的加密訊息,雖然是幾個星期前的情報,已經沒有軍事價值,卻足已證明圖靈的設計可行,只不過需要更強大的計算能力。

8 月,團隊中的另一位數學家魏奇曼 (Gordon Welchman) 設計出「對角線板」,針對字母兩兩配對的特性,自動排除不需要的嘗試,大幅縮短破解的時間。於是隨著更多部加裝對角線板的炸彈機上線運作,破解德軍電報的效率逐漸提高,到了 1941 年中,已經可以在 36 小時內解譯出電報內容。
這對英國的存亡極為重要,因為此時美國仍保持中立,尚未派軍到歐洲戰場。英國艦隊與補給船屢屢被德國潛艇攻擊,卻一籌莫展,情勢越來越危急。如今破譯了德軍的通訊內容,得以掌握其軍事佈署,終於能避開潛艇攻擊,延續國家元氣。
不過從 1942 年 2 月開始,炸彈機突然怎麼樣也無法正確算出奇謎機的設定。原來德國海軍察覺有異,於是在奇謎機上又多裝了一片轉盤。所幸這第四片轉盤是固定的,無法抽換,所以電路的變化只有原來的 26 倍。只不過目前布萊切利莊園已經是用 30 部炸彈機在處理,哪有能力再重新設計,而且得生產出 780 部!
美國之行
英國不得不尋求美國協助,但就得將布萊切利莊園的研究成果與美軍分享,才能讓美國同意幫忙製造炸彈機。於是圖靈奉命於 11 月前往華府,傳授相關技術細節,並協調英美雙方如何共同打造炸彈機。
圖靈此行還肩負另一項任務:開發語音加密的技術。除了電報,有更多的溝通協調、下達命令、……等等,是透過電話進行。為了避免重要機密遭敵方竊聽,勢必也要對語音加密才行。
對於加密/解密已相當熟稔的圖靈當然是第一人選,而美國的貝爾實驗室則是電話系統的龍頭廠商,雙方若能攜手合作必能事半功倍。因此圖靈結束華府的協調工作後,即於 1943 年 1 月轉往紐約的貝爾實驗室。
圖靈並不知道此時貝爾實驗室的史提畢茲正在打造內插值計算機,這是美國第一部可程式化的數位計算機,圖靈肯定會有興趣。可惜貝爾實驗室組織龐大,不同專案有各自的隔間,圖靈在這裡待了兩個月,竟然沒有與同一棟大樓中的史提畢茲認識,否則不知會蹦出怎樣的火花。

與夏農的每日茶敘
不過圖靈倒是結識了電腦史上更為關鍵的人物,那就是與他有許多共通之處的夏農。夏農與圖靈相差四歲,兩人都有開創性的真知灼見,也都有計算機的實務經驗。
1936 年,圖靈在〈論可計算數〉這篇論文中,揭示了通用計算機的基礎架構;此時夏農正在 MIT 操作微分分析儀。1937 年,夏農在他的碩士論文中首創邏輯電路的理論基礎;此時圖靈也在普林斯頓打造了簡單的二進位電子乘法器。而當圖靈在布萊切利莊園努力破解德軍密碼時,夏農也正從密碼學出發,發展影響深遠的「資訊理論」(他曾指出:「密碼其實和帶有雜訊的通訊系統相去不遠。」)。
由於戰時嚴格的保密規定,圖靈不得透露關於布萊切利莊園的一切,但這無礙於他與夏農很快發現有共同興趣,且彼此心智相近而惺惺相惜。他們幾乎每天下午茶的時間,都在貝爾實驗室的自助餐廳碰面討論電腦的可能性。圖靈分享他論文中的通用圖靈機,夏農更是大膽提出將音樂之類的文化事物輸入電腦,兩人大談機器能否模仿人類大腦運作。
當時電晶體都還沒發明,但圖靈的機械程序與夏農的邏輯電路,都是超越技術層面的普遍性原則,因此他們兩人於 1943 年 1 月中到 3 月中這兩個月的交鋒,應該是史上首次針對人工智慧的論辯。七年之後,圖靈將提出區辨人機的「圖靈測試」,夏農則提出如何教電腦下棋,還打造了一隻走迷宮的電子老鼠。
「魚」與「巨像」
在圖靈來美國出差前幾個月,當年啟發他想出圖靈機的老師紐曼也加入布萊切利莊園。這是因為柏林最高指揮部於 1942 年中開始使用另一套基於二進位的加密系統與陸軍聯繫,炸彈機派不上用場,英國急須開發另一部二進位的計算機,以破解這套暱稱為「魚」的加密系統。紐曼便因其數學專長而被招募進來領導研發工作。
第一代原型機於 1943 年 1 月開始建造,但 2 月德軍又提升「魚」的複雜度,以致機器還未造好就已過時。若要及時破解新的加密系統,計算機的運算速度必須大幅提升,而這唯有用真空管取代繼電器,完全用電子訊號運算才可能做到。於是紐曼團隊著手打造全新的計算機「巨像一號」(Mark 1 Colossus),由來自英國郵政總局的工程師弗勞爾斯 (Tommy Flowers) 負責設計。
圖靈雖然一開始沒有參與設計,但巨像一號是沿用他在出差美國之前,所建立的數學模型,所以當圖靈於 1943 年 3 月返回布萊切利莊園後,除了繼續研究語音加密,也同時擔任巨像團隊的諮詢顧問。
巨像一號於 1943 年底完工,共用了 1,600 個真空管,資料以打孔紙帶輸入,還能透過切換開關與纜線設定不同程式,成為史上第一台可程式化的數位式電子計算機。果然,諾曼團隊於 1944 年 2 月便開始破解「魚」的訊息。他們繼續打造速度快五倍的「巨像二號」,及時於 6 月 1 日上線破解德軍情報,盟軍才能於 6 月 6 日發起諾曼地登陸,成功展開決定性的一役。

打造馮紐曼架構之電腦
二次大戰結束後,布萊切利莊園立下大功的成員默默回歸原來的工作崗位或教職,但圖靈沒有回去劍橋大學,而是被「國家物理實驗室」(National Physical Laboratory) 延攬。原來實驗主任收到馮紐曼的〈EDVAC 報告初稿〉後,決定要根據裡面建議的馮紐曼架構,開發英國自己的通用型電腦 ACE (Automatic Computing Engine),因而找上兼具理論與實務經驗的圖靈。
〈EDVAC 報告初稿〉提到他們美國團隊採用自己開發的水銀延遲線做為記憶裝置,問題是國家物理實驗室並沒有這樣的工程團隊,圖靈只能找曾一起在布萊切利莊園共事的弗勞爾斯幫忙開發水銀延遲線。但弗勞爾斯已回郵政總局,須優先處理電信網路事宜,無法全力配合。眼見 ACE 的進度延宕無解,深感挫折的圖靈終於在 1947 年中求去。
在此同時,被延攬至曼徹斯特大學的紐曼也有意打造新一代電腦。他與馮紐曼本為舊識,於是主動向他索取〈EDVAC 報告初稿〉,也爭取到英國皇家學會贊助研發經費。紐曼還找回當初巨像團隊的部分成員,另外特別招募威廉斯 (F. C. Williams) 加入,因為他所發明的「威廉斯管」(Williams tube) 更勝水銀延遲線。
威廉斯管利用陰極射線管的電子束打在螢光幕上所產生的電荷變化,代表 0 與 1 來記錄資料。這種方式寫入與讀取資料的速度比水銀延遲線快非常多,而且還可以隨時存取任一區塊的資料,省卻等待的時間。

曼徹斯特一號
1948年中,簡化版的先導機型「曼徹斯特寶寶」(Manchester Baby) 完工。它雖然暱稱為寶寶,卻是個長 5.2 公尺、高 2.2 公尺,重達一噸的龐然大物;不過如果把僅有 550 個真空管與 1,024 位元的記憶容量看成大腦,倒是蠻名符其實的。 6 月 21 日,曼徹斯特寶寶成功執行了一個 17 行的程式,算出 218 的最大因數,不但驗證了威廉斯管的可行性,也成為第一部預存程式的數位電腦。
紐曼請圖靈寫第二支測試程式,順便藉此邀他一起來打造完整版的「曼徹斯特一號」(Manchester Mark 1)。圖靈答應了,不過電腦的整體架構已大致底定,沒有多少空間讓他發揮,他便負責設計程式及編寫《程式設計師手冊》。
曼徹斯特一號於 1949 年 4 月成功上線,直到 1950 年 8 月技轉給英國政府支持的弗蘭提企業 (Ferranti) 後,功成身退。圖靈也未再涉足電腦的設計開發,而是將興趣轉向胚胎學的研究。心智與生命是人類的兩大奧秘,他可以用機械程序描述心智的運作,現在他也想找出胚胎分裂生長的背後法則。

模仿遊戲
1950 年 10 月,哲學期刊《心智》(Mind) 刊出了圖靈的論文〈計算機器和智能〉(Computing Machinery and Intelligence)。這是他在參與曼徹斯特一號的開發時,閒暇之餘重拾電腦與心智的思辨,所寫成的論文;著名的「圖靈測試」便是源自於此。
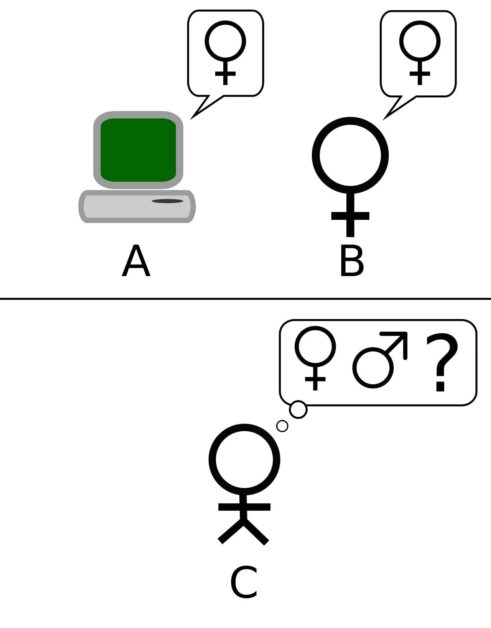
文章開頭便問:「機器能思考嗎?」要回答這個問題得先定義「機器」與「思考」,但既然很難有共同認可的明確定義,圖靈提出一個猜測性別的模仿遊戲來檢視這個問題。這個遊戲由一人扮演審訊員,他要猜出隔壁房間的兩個人誰是男性、誰是女性。審訊員可以問他們任何問題,女性一定會誠實回答;男性則會假冒女性,設法欺騙審訊員。他們的回答都是透過電傳打字傳遞出來,所以審訊員只能從文字內容做出判斷。
現在,把這位男性換成一部機器的話,機器也能騙過審訊員嗎?用這個問題取代「機器能思考嗎?」,就可以有明確的判斷標準了。後來圖靈在 1952 年 1 月播出的對談節目中,把模仿遊戲簡化為電腦要設法讓審訊員相信它是真人,這就成為現今判別人工智慧程度的圖靈測試了。
圖靈之死
這個廣播節目播出後過了九天,圖靈的住處遭竊。警方很快從指紋查出一名慣竊,原來他認識圖靈於耶誕節前才在街頭邂逅的男友,才來闖空門。他在偵訊過程中告訴警方圖靈與他朋友的性伴侶關係,圖靈因此以嚴重猥褻罪的罪名遭到起訴。
圖靈同意接受治療以換取緩刑,而所謂治療就是注射荷爾蒙以消弭性衝動,結果他不但變成性無能,還長出胸部。但圖靈似乎若無其事的繼續他的生物研究,直到 1954 年 6 月 8 日——他 42 歲生日前兩週,被發現死於家中,死因是氰化物中毒。
究竟圖靈是蓄意自殺,或是如他母親認定的是做實驗不小心誤食的意外?圖靈死前的確沒有任何輕生的徵兆,也沒留下遺書,然而他卻在 2 月時特地立了新的遺囑。此外他在床頭留下那顆咬了幾口的蘋果,不禁讓人想到他喜愛的迪士尼卡通《白雪公主與七矮人》中的場景,不過警方並未做化驗,無從得知蘋果是否塗了氰化物。
無論如何,除了他的朋友同事感到震驚,圖靈的死訊在外界卻是波瀾不興。由於英國政府堅持保密,外界仍不知道是布萊切利莊園團隊破解了德軍密碼,自然也不知道圖靈間接拯救了多少生命。
〈論可計算數〉這篇重要的論文被歸為數學領域,只有少數人看出它在電腦發展上的重大意義。「模仿遊戲」在電腦才剛起步的當時,更只像是空想的哲學思辨,無關乎真正的電腦。而外界所知的電腦中,曼徹斯特一號並非由他主導,他一手設計的 ACE 電腦後來又由別人接手完工,光環全不在他身上。
遲來的正義
1966 年,「計算機協會」(Association for Computing Machinery) 終於設立了「圖靈獎」以紀念他的貢獻。至於他在二次大戰的功績,要到 1970 年代才為世人所知。2009 年,在超過三萬人的連署請願下,英國首相終於代表國家對圖靈當年因同性戀所受的刑罰公開道歉;但他的罪名要到 2013 年底,才由英國女王正式宣布赦免。

回頭來看,英國政府於 1952 年將圖靈判刑的這一年,恰巧也是英國電腦發展落後美國的分水嶺。從巨像、曼徹斯特、ACE,乃至弗蘭提,這一系列電腦原本都還領先美國,但是自從馮紐曼的 IAS 與摩爾電機學院的 EDVAC 分別於 1952 年的 1、2 月啟用後,英國就被遠遠拋在後頭了。自此,無論是技術層面或是實際應用,整個電腦產業盡由美國所主導。