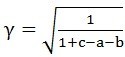作者:豬文
舊世紀福音:「神用六天創造了世界,我們的祖先在那裡活得幸福快樂。但有天,他們受不住引誘,吃了禁果,所以我們都有原罪。我們都有原罪,所以我們的一生就是一個救贖的過程。上帝派了祂的兒子到這個世界,為我們犧牲,所以我們都得到救贖。」
隨着人類文明的發展,尤其是科學的進步,這個關於原罪、福音與救贖的故事愈來愈少人相信。對很多人來說,這只是人類歷史中,一個曾經使人痴狂著迷的故事。它已經是一個舊世界的福音故事。那麼,活在「新世紀」的我們,還有原罪嗎?我們仍需要救贖與福音嗎?
「需要。」《新世紀福音戰士》的監制庵野秀明這樣說。
活在「新世紀」的我們,仍然有一種無法擺脫的「原罪」。但又有誰能救贖我們呢?我們期盼着的新世紀福音又是什麼?人類為什麼需要補完?又如何能夠補完?或許《新世紀福音戰士》便是講這樣的一個故事。
或許是害怕孤獨吧
新世紀的人,不再相信自己都是上帝的兒女,不再相信身邊的人都是自己的弟兄姊妹,不再受亞當夏娃的羈絆所牽扯。我們成為了新世界的主人,每個人都是獨立、自由、自主。不用神之子,我們早已救贖了自己。但新世紀的我們,就此過回當初亞當夏娃的美滿生活嗎?似乎新世紀的生活並沒有變得美好,我們依舊活在絕望、痛苦與恐懼之中。那麼,我們到底在害怕什麼?
似乎新世紀的生活並沒有變得美好,我們依舊活在絕望、痛苦與恐懼之中。圖/動畫截圖
當上帝跟我們的羈絆、人類祖先跟我們的羈絆,以至我們彼此的羈絆都失去的時候,我們就是一個個孤懸的個體。活在新世紀的人,最害怕的是寂寞、是疏離、是自己孤獨的存在。
因此,我們都需要他人。無論快樂與憂愁,我們都需要和別人在一起 。一個人的快樂,彷佛不是快樂。一個人的憂愁,像是兩倍憂愁。為了打開那度與人連在一起的窗,人類瘋狂地發明了無數「社交」工具:Facebook、IG、Whatsapp、Line、Skype,為的就是使我們可以無時無刻地與別人在一起。只要我們願意,我們孤獨的「原罪」必會得到救贖,就像舊世紀裡的福音一樣。
外表堅強的明日香,曾經以為自己可以獨自一人活下去。source:IMDb
外表堅強的明日香,曾經以為自己可以獨自一人活下去。她相信,即使爸爸不在、媽媽不在,她也可以活得好好的。但她真的能做到嗎?她真的抵受到寂寞隨時隨地的來襲嗎?無論她外表多堅強,到頭來,還是會因為寂寞而哭。
努力逃避一切人際關係的葛城美里,也無法真正孤獨地活著。source:IMDb
努力逃避一切人際關係的葛城美里呢?她也無法真正孤獨地活著。無論她多努力收藏自己,她還是需要別人。對着加持良治、赤木律子、碇真嗣,美里總有些時候會忍不住敝開自己的心,哪怕只是扇敝開一瞬間很快又閉回去的窗。
別人於我的意義,除了是心理上的慰藉之外,還有行動上的意義。以真嗣為例,他人為真嗣提供了一種生活方式:每事隨大眾而活。大眾不是一個具體的人,只是眾多的他人所組成面目模糊的東西。但這個面目模糊的東西卻有種力量,可以對我的生活指手劃腳。我甚至可以把整個生命交託給「它」。
碇真嗣一直也在過這種毫不費力的生活。別人要他駕駛 EVA,他便駕駛 EVA,別人因此稱讚他,他便更投入在駕駛之中,甚至把駕駛 EVA 當成了自己整個生命的基礎。當別人託管了碇真嗣的生活之後,真正的碇真嗣便不用再為自己的生活費煞心神。在明日香眼裡,這種交托給大眾的生活「本身就是一種輕鬆的生活方式」。
當別人託管了碇真嗣的生活之後,真正的碇真嗣便不用再為自己的生活費煞心神。source:IMDb
因此,當真嗣發現自己在一個只有自己沒有他人的世界時(第廿五話),他立刻感到手足無措。只能說「告訴我到底該怎麼辦好」。或許,你會覺得真嗣這種完全依賴他人的生活方式,太過極端,並非一般人的處境,但我們仔細省視一下自己的生活,他人仍然是極其重要。
設想一下,世界上所有人都消失了,只剩下你一個,有多少人仍然會做現正手頭上在做的東西?有多少人還知道自己的人生目標?我們在思考要做甚麼不做甚麼時,他人總是像個拿不掉的背景,是我們行動時潛而不顯的前提。即使你沒有把生命假手於人,我們絕大部分所做的事也唯有他者存在才有意義。
像以前的人由上帝引領一樣,我們現在也可以把自己交由大眾引領,免去思索自己下一步要去哪裡的痛苦。沒有了他人作為我生活的背景,沒有了大眾作為我的牧羊人,是多麼可怕的一件事。因為沒有了他人,我們都不知道能到哪裡去。
他者存在甚至是我存在的先決條件。 沒有他人,我便無法能把「我」這個東西的界線劃出來。我把「我」這個東西的界線劃出來的一瞬間,他者也同時被劃分出來了。這就像你在一無所有的白紙上劃出第一個圓形,圓形存在的同時,不屬於這個圓形的東西也存在了。佛家說,這個狀態「如兩束蘆,互倚不倒」 (《雜阿含經》)。你我就像兩根蘆葦,你依著我,我依著你。拉走任何一邊,另一邊都不可能站得住。[1]
只要你是一個人,而不是 AT 力場強大的使徒,你就不可能孤獨地活着。source:Pascal
我們心理、行動、存在上都需要他人。對軟弱的碇真嗣如是、冷酷的綾波零如是、外表堅強的明日香如是、成熟能幹的葛城美里如是、甚至為求目的不擇手段的碇源堂也如是。只要你是一個人,而不是 AT 力場強大的使徒,你就不可能孤獨地活着。
也或許是害怕他人吧
「我們無法獨自存在」只是整個新世紀原罪故事的一半。因為如果童話中,「兩人永遠幸福快樂地活下去」的情節是真的話,「我們無法獨自存在」這個宿命根本沒甚麼大不了。可是,我們都知道「兩人永遠幸福快樂地活下去」只是騙人的幻想。這從來都不可能。你我除了是兩束蘆葦,更像兩把利刃。兩個人走在一起,總有互相撕磨的一天。
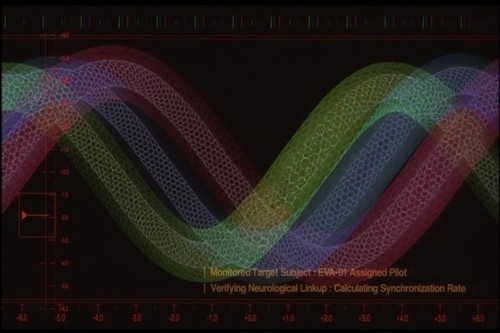
在整個《新世紀福音戰士》的故事中,同步率是個永恆的問題:同步率100%永遠只是個短暫的僥倖。
在整個《新世紀福音戰士》的故事中,同步率是個永恆的問題:同步率100%永遠只是個短暫的僥倖。source:動畫截圖
你與我之間的關係是如此脆弱,我們的存在也是如此脆弱。在渴求他人的過程中,我們總是如此害怕。我們害怕別人討厭自己,害怕別人不再需要自己,害怕別人離自己而去。在與他人相處的時候,我們總是提心吊膽,總是禁不住猜度別人眼中的自己。甚至,我們會成為了一個只為了討好他人而活的人。碇真嗣喜歡駕駛 EVA 嗎?凌波零喜歡嗎?明日香喜歡嗎?根本沒人喜歡。碇真嗣討厭碇源堂,但也怕被他討厭。怕被他討厭,因為怕被他拋棄。怕被他拋棄,因為碇真嗣是人。
碇真嗣討厭碇源堂,但也怕被他討厭。source:IMDb
明日香時常想勝過他人,因為她想被別人需要。她想被別人需要,因為她知道她的爸爸、媽媽都不再需要她。如果沒有人再需要她,她也沒有存在的理由。
明日香時常想勝過他人,因為她想被別人需要。如果沒有人再需要她,她也沒有存在的理由。圖/動畫截圖
的確,像明日香所說,把生命交託給別人,是一種輕鬆的生活方式。但這也意味著我的生命已經不再是自己的。一個不是自己的生命,無論是個多麼出色的 EVA 駕駛員,又有甚麼意義呢?
在一個只有自己的世界裡,就像碇真嗣所說,總等待他人可以「告訴我該怎麼辦才好」。但這個不知接下來要做甚麼的世界,也是一個做甚麼都可以的世界。我不知道要做甚麼,正正是因為我似乎甚麼都可以做。也就是說,沒有他人的世界,才是一個真正自由的世界。
在這個只有我的世界裡,我是一切的主宰,一切的中心。世上的一切都在黑暗裡靜靜地待着,我是唯一可以照亮他們的光。只有我能把它們從寂靜之中喚醒,使它們的存在變得有意義。整個世界裡,只有我有權,去評價它們,去喜歡或厭惡它們,去親近或拋棄它們。[3]
如果我想生火,我隨手拿起一根樹枝,這根樹枝便是燃料。但如果我想爬山,它便成為了一根手杖。如果我既不想生火又不想爬山,它便只會繼續躺在路邊,在黑暗中待著。世上的一切,它們的意義、價值的高低,都由我一人說了算。我「統治」著這個世界。我是自由的。
在這個只有我的世界裡,我是一切的主宰,一切的中心。我「統治」著這個世界。我是自由的。圖/作者提供
但當他人走進來了之後,一切都改變了。他人破壞了這個自由的世界。這就像這部只有我一個人做主角的電影,突然多了另一個主角。更可怕的是,我知道我在這個「另一個主角」的眼中,就只是一個配角,正如他在我眼中永遠不可能是主角。我在他的眼中,就像他在我眼中一樣,只是一個被我所評價、喜歡或厭惡、親近或拋棄的一個對象。
沙特有個有個著名的故事,可描述這個經驗。設想,某酒店房間傳來一陣聲音,好奇的我透過房門的鑰匙孔去偷看房間發生的事情。這個時候的我,是世界唯一的觀察者。即使我是在偷窺,我也不會感到羞恥。因為我根本沒有意識到自己可以被評價,成為一個被引以為恥的對象。突然,一個酒店的員工站在我背後。我回頭一看,看著他正看著我。羞恥的感覺一瞬間便充滿了我的身體。我立即開始為自己的行為解釋。
我所說的一切,一舉手,一投足都被他人看在眼裡,成為他人評價的對象。圖/作者提供
這個經驗說的是,在只有我的世界,我是賦予意義的主體,也是世界的中心。但他人闖進來之後的世界,我成為了被評價的客體,也放逐到世界的邊緣。突然,我不再自由了。我所說的一切,一舉手,一投足都被他人看在眼裡,成為他人評價的對象。當我意識到這點之後,我便會為自己感到羞恥,亦感到要向別人交待的壓力。沒有他人的話,我又怎會無端為自己偷窺的行為作個解釋?又怎會無端為偷窺的自己感到羞恥?
當他們意識到自己不如別人所期望時,他們都為自己的存在感到羞恥,甚至寧願自己從不存在。圖/作者提供
因為不想再被人視為懦弱,所以碇真嗣強迫自己勇敢。因為不想被人視為無用,所以明日香強迫自己成為最出色的人。當他們意識到自己不如別人所期望時,他們都為自己的存在感到羞恥,甚至寧願自己從不存在。
而且,我與他人的相處永遠在矛盾之中。因為他人作為世上除我以外的主體,挑戰了我對世界的「統治權」。我本來自由地「統治」着世界,世界的一切意義都是我所賦予的。但當我意識到世上還有其他評價者時,我便發現,我對事物的意義根本沒有控制權。我與他人的相處,其實就是在爭奪意義的話語權。
當疲倦的我走向眼前一張長椅,我看到的是一個可以好好休息的地方。但對從另一邊走過來的上班族來說,他看到的是一個可以用來吃午餐的地方。我們都是「統治者」,但我們卻生活在同一個世界。我們共同的事物經驗,卻各自賦予事物不同的意義。一張公園長椅的意義可能沒甚麼大不了。但他人與我所爭奪的,也可以是某個人的意義,甚至我自己的意義。這些意義的爭奪,便是為甚麼人與人永不可能「和平」共處的原因。
因為他人,所以我永遠活在彷徨之中、所以我失去了屬於自己的生命、所以我恥於自己的存在、所以我要向他人交待、所以我失去了對世界的「統治」而變得不自由。但我們能夠逃回去那個只有自己的世界嗎?No Exit。
新世紀的原罪便是:我永遠需要與他人活在一個沒有出口的房間,但他人永遠是個地獄。 [2](電視版《新世紀福音戰士》的第 25、26 話可能是日本動畫史上最令人錯愕的結局。從劇情的角度看,這個「結局」無疑是令人無言的,但其實這兩話透過一種意識流的手法,表達了整個故事的核心:新世紀的原罪。)
新世紀福音與救贖
這個讓人絕望的存在處境,便是新世紀的原罪。
人類有原罪,所以我們需要救贖,也就是——人類補完計劃。
source:satwoon
人類如何才能補完?對 SEELE 來說,便是解放全人類的絕對領域,打破人與人之間的隔膜,使一切個體都融合在一起,回歸成一片 LCL 之海。這便是我們的救贖,新世紀的福音。在這片 LCL 之海中,不會再有憎恨、不會再有拋棄、不會再有不自由、不會再有羞恥、不會再活不下去。因為這裡連他人也不再有,你就是我,我就是你。
這是我們唯一的補完計劃嗎?對碇真嗣的母親碇唯來說,這個不是真正的新世紀福音,因為沒有了有如地獄的他人,也等於沒有了自己。碇唯認為,SEELE 的計劃,與其說是你中有我,我中有你,不如說是沒有你也沒有我,一切歸於虛無。
所以碇唯走的是另一個極端:若果我們不能「打成一片」,倒不如使人類可以強大得有如使徒般活著。所以她製造了一種可以寄存人類靈魂的 EVA 機。EVA 機的參照原型正是 AT 力場強大得可以孤獨地活著的使徒。如果我們可以像使徒強大,不用依賴他人的存在而活的話,我們的原罪也一樣能夠被救贖。
這便是碇唯心中另一個方向的人類補完計劃。
「真令人受不了」
一切歸於虛無,還是永遠孤獨地活著?意外成為「上帝」的碇真嗣,在最後放棄了這兩個選項。他選擇了原本的世界。沒錯,這個與他人困在一起的世界就是個地獄。碇真嗣在選擇完之後,看到明日香這個他者的一瞬間,便痛苦得想挬死她。這個有你有我的世界,就如全劇最後一句對白所說:「真令人受不了」。
這個與他人困在一起的世界就是個地獄。碇真嗣在選擇完之後,看到明日香這個他者的一瞬間,便痛苦得想挬死她。圖/作者提供
但也唯有這個有你有我的世界才會有愛與感情。沒有了他人、沒有了恨,也不會有愛。他人就是地獄,但也唯有他人,這個世界才會如此精采。沒有了他人,就不會有朋友、親人和愛人。 所以,碇真嗣放棄了「救贖」,回到這個充滿了人與人的世界,回到他人的地獄裡。每天緊緊地夾在他者之間的你,又同意碇真嗣最後的選擇嗎?
碇真嗣放棄了「救贖」,回到這個充滿了人與人的世界,回到他人的地獄裡。圖/作者提供
後記
source:IMDb
說《新世紀福音戰士》這套動畫是神作,應該不會有太多人反對。[4] 即使你沒有看過《新世紀福音戰士》,你也會聽過凌波零、暴走、使徒這些東西。不過,與它受歡迎程度成正比,正是其晦澀程度。
它之所以是一套極難懂的作品,因為一方面,撇開這套作品所探討的主題與所包含的哲學意涵,這套作品的故事情節本身就已極其難懂。大量世界觀設定都沒有明確交待過。至少,我在第一次看這套動畫的時候,連使徒是甚麼、為甚麼要跟使徒戰鬥也是完全沒有搞懂。一口氣看完廿十多集後,只記得看了一堆超有型的 EVA 機在暴走。
source:IMDb
另一方面,這套動畫用了一大堆宗教符號及疑似科學術語。甚麼死海文書、亞當、S2 機關、迪拉克之海(迪拉克 Dirac 是二十世紀的一位英國物理學家),每每看得人頭昏腦脹。在這些宗教與科學符號的迷霧下,《新世紀福音戰士》的故事便變得更撲朔迷離,更不用說它所包含的哲學意涵。
關於宗教與科學符號的部分,個人認為只是一種文學的修辭手法,用以渲染整套作品的神祕氣氛,對我們理解整套作品來說,不太重要(當然,正如第一節所說,此作品探討的主題與整部聖經的主題是有相通之處,這才令庵野秀明可以大量借用宗教符號)。至於情節的部分,如果室友連第二次衝擊、第三次衝擊、使徒與 SEELE 等不同人物的目的是甚麼都不了解的話,我強烈建議有空可以看看 Eva Zone 這個網站。裡面有對情節極其詳盡的分析,看完絕對可以知道究竟整個故事在講甚麼。
注釋
嚴格而言,這裡說的是「我」存在,必然依賴於「非我」的存在。沒有「非我」便無所謂「我」。而「他者」一般指的是他人,他人只是眾多我以外的東西之中的一種。但「他者」的特性,在於他也是與我有同等地位的主體(下文會解釋這點),與其他能完全受我掌控的「物」不一樣。所以「他者」是「非我」中最為顯著者。
此處參考了沙特的《存在與虛無》與劇作《No Exit》。
此比喻啟發自朋友火鳳凰。
本文所談的主要是《新世紀福音戰士》的舊電視版 1-26 集,以及舊劇場版《The End of Evangelion》。漫畫版以及 2007 年開始上映的新劇場版不在討論範圍內。(編按:不過圖片有引用自劇場版的範圍。)
二千多年前,曾經有個叫蘇格拉底的人,因為荼毒青年而被判死,最終他把毒藥一飲而盡。好青年荼毒室中是一群對於哲學中毒已深的人,希望更多人開始領略、追問這世界的一切事物。在他們的帶領下,我們可能會發現我們習慣的一切不是這麼理所當然,從這一刻起接受好青年荼毒室 的哲學荼毒吧!
本文轉載自好青年荼毒室(哲學部) ,〈新世紀(EVA)的原罪、救贖與福音 〉。
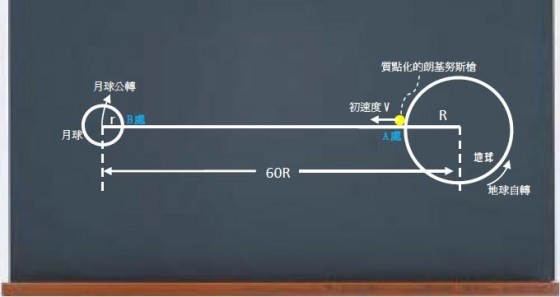
,故可得到第一個結論:當朗基努斯槍初速度 就可從地球表面飛到月球並插在月球表面上,也就可停留在繞月軌道上。
關係獲得。
。
,且 m= 80公噸,則
大約是將88163頭大象舉起的力量大小。
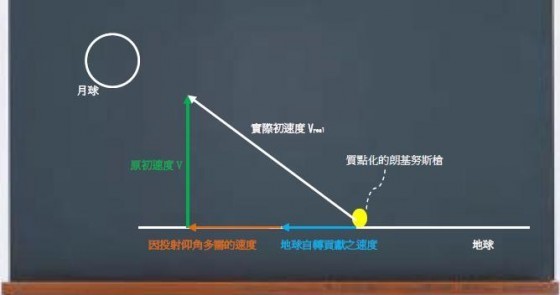
,而實際初動能為
,則
2. 空氣阻力造成的能量耗損