「數感盃青少年寫作競賽」提供國中、高中職學生在培養數學素養後,一個絕佳的發揮舞台。本競賽鼓勵學生跨領域學習,運用數學知識,培養及展現邏輯思考與文字撰寫的能力,盼提升臺灣青少年科普寫作的風氣以及對數學的興趣。
本文為 2018數感盃青少年寫作競賽 / 高中組專題報導類佳作 之作品,為盡量完整呈現學生之作品樣貌,本文除首圖及標點符號、錯字之外並未進行其他大幅度編修。

- 作者:楊子毅、吳冠宏/高雄市新莊高中
一、 研究緣起
「瀧、瀧」
聲音彷彿快要哭出來般急切,宛若遠處閃爍的星星般寂寞而顫抖。
──《你的名字》,小說,第 12 頁
從夢境中醒來,幽闃裡彷彿迴盪著一個孱弱的女聲,一次次呼喊著「瀧」,隨著簾後的暮光漸次逸散。今天下午第八次重看新海誠導演 2016 年所推出的動畫電影《你的名字》,簡直以為自己也和其中角色靈魂互換了……「黃昏之時啊,分身之時」。
難以忘懷那一幕:宮水三葉手持油性筆,正欲在立花瀧手心寫下名字時,夜晚降臨,「喀噠」一聲,筆掉落在地,三葉消失了;瀧腦海中關於三葉的記憶亦被不知名的力量一把抹去。 神秘的黃昏之時,在影片中不到短短的三分鐘,不禁令我們陷入長考:黃昏之時究竟有多長呢?能否以數學運算出其時間長短,讓相差三年時空的瀧和三葉,得以把握每一分秒,敘舊、 談心、想未來?如果可以再多個一分鐘,讓三葉寫完名字……
「……本來想告訴妳……」
「不論妳在世界上的哪一個角落,我一定會再去見妳。」
──《你的名字》,小說,第 202 頁
二、 文本回顧
於本章節,筆者先說明電影中的相關設定,諸如宮水一家的巫女體質、組扭編織、口嚼酒等,期以彰顯「黃昏之時」的重要性。
(一)宮水一家的巫女體質
在糸守小鎮的宮水一家,其巫女血統讓她們得以和另一個時空的人互換靈魂。此事來得突然,居住在東京的男高中生─瀧,一日驚醒,赫然發現自己變成名為三葉的女高中生!乍看又是一則時空穿越的窠臼,新海誠卻能賦予深意於這段奇異歷程:糸守小鎮即將被彗星摧毀,三葉和瀧必須及時通知居民避難,方能保全大家性命。
(二)組扭編織、口嚼酒
過去的一場大火導致古代文書付之一炬,故糸守的傳統文化組扭編織、口嚼酒等,均徒具形式,後人並不知悉其中真義。所謂「組扭編織」是把多種繽紛的細線纏繞成一條繩子, 完成後呈現各種圖案。而此條費時費工編織成的「組扭」,三葉先以其為髮帶,爾後轉贈瀧,瀧則將其綁於手腕作為幸運繩;此繩可謂兩人相遇相知的憑證與羈絆。外婆如此說道,把線連結在一起是「結」,把人連在一起也是「結」,時間的流動亦同,此為神明的名字和力量; 組扭編織亦是神明的技術,展現出時間的流動。此不僅深化組扭的意涵,亦優美詮釋出抽象的時間觀念。
而口嚼酒是三葉與瀧得以相見的關鍵之一。何也?外婆說道:「不論水、米或酒,只要是把食物放入身體的行為,也叫做『結』。因為進入身體的食物會和靈魂連在一起。」(p.88)瀧亦被告知此口嚼酒為三葉之「半身」,意即靈魂的一部份;因此,儘管三葉已死亡三年,當瀧飲下三葉的口嚼酒,即能與三葉再次進行暌違已久的靈魂互換。
(三)黃昏之時
文本中提及「黃昏之時」又稱「分身之時」,言簡意賅地埋下絕佳伏筆。日語中「彼何人(tasokare)」為「黃昏(tasogare)時分」的語源;由於傍晚非屬晝夜,兼以人的輪廓變得模糊、無從辨識,於此時可能遇到妖魔或死者,故亦可稱「逢魔時刻」。此外,文本中亦說明,於糸守小鎮,當提及「傍晚」,「分身之時」是最常聽聞的說法。由此可以推測,新海誠意圖結合「逢魔時刻」和「分身之時」二說,讓三葉與瀧終得相會於黃昏之時。
三、探究分析
根據民用黃昏的定義(註一),黃昏時間由太陽落到地平線以下(太陽仰角0°)開始計算,結束於太陽位在地平線下方 6°(即太陽仰角 -6°)。然而,當人們位於地球表面不同位置 時,太陽的仰角要如何計算呢?
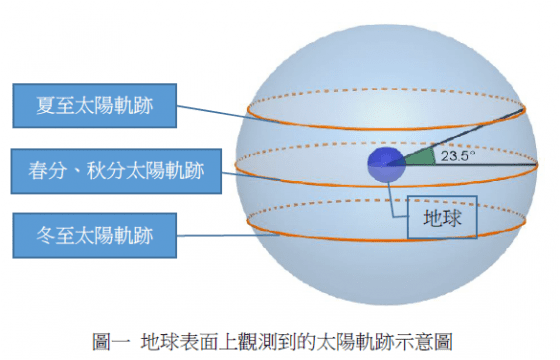
由於地球自轉之緣故,人在地球表面觀測太陽,可得太陽沿著赤道或緯圈面做相對運動, 亦即,假設以地球為中心(圖一中深藍小球),以人的視角看太陽每日的運動軌跡,可視為 太陽每日環繞地球一圈,以圖一中大球上的橘色圓圈為太陽某日期環繞地球的軌道,太陽在一年內的不同季節(日期)直射地球的不同緯度,最北為夏至時太陽直射北回歸線,最南則為冬至時直射南回歸線,如圖一。
假設太陽環繞地球的軌道為圓形(不考慮遠日點和近日點之影響),日地距離為 1AU, θ1為太陽一年內某日期直射之緯度(本文定義北緯緯度為正角,南緯緯度為負角),太陽軌道位於平面 z=sinθ1上,軌道半徑為 cosθ1,因此太陽軌道方程式為
\(\left\{\begin{matrix}
x^2+y^2=cos^2\theta_{1}\\z=sin\theta_{1}
\end{matrix}\right.\)
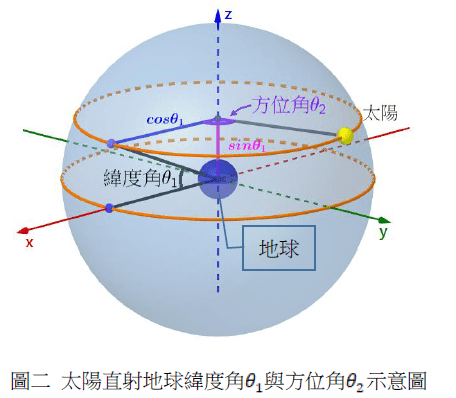
再假設單日內太陽與軌道圓心連線掃過的角度為太陽的方位角θ2(如圖二)
而方位角 360° 對應 24 小時,亦即方位角每轉動 15°,意味著時間經過一小時。由以下條件可得太陽的位置為
(cosθ1cosθ2,cosθ1sinθ2,sinθ1)
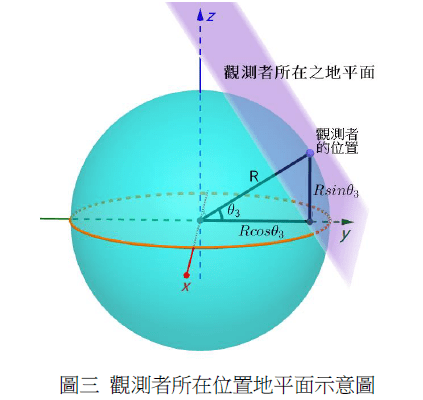
考慮觀測者所在之地平面,如圖三
假設觀測者所在緯度為θ3,無論觀測者所在之經度為何,其同日太陽軌道皆相同,為方便討論,不妨假設觀測者 x 座標為 0,則觀測者位置坐標為
(0,Rcosθ3,Rsinθ3)
因此地平面之法向量可為
(0,cosθ3,sinθ3)
而地平面方程式為
(cosθ3)y+(sinθ3)z = R(地球半徑)
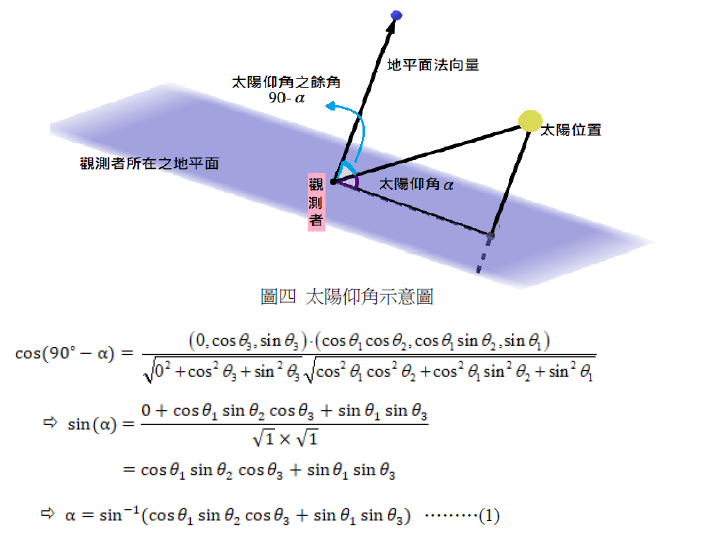
利用地平面法向量與太陽的位置向量求得太陽仰角之餘角(註二),即可得仰角,如圖四所示:
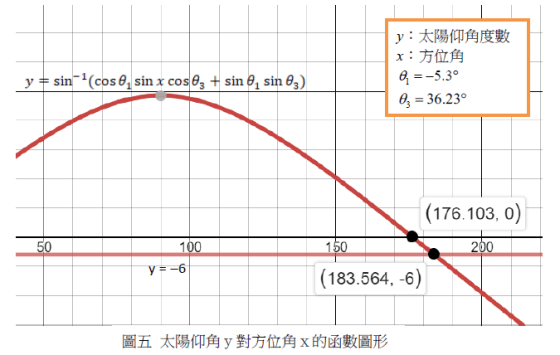
電影場景中,兩人見面日期為 10 月 4 日,當日太陽直射緯度 θ3= -5.3°,見面地點是日本岐阜縣飛驒市,所在緯度θ3,約為 36.23°,令方程式(1)中 α=y,θ2=x,繪製函數圖形如圖五
觀察太陽仰角與時間的關係,取出圖五中代表太陽仰角0°為的方位角θ2= 176.103,代表太陽仰角為-6° 的方位角θ2=183.564°,因此太陽在軌道平面上轉動方位角
(183.564-176.103)° = 7.461°
轉換成時間就是 \(7.461^{\circ}\times\frac{24 hr}{360^{\circ}}=0.479(hr)\doteqdot 29 (min)\)
在當日當時當地,黃昏之時只有短短的 29 分鐘,以致於三葉無法及時寫完名字,令人喟然,可不可以再延長一分鐘呢?
在文本中,三葉曾經抱怨糸守當地日照時間短,那麼,如果能移動到其他日照時間長之處,黃昏之時是否就能增加?運用相同方法計算同日期(10 月 4 日)各緯度黃昏時長,得表一如下。
觀察表一,我們發現日照短的高緯度地區,黃昏之時反而較久!為什麼呢?
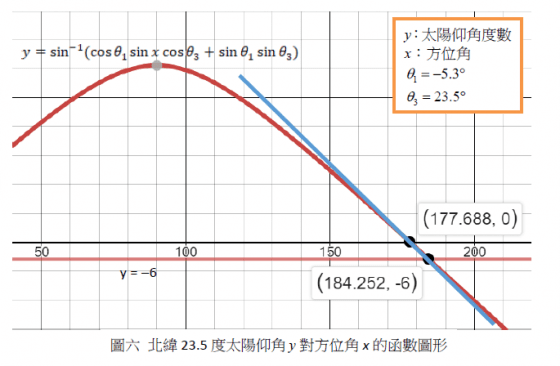
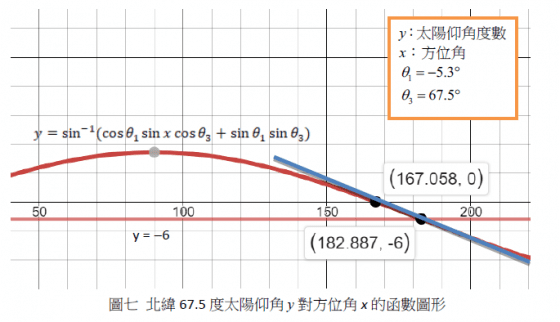
由圖六圖七可知,高緯度地區黃昏起迄點的割線斜率絕對值 |m|較低緯度小
\begin{equation}\left| m \right |=\left|\frac{y_2-y_1}{x_2-x_1} \right|=\left|\frac{**}{\Delta \theta_2} \right|\end{equation}
**為仰角變化量
由於仰角變化量相同,所以|m| 與方位角變化量 Δθ2 成反比,因高緯度之|m|較低緯度小,故高緯度的 Δθ2 較低緯度大,以致黃昏時距較長,所以瀧跟三葉如欲增加一分鐘的見面時間, 必須移至北緯 39 度之處(如岩手縣),然而兩地相距 268 公里,即使搭乘時速 200 公里的民用直升機也需費時 78 分鐘!真是令人遺憾,「多一分鐘」礙於現實而無法達成。
四、結論與建議
「黃昏之時」有 29 分鐘,應足夠讓兩人寫完名字;但接下來會出現一個問題:瀧寫的不是名字,而是「我喜歡妳」。那麼,即使黃昏之時再久,三葉依舊無法得知瀧的名字。為什麼瀧要這麼做呢?
這是因為,三葉不知道自己比瀧的時空早了三年,當她特地前往東京尋找瀧時,瀧冷淡的反應讓她心碎不已。爾後,瀧透過三葉的身體記憶,明白其心路歷程,因此他決定,這一次,換他不論天涯海角地尋覓三葉;就算她忘記他也無妨,只要她活下來、記得他的心意即可。所以,瀧想單方面獲得三葉的名字,這是一種守護的心情;其中關鍵,在於一定要算好 「黃昏之時」的長短,太早寫,情境不對味且有被發現之虞。對瀧而言,最完美的設想是,三葉寫完名字之後剛好消失;所以算出這 29 分鐘,著實意義非凡。瀧要拯救的不只是系守, 他真正最想做的是守護三葉,包含生命和心。
因此我們建議,瀧可以用前 26 分鐘,敘舊、談心、想未來,留 3 分鐘提議寫名字:1 分鐘偷寫告白,1 分鐘讓三葉寫名字,1 分鐘當作緩衝;如果沒事做,就執起三葉之手、淚眼相對(她不要偷看手心即可),以上。
———————————————————————————————————————-
註一 本文採用民用黃昏定義(civil twilight)
http://aa.usno.navy.mil/faq/docs/RST_defs.php
註二 由內積的定義,\(\vec{a}\cdot\vec{b}=\left|\vec{a}\right|\left|\vec{b}\right|\cos(X)\) (X為兩項量的夾角)
移項之後可得 \(\cos(X)=\frac{\vec{a}\cdot\vec{b}}{\left|\vec{a}\right|\left|\vec{b}\right|}\)