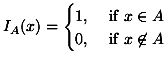公設化集合論的奧秘(18) 優雅的等式〡R〡=〡P(N)〡=〡2^N〡

延續之前的努力，我們雖然試過聯集（加法）和笛卡爾乘積（乘法），仍然沒能突破可數無限的藩籬，可見如來佛這隻手比我們想像中還要寬。在陷入困境的時刻，忽然想到在數學運算裡，減法和除法會讓數值變小，而加法和乘法會讓數值變大。但哪種運算可以讓數值增加得更「快」一些呢？ 我們任意拿兩個數，比如3和5來觀察看看：

3+5 = 8      3×5= 15    3⁵ = 243

我們發現對任意兩個正數，乘法得到的結果比加法得到的結果大，而指數運算得到的結果又比乘法大。依此進行推想，如果在集合運算裡有類似指數運算的話，那它很有可能就是我們得以突破可數無限集合的「星航艦企業號」，問題只剩下：這樣的東西存在嗎？

確實有這樣一個東西，它在日常數學（也就是非基礎數學）裡雖然並不常見，卻是集合論的「常備良藥」。我們就來見識一下它的模樣：

定義6：A和B都是集合，我們定義從A到B的所有函數所成的集合為B^A = {F〡F : A→ B為函數}

這個定義很容易讓人誤以為B^A指的就是函數 ƒ： A→ B，於是認為B^A只不過是函數ƒ 的另一個寫法罷了，但這種誤認卻是致命的。

當我們說函數 ƒ：A→B時，我們說的是某個特定的序對集合ƒ，這些序對的前項由A的元素構成而後項則由B的元素構成，所以函數ƒ的成員由序對形成。

舉個例子就能清楚了，比如A = 2而B = 3。那麼 ƒ 會是怎樣的型態呢？有人心裡可能會嘀咕說2和3不是自然數嗎？它們怎麼能夠充當定義域和對應域來形成函數呢？之所以有這種疑惑是因為集合論的馬步沒蹲扎實所致，才會忘了自然數本身就是集合啊！（請參考《公設化集合論的奧秘 (5)》） 所以自然數2 = {0, 1}，自然數3 = {0, 1, 2}，因此函數

ƒ: 2 → 3 就是
ƒ: {0, 1} → {0, 1, 2}。

現在我們可以據此定義一個個別函數，比如恆等函數（identity function） ƒ_i: x → x，它等於序對(0, 0) 和(1, 1) 所形成的集合{(0, 0), (1, 1)}。再比如說常數函數（constant function） ƒ_c: x → 2，則不論是0還是1，它們的函數值都等於2，所以函數ƒ_c就等於序對集合{(0, 2), (1, 2)}。

有了以上的例子我們澄清了B^A是從A到B的各種可能函數所形成的集合 {ƒ_i, ƒ_c, ƒ_s, …}，而不是任何特定函數ƒ_k。某個特定函數 ƒ: A→ B的成員是序對，但B^A的成員則是函數。接下來需要確認的是這個定義是否捕捉到指數的核心本質？我們可以問當A = 2且B = 3時，B^A有幾個成員？對於定義域的兩個元素0和1來說，它們各有3種選擇來形成序對，那就是（0, 0）、（0, 1）、（0, 2）和（1, 0）、（1, 1）、（1, 2）。

若要形成任何特定的函數ƒ_k，就必須從前面三個序對中選出某一個，然後再配上後面序對中的任一個，比如我們從前後都選第一個序對而形成{(0, 0), (1, 0)}這種函數組合。這樣的話所有可能的組合方式共有3+3+3 = 9種，也就是共有9個函數成員，正好是B^A=3² = 9。因此對於有限數值來說，B^A 的定義與指數運算相契合。

最後為了表明自己是公設化集合論的內行人，請不要忘記驗證B^A為「合法」集合。對於任意序對 (a, b)，a∈A且 b ∈ B 來說，( a, b) ∈ A X B，由於它們是函數的元素，所以由序對構成的函數F必定是A X B的子集，也就是F ⊆ A X B。由於冪集合是把子集作為元素而形成的集合，所以F ∈ P (A X B) 。我們在《公設化集合論的奧秘 (14)》中已經證明笛卡爾乘積A X B是集合，現在面對A X B 的冪集合P (A X B)，我們根據ZF7 冪集合公設得知P (A X B)也是集合，因此P (A X B)的子集B^A是集合沒錯。

有了B^A這個武器之後，我們發現可以將原先只限於有限數值的指數運算擴展到無限集合，比如說2^N。我們想知道這個運算是否能「飛出」可數無限集合的範圍? 對於有限數值的指數運算，我們有明確的規則和定義: 比如 2⁵ 就是將2連乘5次，而對任何自然數k，2^k就是將2連乘k次。在沒有定義B^A之前，我們並不知道2^N或2^ω代表甚麼意思，但我們現在知道2^N是指所有以下這種函數所成的集合:

F: {0, 1, 2, 3, 4…} → {0, 1}

這種集合的對應域很簡單，不過就是0跟1，那它看起來會像甚麼呢? 想像有一排被編上號碼的電燈泡，從最左邊的0號開始一直往右無盡延伸，越往右邊號碼越大，每個函數F就相當於一種亮燈的方式。比如若F定義域裡的所有自然數的値都對應到1，那就相當於燈泡全亮的狀態，反之如果F定義域裡的所有自然數値都對應到0，那就是燈泡全暗的狀態。依此類推，每個特定的F都表示一種亮燈狀態，而這些燈泡的各種明暗組合方式就構成2^N集合。

這看起來和我們在《公設化集合論的奧秘 (7)》裡提過的全體自然數的冪集合P(N)很像，所以我們要問: 2^N的尺寸是否與P(N)相同? 也就是它們的基數〡P(N)〡與〡2^N〡是否相等? 要證明這一點就必須在P(N)與2^N之間找到一個一對一且映成的函數ƒ，那樣就證明了〡P(N)〡=〡2^N〡。

由於P (N) 的元素是某個自然數的子集A ⊆ N，所以我們的目標是要將某個A（比如{0, 1, 2}）與2^N的元素之間建立起函數關係，也就是在

ƒ : P(N) → 2^N

之間尋找一對一且映成關係。但2^N的元素本身就是函數，該如何試當選取以完成這個艱難任務呢? 我們可以試著用特徵函數（characteristic function）來充當2^N的元素，其定義如下:

I_A: N → {0, 1}

它的意思是說如果某個x 剛好是A裡的元素，那麼它的函數值等於1，也就是這個編號的燈泡是亮的。反之若x不是A裡的元素，那函數值等於0，也就是這個編號的燈泡是暗的。因此我們可以把函數ƒ 看成是一張書面指令和燈泡明暗組合之間的對應關係，由P(N)裡挑選出來的子集A可以看成是一道指令，它裡面包含的元素就是要點亮的燈號。當這條指令經由ƒ 送到特徵函數I_A時，特徵函數就根據A指令佈署亮燈的方式，若函數值為1就是亮燈，若函數值為0就關燈。

我們以A = {0, 1, 2}作例子，A裡的元素等於是指令，讓我們依據指令將那幾個編號(0, 1, 2)的燈泡點亮，因此特徵函數據此進行判別之後就決定了一種亮燈的方式，也就是只有前3盞燈是亮的，而編號2之後的所有燈泡全是暗的。很容易可以看出若指令不同的話，也就是A ≠ B，則亮燈的方式也會有所不同，也就是I_A ≠ I_B。這就表示

ƒ : P(N) → 2^N
A → I_A

為一對一函數。反之對任何一種亮燈方式，也就是特徵函數IA，我們都可以找到某個指令A ∈ P(N) 使得ƒ (A) = I_A，因此ƒ為映成。既然ƒ 為一對一且映成函數，所以它們等量，也就是〡P(N)〡=〡2^N〡。

由於康托的對角線方法已經證明P(N)為不可數集合，因此與它等量的2^N也同樣為不可數集合。終於成功了！2^N運算讓我們擺脫可數無限的枷鎖而得以遨遊太虛之中，直達玄妙的不可數無限的領地，我們也使得冪集合P (N) 與2^N在此相遇。從無限尺寸的觀點來看，它們（P(N)和2^N）是同一個東西。在《公設化集合論的奧秘 (11)》裡我們證明了實數也是不可數的，那麼P(N)和2^N與實數的尺寸是否一樣大呢？有辦法可以證明嗎？這就只有等下回再分解了。

文 / 翁昌黎（《孔恩vs.波普》中文譯者）

許多人在學習集合論的過程中經常會聽到一個說法，那就是所有的集合都是從宇集（universe）—也就是所有集合所成的集合—裡拿出來的，彷彿先要有個上帝般的宇集，隨後所有的集合才從那裡生出。好比你要學習天文學，有人會告訴你我們住在一個大爆炸之後的廣大宇宙裡，然後依序介紹衛星、行星、恆星、太陽系、銀河系、星系團等等天文學「物件」。先給個最大的概念舞台，然後再進入舞台上的佈景和道具的細節，這樣的理解過程似乎合情合理。可是對集合論來說，這樣的說法是災難性的，不只是由於宇集的概念充滿詭異，而是宇集根本就不存在！

這到底是怎麼回事？才剛開始要碰觸現代數學核心的集合論概念，卻從一個完全錯誤的起點出發，這難道不讓人背脊發涼嗎？那就先來看看宇集到底長甚麼樣子吧！一般我們用大寫的V來代表宇集，所以根據素樸集合論的概括公設原理（請參考《公設化集合論的奧秘 (3)》），宇集就是：

V= {x〡x是個集合}   或者

V = {x〡x=x} （庫能等人使用這個寫法）

它們的意思很清楚，只要算是個集合都可以放進我們的大百寶箱V裡邊。但這樣做為什麼會有問題呢？既然要研究集合，那我們事先把所有的集合通通蒐羅起來形成一個最完整的集合有甚麼錯呢？

我們來觀察一下這個集合的形式有甚麼奇特之處，既然V是所有集合所成的集合，那V裡邊一定得有它自己，否則的話它就沒資格宣稱自己是包含所有集合的集合。因此V必然會有如下這種形態：

V= {a, b, c, d, e, … , V, x, y, z, …}

按照道理，宇集內部那個V（我們已經標成紅色）跟外面那個V是一樣的，因為宇集既然是宇宙間所有集合的集合，那它就是最大的集合，所以必然只有唯一的一個最大集合。因此：

V = {a, b, c, d, e, … , V, x, y, z, …}

把這個紅V套上去就應該是底下這種樣子：

V= {a, b, c, d, e, … , {a, b, c, d, e, … , V, x, y, z, …}, x, y, z, …}

而更裡面那個標紅的V也必定是複制了同樣的形態：

{a, b, c, d, e, … , V, x, y, z, …}

像這樣無窮無盡層層疊疊複制下去，永無盡頭。

頭被搞暈了吧？這樣的怪物到底是甚麼？雖說這樣的造形讓人頭暈目眩，但我們還是沒有充分的理由說它不存在。要如何證明它存在或不存在呢？如果你懷疑這樣的集合不存在該怎麼做呢？有一個很符合邏輯的想法就是，既然V「揚言」自己是所有集合所成的集合，那如果我們能夠製造出一個集合，然後證明它不在V裡，不就拆穿V的牛皮了嗎？但去哪裡找這個集合呢？

俗話說踏破鐵鞋無覓處，忽然想起一個老朋友R = { x 〡x ∉ x}，它不就是在《公設化集合論的奧秘 (3)》裡所談到的羅素詭論集合嗎？我們將其稍加改裝成為如下集合：

B = {x ∈ V 〡: x ∉ x}

這個微小的差異在於現在有個號稱包含一切集合的V，那麼任何集合都必須是它的成員才行，所以有x ∈ V這個條件。我們還可以接著問，B集合是它自己的成員嗎？如果是的話，那麼B ∈ B，則B必須符合上述集合的條件，也就是B ∈ V且B ∉ B

把它寫成數理邏輯式就是：

(L1)   B ∈ B ⇒ (B ∈ V) · (B ∉ B)    （其中黑點為and的意思）

反過來說，如果B ∉ B，那麼根據假設，V包含一切集合，所以B ∈ V，這樣的話B剛好又符合集合B = {x ∈ V 〡: x ∉ x}的條件，所B ∈ B。

整理成理邏輯式就成了：

(L2)    (B ∈ V) · (B ∉ B) ⇒ B ∈ B

把(L1)和(L2)組合起來可以得到一個雙條件句:

(L3)     B ∈ B ⇔ (B ∈ V) · (B ∉ B) 

學過一點數理邏輯的人都知道，符號⇔兩邊的邏輯語句等值，也就是兩邊必須同為真或同為假整個邏輯式才能成立。但由於B ∉ B是B ∈ B的否定，所以它們必定一真一假，那麼邏輯式 (L3) 為真的唯一希望就是B ∈ V為假了。因為若B ∈ V為真，那兩邊的另兩個語句永遠一真一假，(L3) 就永遠沒有成真的希望了。因此根據邏輯，我們得出B ∈ V為假，也就是B ∉ V。

這個結論的重要性在於既然有一個集合B不在V裡，那表示V根本不是包含一切集合的集合，牛皮終於吹爆，詐騙案宣告偵破。換句話說，那樣的集合V並不存在。

因此宇集V和羅素集合R一樣，都會導致邏輯矛盾，因此都成為公設化集合論「掃黑」的對象。在集合論發展的過程裡，對於排除這種搗蛋分子有兩條路線，一個是我們一開始採用的ZF集合論，它直接將這種龐然怪物趕出集合的園子，塑造了一個純淨的理念世界，其中只有一種物件（集合）和一種關係（∈），不需要其他多餘的材料。

ZF系統如何處理羅素詭論我們已經在《公設化集合論的奧秘(4)》裡談過了，現在簡短介紹一下另一條路線的主要系統NBG如何面對這種邏輯困境。所謂NBG是這個系統的三個主要貢獻者的名字縮寫，這個陣容也是夠嚇人的。N是被稱為神童的電腦之父馮·紐曼（John von Neumann），B是瑞士知名數學家伯納斯（Paul Bernays），證明論的現代奠基者根岑（Gerhard Gentzen）就是他的弟子，G不用說就是大名鼎鼎的哥德爾。

NBG系統的最大特徵是它用類（class）來函蓋所談論的理論對象，集合是類的一種，而那些不屬於集合的V和R則稱為真類（proper class），但在ZF系統裡是不談論真類的，所以在進入NBG系統之前必須先定義好集合和真類以免混淆。一般用M(X)來代表X是個集合，用邏輯表達式(∃Y)( X∈Y)來定義。它的意思是說如果X是集合，那它可以被登記在另一個集合之下成為它的成員。但真類無法這樣，所以它的定義就是M(X)的否定(寫成¬M(X))，因為它們無法被登記在任何集合之下成為成員，所以真類不是集合。或者換個說法，如果一個類可以登記在其他集合名下，那這個類就稱為集合，如果不可以登記在任何集合名下就稱之為真類。

按照這個新規定，我們發現之前為宇集V所做的造型

V= {a, b, c, d, e, … , V, x, y, z, …}就不能存在了。

首先紅V沒有資格登記在任何集合名下，況且外邊那個V（當然是同一個V）也不是集合，兩個集合的條件都不符合，在這種裡外不是人的情況下，我們之前對宇集那令人頭昏腦脹的構造方式瞬間煙消雲散，好似鬼魅夜間幻化的亭台樓閣到了白晝只剩下荒草間的荒塚。

雖然NBG理論系統可以合法談論真類，算是一種擴張了的類理論而不僅是集合論，但從集合和真類的定義（也就是M(X)和¬M(X)）可以知道，類並不是集合。所以在集合論的領域裡，兩者並無本質差異，也就是NBG並沒有因為加入真類而推導出某些ZF所沒有的定理。

由於真類會在集合系統裡引發邏輯矛盾，所以NBG將其納入並非改變或擴展集合的定義，只是一種權宜之計。它認為在探討一個理論時，若給「非集合」一個代表符號則能增加理論符號系統的表達力，對理論探索來說不見得是壞事。正如聊齋裡談到很多鬼靈精怪的故事，它給我們增加了許多生活的樂趣，但不表示這些名稱所說的東西就真的存在。

僅管NBG有那麼強的卡司陣容和理論表達力，但在集合論領域的普及程度卻趕不上ZF，其中一個原因還是在於理論的簡潔和美感。ZF集合論讓你看到一個純淨而單一的世界，裡面沒有塵土只有琉璃和寶石，沒有魑魅魍魎只有潔白的柏拉圖地磚。

文 / 翁昌黎（《孔恩vs.波普》中文譯者）

想像你在一個一望無際的沙灘，晶瑩的海岸由近乎純白質地的細沙構成，在陽光下閃爍著寶石般的光輝。天空有一條發出橙色亮光的細線，似有似無，那是柏拉圖世界裡的實數線投影到這個神奇星球的擬似影像。

假設每顆沙粒代表一個集合，將這些沙粒灑向這條實數線企圖將它填滿，你會發現這些純白的細沙集合像是消失了一般，完全不影響橙色實數線的顏色，因為沙粒實在太稀少了。

就算你得到一種魔法，能在瞬間將這些無窮沙粒悉數灑在數線上，可是實數線上依然觀察不到白沙的蹤跡，因為它們仍然太過稀少。我們再度向孫悟空的師父菩提祖師求救，請他老人家傳授一個厲害點的法術，可以將剛剛灑出去的每一粒沙都變成等同於這個無窮沙灘世界的所有沙粒。但你將失望地發現，雖然親眼見識了菩提祖師將一沙粒化成無窮沙數世界的絕活，可是實數線上卻依然沒有任何一點斑白的痕跡，就好像這些從無數再化成無數的沙粒憑空消失一樣。

這到底是怎麼回事？理由是它們仍然太過稀少，所以無法蓋住實數線，甚至無法顯示出它們的存在。如果我們能夠把無窮顆沙粒集合和實數線投射到我們這個時空，那你所看到的場景大概就會有如以上的描述，可數無限顆沙粒再變現出可數無限顆沙粒的總合對於實數線來說依然是杯水車薪。

為了證明整個實數集合確實比可數無限集合還大，我們先來觀察一個現象：把（–1, 1）這個實數開區間彎成半圓形，如下圖藍線部分所示。假設藍線左邊的端點是–1，而右邊的端點是1，垂直的紅虛線劃過的點是原點 0，所以垂直紅虛線的左半邊正好是負實數而右半邊則是正實數。

從虛擬的圓心處往黑色實數線用紅色虛線連接，你會發現每一個區間（–1, 1）內的數都正好對應到黑線上的另一個實數。而當虛線接近水平線時，左右兩邊對應到黑色數線的絕對值就會變很大，且所對應的實數越來越趨近於（–∞, ∞）。因此（–1, 1）區間內的實數和（–∞, ∞）區間內的實數（等於是R）有一對一且映成的關係。那麼根據定義，（–1, 1）區間裡的實數與全體實數R等量。

假設區間（–1, 1）中所有實數的集合為I，則基數〡I〡=〡R〡，也就是說區間（–1, 1）裡的實數個數與所有實數集合的個數一樣多。以上這個方法稱之為幾何學證明。雖然直觀上沒有問題，但站在集合論的立場，我們應該要想有沒有更嚴格的數學證明呢？這下可傷腦筋了，根據我們目前的數學知識配備，若要證明〡I〡=〡R〡，則需要找到一個從I到R的一對一且映成的函數才行。那麼到哪裡去找這麼個函數呢？

正所謂眾裡尋它千百度，驀然回首那傢伙就在正切函數（tan）處。我們發現當tan的x值趨近於–π/2時，它的y值會向–∞逼近，而當tan 的x值趨近π/2時，它的y值會向∞逼近，而且任何一個x值只對應到一個y值。這不就是說正切函數tan在（–π/2, π/2）與全體實數R之間形成一對一且映成？tan：（–π/2, π/2）→（–∞, ∞）不就是夢寐以求的答案？

但剛剛的幾何證明說的是（–1, 1）→（–∞, ∞）有一對一且映成函數而不是（–π/2, π/2）→（–∞, ∞），眼看就要得手了卻差一步，該怎麼辦呢？只要設法把（–π/2, π/2）變成（–1, 1）不就好了？但我們的野心還要大一些，我們希望把（–π/2, π/2）→（–∞, ∞）的函數變成（0, 1）→（–∞, ∞）的函數，理由待會兒馬上會揭曉。

這個函數首先要把（0, 1）區間裡的每個x轉變成（–π/2, π/2）區間裡的某個y，但因為tan(y)就會把每個y從（–π/2, π/2）映射到（–∞, ∞），因此我們要找的函數就是某個用x來表達的正切函數，我們發現經由線性變換可以找到這個函數。既然我們想把某個（0, 1）區間裡的x變成（–π/2, π/2）區間裡的某個y，於是問題相當於把某個（0, 1）區間裡的x轉換成π/2 (–1, 1)區間裡的某個y，它們的關係式是：

π/2 (a x +b) =y

我們先把π/2提出來，待會兒再放回去，計算上會方便很多，因此：

當x = 0的時候 y= –1，代入式子得到b= –1

當x = 1的時候 y= 1，代入式子得到a= 2

把a和b的值放回關係式得到π/2 (2 x–1) =y 。

就是它了：函數 tan[π/2 (2 x–1)] 可以把（0, 1）區間裡的實數一一對映到所有實數，因此我們用數學分析的方法證明了（0, 1）區間裡的實數和整個實數一樣多，比剛剛的幾何證明方法又進了一步。

這個結果夠驚人的了，這麼小段的（0, 1）區間裡的實數居然和整個R一樣多，但我們更想進一步知道R是否也是可數無限？對於這個問題康托總共給出兩個完全不同證明方法，第一個是在1874年提出的，其中用到集合的排序和有界（bounded）的概念。第二個證明直到1891年才提出，採用的正是康托拿手的對角線證明法，我們就再次來看看康托如何拿這項精妙的數學武器來對付巨大的實數尺吋。

因為剛剛已經證明了R和區間（0, 1）等量，所以只要證明（0, 1）區間裡的實數是否可數就等於證明了R是否可數， 這大大簡化了我們的工作，剛剛些許辛苦還是值得的。由於這個區間內的實數都能用無限小數的展開形式來表示，假設它們的個數是可數的話，那我們就能將區間裡的實數編上序號，比如：

r₁ = 0.320059874…

r₂ = 0.912533121…

r₃ = 0.007213568…

r₄ = 0.552418792…

r₅ = 0.778451420…

r₆ = 0.118841234…

r₇ = 0.665590012…

…

…

需要注意的是，由於0.99999…等於1，所以在這個可數無限序列裡0.999999…的寫法被排除掉。

現在我們用一種特別的方法來製造一個新的實數x，那就是對任何小數點之後的數進行改裝，凡是遇到1就把它改成2，凡是遇到1以外的數（比如0, 2, 3, 4, 5, 6,  …）就把它改成1。我們拿以上的實數序列作例子，依次取小數點後面的第1, 2, 3, 4, 5, 6, …位，也就是按照對角線的方向來進行改造。

我們看到r₁小數點後的第1個位數是3（如紅色數字所示），所以依照規定將其改成1，r₂小數點後的第2個位數是1 ，所以依照規定改成2。依此類推，我們得到一個新的實數

x = 0.1211121…

這個數字的特點是它不同於r₁，因為小數點後第1位數不相等，它也不等於r₂，因為小數點後第2位數不相等。依此類推，我們依照此法製造出來的數字x不等於任何序列中的數字。但它明明是（0, 1）區間裡的實數，所以與一開始的假設相矛盾。我們得到（0, 1）區間裡的實數是不可數這個結論，因此，實數R也是不可數的。

原來，R的個數比可數的N和Q都要來得大。於是一個疑問自然浮現：在《公設化集合論的奧秘 (7)》一文裡，我們也是用對角線法證明了全體自然數N的冪集合P(N) 的元素個數同樣是不可數，那麼自然數冪集合的基數〡P(N)〡是否等於實數的基數〡R〡呢？ 這兩種不可數集合其尺寸會一樣大嗎？我們又如何知道它們是否有相同的尺寸呢？這些問題只有等下回再分解囉！

有一種說法認為集合論的發明是在1873年12月，精確地說是1873年12月7日，因為那一天康托證明了連續統（continuum）是不可數的，所以應該把那一天當成現代集合論的生日。不論你是否同意這個出生證明，但康托1873年年底所用的證明方法並非後來廣為人知的對角線法，也就是我們在《公設化集合論的奧秘 (11)》所採用的方法，對角線法的提出要到大約19年後的1892年才公諸於眾。

但從那一天起，人類對無限的了解進入了一個全新的階段，我們知道實數（連續統）比自然數還大。在證明實數是不可數之後，我們可否進一步下結論說自然數的冪集合P(N)與實數的尺寸一樣大，因為它們都是不可數集合？在沒發現不可數集合之前，我們原以為無限只有一種，那就是像自然數一樣可以從0, 1, 2, 3, 4, 5, 6 … 一直往下數沒有盡頭這種無限，直到這種想法被康托的證明方法擊碎。有了這個教訓，我們最好更加謹慎，任何直觀的想法都應該由嚴格的證明來確認，所以尋找證明是必要的工作。

假如要證明實數集合R與P(N) 等量，那麼根據定義1 （請參考《公設化集合論的奧秘 (8)》） ，就必須找到一個一對一且映成的函數F: R → P(N)才行。但這可不是件容易的事，我們如何在浩如星辰的實數和全體自然數的冪集合之間找到這種一一對應呢？先別失望，我們之前介紹的戴德金左集合（請參考《公設化集合論的奧秘 (16)》和《公設化集合論的奧秘 (17)》）或許可以在此危難之際發揮作用。由於戴德金實數是由一堆有理數（實際上是可數無限個）來定義的，這給了我們一個透視實數集合結構的絕佳機會。

既然每個戴德金實數就相當於無限多個有理數的集合，比如0被定義為 {q〡q ∈ Q 且q<0}，也就是所有負有理數的集合，那我們正好可以定義一個一對一的恆等函數，使得每個實數r （相當於一個戴德金左集合）對應到一個相等的有理數子集合：

f: R → P(Q)

 r → r

也就是說定義域R裡裝了哪一堆有理數那我的値域就取同樣一堆有理數來配對，因為這樣一堆有理數正好符合對應域P(Q)的定義條件—全體有理數的子集合。這麼容易就完成證明啦？還是個恆等函數，這也簡單到有點欺負人了吧！

且慢，有兩個問題尚待解決。首先，我們所要證明的函數關係是從 R → P(N)而不是R → P(Q)。其次，R和P(N)等量的條件是找到一個一對一且映成的函數，但我們剛剛找的f: R → P(Q)只滿足一對一的條件卻不映成，這一點可以很容易看出來。由於戴德金實數必定由無限個有理數所構成，因為左集合會往負數方向無限伸展，可是對於P(Q)來說，它顯然也必須包含由有限元素所構成的集合，比如{1/6, 37, 522}就是Q的一個有限子集合，但我們無法找到與之相對應的戴德金實數r。

現在回顧《公設化集合論的奧秘 (14)》裡的定義：

定義5：如果在集合A和B之間存在一個一對一函數ƒ : A→B，則說A小於或等量於B，寫成A ≤ B。相當於〡A〡≤  〡B〡，也就是A的基數小於等於B的基數。

由這個定義得知，我們目前能確定的只是〡R〡≤ 〡P(Q)〡，而不是〡R〡= 〡P(N)〡。證明定理有時候就像擬訂作戰策略，對於無法一次消滅的敵人，你要分段把它逐步吃掉，而不能急於蟒蛇吞象最後把自己噎死。千萬不要輕忽每一次的小進展，那就讓我們把以上成果當成是一個好的開始吧。

有了半壁江山，就想辦法湊出另一半吧！這提醒我們之前提到的施洛德—伯恩斯坦定理（Schröder-Bernstein theorem） ，它的一般表述形式是：

對任意集合A和B，如果〡A〡≤ 〡B〡且〡B〡≤ 〡A〡

則〡A〡=〡B〡。

這個定理的威力在於它允許我們使用和有限數值一樣的方式來辨認集合的尺寸。比如有兩個數a和 b，如果a ≤ b 而且b ≤ a的話，那一定會得出a = b，施洛德—伯恩斯坦定理把這層關係從有限數推廣到不可數無限集合。

此外，這個定理還有一個實際功能，那就是當我們想證明兩個集合等量卻苦於找不到一對一且映成函數時，可以有個更簡潔的辦法。我們只需找到兩個一對一函數，一個從A到B，另一個從B到A就成了，對於許多複雜的集合等量證明來說，這不啻是天降福音。接下來只須稍稍解決一個小問題，那就是之前我們已經證明有理數和自然數一樣多（《公設化集合論的奧秘 (9)》），所以〡Q〡=〡N〡，得到〡P(Q)〡=〡P(N)〡，因此原來的戰鬥成果〡R〡≤ 〡P(Q)〡就可以順理成章地變成〡R〡≤ 〡P(Q)〡=〡P(N)〡，用小學的數學就能得到〡R〡≤ 〡P(N)〡。

以施洛德—伯恩斯坦定理的觀點來看，證明已經完成了一半。接下來我們想要在2^N和R之間建立起一個一對一函數，也就是讓〡2^N 〡≤ 〡R〡成立。我們再次用小學數學來解釋這樣做的理由，在《公設化集合論的奧秘 (15)》我們證明了〡P(N)〡=〡2^N〡，因此只要〡2^N 〡≤ 〡R〡成立，那麼〡P(N)〡≤ 〡R〡就會成立。

這讓我想起一個卡通節目，每次當兩位總在冒險旅途的主角一遇到甚麼災難，只要把兩枚原本一體的神奇戒指結合，就會跑出一個法力無邊的阿拉伯神祇名叫蘇仙，祂的神通可以打退各方的妖魔鬼怪。數學式〡R〡≤ 〡P(N)〡和〡P(N)〡≤ 〡R〡就有如集合論中的神奇戒指，當它們一結合就能招喚出法力無窮的蘇仙讓我們見識到集合論的奇蹟：〡R〡= 〡P(N)〡。

但要如何打造另外一半的戒指呢？我們需要找到一個一對一函數

θ: 2^N → R

之前說過2^N是指以下這種函數類型所成的集合

F: {0, 1, 2, 3, 4…} → {0, 1}

所以我們的目標是找一個這種類型的函數f對應到某個實數r。它的形式就是：

θ: 2^N → R

     f →  r

化繁為簡是數學思考的靈魂，所以在尋找f之前我們先將θ的對應域R做點簡化工作。在《公設化集合論的奧秘 (11)》一文我們已經證明全體實數R的個數和開區間(0, 1)裡的實數一樣多，因此我們可以把目標函數θ: 2^N → R調整為θ: 2^N → (0, 1)，也就是讓2^N 中的元素f對應到(0, 1)間的某個實數即可。這個函數的樣貌如下：

θ: 2^N →(0, 1)

     f →  0.a₀a₁a₂a₃a₄…a_n…

我們之前介紹過 2^N的成員，它的成員是某個函數f，有如一排編上號碼從0一直延伸至無窮的燈泡，每個燈泡可以是亮燈或關閉的狀態，而f就相當於某種特定的亮燈組合方式。比如現在給出一種亮燈組合，它規定只有第一個編號為0的燈點亮，其餘所有的燈都是暗的，這時f函數的値有如下的規律：

f(0) = 1, f(1) = 0, f(2) = 0, f(3) = 0, f(4) = 0,  … f(n) = 0 …

每個不同的函數f代表一種特定的亮燈組合方式。

現在只要把f的第一個函數值f(0)指定為a₀ ，第二個函數值f(1)指定為a₁，第三個值f(2)指定為a₂，依此類推，我們就能夠得到一個介於0和1之間的實數，其小數點之後的位數只由0與1構成。以剛才的函數為例，我們得到a₀ =1, a₁=0, a₂=0, a₃=0… 因此和它對應的實數就是0.100000000…，也就是0.1。顯然如果函數不同f₁ ≠ f₂，則其指定的每個a_n值當然不同，這就導致與其相對應的實數0.a₀a₁a₂a₃a₄…a_n …也不同，於是我們得到 θ(f₁) ≠ θ(f₂)，因此θ為一對一函數。於是我們證明了蘇仙戒指的另一半：

〡2^N 〡= 〡P(N)〡≤ 〡R〡

於是我們所知道的不可數集合的三種形態全部等量，形成一個相當優雅簡潔的集合等式〡R〡= 〡P(N)〡=〡2^N〡。

我們之前用ℵ₀來標示自然數和有理數這種可數無限集合的基數，因此我們有等式：

〡N〡= 〡Q〡= ℵ₀

而對於比ℵ₀還大的不可數集合我們用ℵ₁來表示，因此又有如下的等式：

〡R〡= 〡P(N)〡=〡2^N〡= ℵ₁

經過長期的努力，我們終於將這些主要的無限集合之間的尺寸關係弄清楚了， 但這就是故事的終點了嗎？發揮想像力，朝著變大和變小的方向飛行，兩個有趣的問題又會浮現出來。第一個問題是有比ℵ₁更大的集合嗎？如果有，那要如何才能發現它呢？或者怎樣才能把它製造出來呢？第二個問題是在ℵ₀和ℵ₁之間有沒有一種中等尺寸的無限集合，它既比ℵ₀大但又比ℵ₁小，比如說是否存在一個基數為ℵ_1/2的集合？要回答這些有趣的問題就只有等下回再分解了！