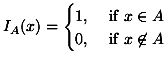公設化集合論的奧秘(15) 突破可數無限的星航艦企業號

credit ： CC by Tim Sackton @ flickr

延續之前的努力，我們雖然試過聯集（加法）和笛卡爾乘積（乘法），仍然沒能突破可數無限的藩籬，可見如來佛這隻手比我們想像中還要寬。在陷入困境的時刻，忽然想到在數學運算裡，減法和除法會讓數值變小，而加法和乘法會讓數值變大。但哪種運算可以讓數值增加得更「快」一些呢？ 我們任意拿兩個數，比如3和5來觀察看看：

3+5 = 8      3×5= 15    3⁵ = 243

我們發現對任意兩個正數，乘法得到的結果比加法得到的結果大，而指數運算得到的結果又比乘法大。依此進行推想，如果在集合運算裡有類似指數運算的話，那它很有可能就是我們得以突破可數無限集合的「星航艦企業號」，問題只剩下：這樣的東西存在嗎？

確實有這樣一個東西，它在日常數學（也就是非基礎數學）裡雖然並不常見，卻是集合論的「常備良藥」。我們就來見識一下它的模樣：

定義6：A和B都是集合，我們定義從A到B的所有函數所成的集合為B^A = {F〡F : A→ B為函數}

這個定義很容易讓人誤以為B^A指的就是函數 ƒ： A→ B，於是認為B^A只不過是函數ƒ 的另一個寫法罷了，但這種誤認卻是致命的。

當我們說函數 ƒ：A→B時，我們說的是某個特定的序對集合ƒ，這些序對的前項由A的元素構成而後項則由B的元素構成，所以函數ƒ的成員由序對形成。

舉個例子就能清楚了，比如A = 2而B = 3。那麼 ƒ 會是怎樣的型態呢？有人心裡可能會嘀咕說2和3不是自然數嗎？它們怎麼能夠充當定義域和對應域來形成函數呢？之所以有這種疑惑是因為集合論的馬步沒蹲扎實所致，才會忘了自然數本身就是集合啊！（請參考《公設化集合論的奧秘 (5)》） 所以自然數2 = {0, 1}，自然數3 = {0, 1, 2}，因此函數

ƒ: 2 → 3 就是
ƒ: {0, 1} → {0, 1, 2}。

現在我們可以據此定義一個個別函數，比如恆等函數（identity function） ƒ_i: x → x，它等於序對(0, 0) 和(1, 1) 所形成的集合{(0, 0), (1, 1)}。再比如說常數函數（constant function） ƒ_c: x → 2，則不論是0還是1，它們的函數值都等於2，所以函數ƒ_c就等於序對集合{(0, 2), (1, 2)}。

有了以上的例子我們澄清了B^A是從A到B的各種可能函數所形成的集合 {ƒ_i, ƒ_c, ƒ_s, …}，而不是任何特定函數ƒ_k。某個特定函數 ƒ: A→ B的成員是序對，但B^A的成員則是函數。接下來需要確認的是這個定義是否捕捉到指數的核心本質？我們可以問當A = 2且B = 3時，B^A有幾個成員？對於定義域的兩個元素0和1來說，它們各有3種選擇來形成序對，那就是（0, 0）、（0, 1）、（0, 2）和（1, 0）、（1, 1）、（1, 2）。

若要形成任何特定的函數ƒ_k，就必須從前面三個序對中選出某一個，然後再配上後面序對中的任一個，比如我們從前後都選第一個序對而形成{(0, 0), (1, 0)}這種函數組合。這樣的話所有可能的組合方式共有3+3+3 = 9種，也就是共有9個函數成員，正好是B^A=3² = 9。因此對於有限數值來說，B^A 的定義與指數運算相契合。

最後為了表明自己是公設化集合論的內行人，請不要忘記驗證B^A為「合法」集合。對於任意序對 (a, b)，a∈A且 b ∈ B 來說，( a, b) ∈ A X B，由於它們是函數的元素，所以由序對構成的函數F必定是A X B的子集，也就是F ⊆ A X B。由於冪集合是把子集作為元素而形成的集合，所以F ∈ P (A X B) 。我們在《公設化集合論的奧秘 (14)》中已經證明笛卡爾乘積A X B是集合，現在面對A X B 的冪集合P (A X B)，我們根據ZF7 冪集合公設得知P (A X B)也是集合，因此P (A X B)的子集B^A是集合沒錯。

有了B^A這個武器之後，我們發現可以將原先只限於有限數值的指數運算擴展到無限集合，比如說2^N。我們想知道這個運算是否能「飛出」可數無限集合的範圍? 對於有限數值的指數運算，我們有明確的規則和定義: 比如 2⁵ 就是將2連乘5次，而對任何自然數k，2^k就是將2連乘k次。在沒有定義B^A之前，我們並不知道2^N或2^ω代表甚麼意思，但我們現在知道2^N是指所有以下這種函數所成的集合:

F: {0, 1, 2, 3, 4…} → {0, 1}

這種集合的對應域很簡單，不過就是0跟1，那它看起來會像甚麼呢? 想像有一排被編上號碼的電燈泡，從最左邊的0號開始一直往右無盡延伸，越往右邊號碼越大，每個函數F就相當於一種亮燈的方式。比如若F定義域裡的所有自然數的値都對應到1，那就相當於燈泡全亮的狀態，反之如果F定義域裡的所有自然數値都對應到0，那就是燈泡全暗的狀態。依此類推，每個特定的F都表示一種亮燈狀態，而這些燈泡的各種明暗組合方式就構成2^N集合。

這看起來和我們在《公設化集合論的奧秘 (7)》裡提過的全體自然數的冪集合P(N)很像，所以我們要問: 2^N的尺寸是否與P(N)相同? 也就是它們的基數〡P(N)〡與〡2^N〡是否相等? 要證明這一點就必須在P(N)與2^N之間找到一個一對一且映成的函數ƒ，那樣就證明了〡P(N)〡=〡2^N〡。

由於P (N) 的元素是某個自然數的子集A ⊆ N，所以我們的目標是要將某個A（比如{0, 1, 2}）與2^N的元素之間建立起函數關係，也就是在

ƒ : P(N) → 2^N

之間尋找一對一且映成關係。但2^N的元素本身就是函數，該如何試當選取以完成這個艱難任務呢? 我們可以試著用特徵函數（characteristic function）來充當2^N的元素，其定義如下:

I_A: N → {0, 1}

它的意思是說如果某個x 剛好是A裡的元素，那麼它的函數值等於1，也就是這個編號的燈泡是亮的。反之若x不是A裡的元素，那函數值等於0，也就是這個編號的燈泡是暗的。因此我們可以把函數ƒ 看成是一張書面指令和燈泡明暗組合之間的對應關係，由P(N)裡挑選出來的子集A可以看成是一道指令，它裡面包含的元素就是要點亮的燈號。當這條指令經由ƒ 送到特徵函數I_A時，特徵函數就根據A指令佈署亮燈的方式，若函數值為1就是亮燈，若函數值為0就關燈。

我們以A = {0, 1, 2}作例子，A裡的元素等於是指令，讓我們依據指令將那幾個編號(0, 1, 2)的燈泡點亮，因此特徵函數據此進行判別之後就決定了一種亮燈的方式，也就是只有前3盞燈是亮的，而編號2之後的所有燈泡全是暗的。很容易可以看出若指令不同的話，也就是A ≠ B，則亮燈的方式也會有所不同，也就是I_A ≠ I_B。這就表示

ƒ : P(N) → 2^N
A → I_A

為一對一函數。反之對任何一種亮燈方式，也就是特徵函數IA，我們都可以找到某個指令A ∈ P(N) 使得ƒ (A) = I_A，因此ƒ為映成。既然ƒ 為一對一且映成函數，所以它們等量，也就是〡P(N)〡=〡2^N〡。

由於康托的對角線方法已經證明P(N)為不可數集合，因此與它等量的2^N也同樣為不可數集合。終於成功了！2^N運算讓我們擺脫可數無限的枷鎖而得以遨遊太虛之中，直達玄妙的不可數無限的領地，我們也使得冪集合P (N) 與2^N在此相遇。從無限尺寸的觀點來看，它們（P(N)和2^N）是同一個東西。在《公設化集合論的奧秘 (11)》裡我們證明了實數也是不可數的，那麼P(N)和2^N與實數的尺寸是否一樣大呢？有辦法可以證明嗎？這就只有等下回再分解了。

泛科學總編輯鄭國威招牌課程再度開課，面對面傳授閱讀理解、科普寫作到內容行銷的心法，幫助你打造個人品牌。

慶祝泛科學院周年慶，快來領取專屬優惠，現在購買課程還有機會抽中 $1,111 折價券喔！課程傳送門請點我