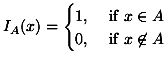文 / 翁昌黎(《孔恩vs.波普》中文譯者)
許多人在學習集合論的過程中經常會聽到一個說法,那就是所有的集合都是從宇集(universe)—也就是所有集合所成的集合—裡拿出來的,彷彿先要有個上帝般的宇集,隨後所有的集合才從那裡生出。好比你要學習天文學,有人會告訴你我們住在一個大爆炸之後的廣大宇宙裡,然後依序介紹衛星、行星、恆星、太陽系、銀河系、星系團等等天文學「物件」。先給個最大的概念舞台,然後再進入舞台上的佈景和道具的細節,這樣的理解過程似乎合情合理。可是對集合論來說,這樣的說法是災難性的,不只是由於宇集的概念充滿詭異,而是宇集根本就不存在!
這到底是怎麼回事?才剛開始要碰觸現代數學核心的集合論概念,卻從一個完全錯誤的起點出發,這難道不讓人背脊發涼嗎?那就先來看看宇集到底長甚麼樣子吧!一般我們用大寫的V來代表宇集,所以根據素樸集合論的概括公設原理(請參考《公設化集合論的奧秘 (3)》),宇集就是:
V= {x〡x是個集合} 或者
V = {x〡x=x} (庫能等人使用這個寫法)
它們的意思很清楚,只要算是個集合都可以放進我們的大百寶箱V裡邊。但這樣做為什麼會有問題呢?既然要研究集合,那我們事先把所有的集合通通蒐羅起來形成一個最完整的集合有甚麼錯呢?
我們來觀察一下這個集合的形式有甚麼奇特之處,既然V是所有集合所成的集合,那V裡邊一定得有它自己,否則的話它就沒資格宣稱自己是包含所有集合的集合。因此V必然會有如下這種形態:
V= {a, b, c, d, e, … , V, x, y, z, …}
按照道理,宇集內部那個V(我們已經標成紅色)跟外面那個V是一樣的,因為宇集既然是宇宙間所有集合的集合,那它就是最大的集合,所以必然只有唯一的一個最大集合。因此:
V = {a, b, c, d, e, … , V, x, y, z, …}
把這個紅V套上去就應該是底下這種樣子:
V= {a, b, c, d, e, … , {a, b, c, d, e, … , V, x, y, z, …}, x, y, z, …}
而更裡面那個標紅的V也必定是複制了同樣的形態:
{a, b, c, d, e, … , V, x, y, z, …}
像這樣無窮無盡層層疊疊複制下去,永無盡頭。
頭被搞暈了吧?這樣的怪物到底是甚麼?雖說這樣的造形讓人頭暈目眩,但我們還是沒有充分的理由說它不存在。要如何證明它存在或不存在呢?如果你懷疑這樣的集合不存在該怎麼做呢?有一個很符合邏輯的想法就是,既然V「揚言」自己是所有集合所成的集合,那如果我們能夠製造出一個集合,然後證明它不在V裡,不就拆穿V的牛皮了嗎?但去哪裡找這個集合呢?
俗話說踏破鐵鞋無覓處,忽然想起一個老朋友R = { x 〡x ∉ x},它不就是在《公設化集合論的奧秘 (3)》裡所談到的羅素詭論集合嗎?我們將其稍加改裝成為如下集合:
B = {x ∈ V 〡: x ∉ x}
這個微小的差異在於現在有個號稱包含一切集合的V,那麼任何集合都必須是它的成員才行,所以有x ∈ V這個條件。我們還可以接著問,B集合是它自己的成員嗎?如果是的話,那麼B ∈ B,則B必須符合上述集合的條件,也就是B ∈ V且B ∉ B
把它寫成數理邏輯式就是:
(L1) B ∈ B ⇒ (B ∈ V) · (B ∉ B) (其中黑點為and的意思)
反過來說,如果B ∉ B,那麼根據假設,V包含一切集合,所以B ∈ V,這樣的話B剛好又符合集合B = {x ∈ V 〡: x ∉ x}的條件,所B ∈ B。
整理成理邏輯式就成了:
(L2) (B ∈ V) · (B ∉ B) ⇒ B ∈ B
把(L1)和(L2)組合起來可以得到一個雙條件句:
(L3) B ∈ B ⇔ (B ∈ V) · (B ∉ B)
學過一點數理邏輯的人都知道,符號⇔兩邊的邏輯語句等值,也就是兩邊必須同為真或同為假整個邏輯式才能成立。但由於B ∉ B是B ∈ B的否定,所以它們必定一真一假,那麼邏輯式 (L3) 為真的唯一希望就是B ∈ V為假了。因為若B ∈ V為真,那兩邊的另兩個語句永遠一真一假,(L3) 就永遠沒有成真的希望了。因此根據邏輯,我們得出B ∈ V為假,也就是B ∉ V。
這個結論的重要性在於既然有一個集合B不在V裡,那表示V根本不是包含一切集合的集合,牛皮終於吹爆,詐騙案宣告偵破。換句話說,那樣的集合V並不存在。
因此宇集V和羅素集合R一樣,都會導致邏輯矛盾,因此都成為公設化集合論「掃黑」的對象。在集合論發展的過程裡,對於排除這種搗蛋分子有兩條路線,一個是我們一開始採用的ZF集合論,它直接將這種龐然怪物趕出集合的園子,塑造了一個純淨的理念世界,其中只有一種物件(集合)和一種關係(∈),不需要其他多餘的材料。
ZF系統如何處理羅素詭論我們已經在《公設化集合論的奧秘(4)》裡談過了,現在簡短介紹一下另一條路線的主要系統NBG如何面對這種邏輯困境。所謂NBG是這個系統的三個主要貢獻者的名字縮寫,這個陣容也是夠嚇人的。N是被稱為神童的電腦之父馮·紐曼(John von Neumann),B是瑞士知名數學家伯納斯(Paul Bernays),證明論的現代奠基者根岑(Gerhard Gentzen)就是他的弟子,G不用說就是大名鼎鼎的哥德爾。
NBG系統的最大特徵是它用類(class)來函蓋所談論的理論對象,集合是類的一種,而那些不屬於集合的V和R則稱為真類(proper class),但在ZF系統裡是不談論真類的,所以在進入NBG系統之前必須先定義好集合和真類以免混淆。一般用M(X)來代表X是個集合,用邏輯表達式(∃Y)( X∈Y)來定義。它的意思是說如果X是集合,那它可以被登記在另一個集合之下成為它的成員。但真類無法這樣,所以它的定義就是M(X)的否定(寫成¬M(X)),因為它們無法被登記在任何集合之下成為成員,所以真類不是集合。或者換個說法,如果一個類可以登記在其他集合名下,那這個類就稱為集合,如果不可以登記在任何集合名下就稱之為真類。
按照這個新規定,我們發現之前為宇集V所做的造型
V= {a, b, c, d, e, … , V, x, y, z, …}就不能存在了。
首先紅V沒有資格登記在任何集合名下,況且外邊那個V(當然是同一個V)也不是集合,兩個集合的條件都不符合,在這種裡外不是人的情況下,我們之前對宇集那令人頭昏腦脹的構造方式瞬間煙消雲散,好似鬼魅夜間幻化的亭台樓閣到了白晝只剩下荒草間的荒塚。
雖然NBG理論系統可以合法談論真類,算是一種擴張了的類理論而不僅是集合論,但從集合和真類的定義(也就是M(X)和¬M(X))可以知道,類並不是集合。所以在集合論的領域裡,兩者並無本質差異,也就是NBG並沒有因為加入真類而推導出某些ZF所沒有的定理。
由於真類會在集合系統裡引發邏輯矛盾,所以NBG將其納入並非改變或擴展集合的定義,只是一種權宜之計。它認為在探討一個理論時,若給「非集合」一個代表符號則能增加理論符號系統的表達力,對理論探索來說不見得是壞事。正如聊齋裡談到很多鬼靈精怪的故事,它給我們增加了許多生活的樂趣,但不表示這些名稱所說的東西就真的存在。
僅管NBG有那麼強的卡司陣容和理論表達力,但在集合論領域的普及程度卻趕不上ZF,其中一個原因還是在於理論的簡潔和美感。ZF集合論讓你看到一個純淨而單一的世界,裡面沒有塵土只有琉璃和寶石,沒有魑魅魍魎只有潔白的柏拉圖地磚。















![Christmas Tree, Bokeh Version [362/366]](http://pansci.asia/wp-content/uploads/2015/03/8317397452_98b547512e_o-1-350x525.jpg)