公設化集合論的奧秘(11) 探索神奇的實數尺寸

credit:pixabay.com

文 / 翁昌黎（《孔恩vs.波普》中文譯者）

想像你在一個一望無際的沙灘，晶瑩的海岸由近乎純白質地的細沙構成，在陽光下閃爍著寶石般的光輝。天空有一條發出橙色亮光的細線，似有似無，那是柏拉圖世界裡的實數線投影到這個神奇星球的擬似影像。

假設每顆沙粒代表一個集合，將這些沙粒灑向這條實數線企圖將它填滿，你會發現這些純白的細沙集合像是消失了一般，完全不影響橙色實數線的顏色，因為沙粒實在太稀少了。

就算你得到一種魔法，能在瞬間將這些無窮沙粒悉數灑在數線上，可是實數線上依然觀察不到白沙的蹤跡，因為它們仍然太過稀少。我們再度向孫悟空的師父菩提祖師求救，請他老人家傳授一個厲害點的法術，可以將剛剛灑出去的每一粒沙都變成等同於這個無窮沙灘世界的所有沙粒。但你將失望地發現，雖然親眼見識了菩提祖師將一沙粒化成無窮沙數世界的絕活，可是實數線上卻依然沒有任何一點斑白的痕跡，就好像這些從無數再化成無數的沙粒憑空消失一樣。

這到底是怎麼回事？理由是它們仍然太過稀少，所以無法蓋住實數線，甚至無法顯示出它們的存在。如果我們能夠把無窮顆沙粒集合和實數線投射到我們這個時空，那你所看到的場景大概就會有如以上的描述，可數無限顆沙粒再變現出可數無限顆沙粒的總合對於實數線來說依然是杯水車薪。

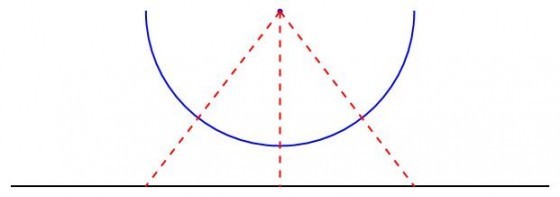
為了證明整個實數集合確實比可數無限集合還大，我們先來觀察一個現象：把（–1, 1）這個實數開區間彎成半圓形，如下圖藍線部分所示。假設藍線左邊的端點是–1，而右邊的端點是1，垂直的紅虛線劃過的點是原點 0，所以垂直紅虛線的左半邊正好是負實數而右半邊則是正實數。

從虛擬的圓心處往黑色實數線用紅色虛線連接，你會發現每一個區間（–1, 1）內的數都正好對應到黑線上的另一個實數。而當虛線接近水平線時，左右兩邊對應到黑色數線的絕對值就會變很大，且所對應的實數越來越趨近於（–∞, ∞）。因此（–1, 1）區間內的實數和（–∞, ∞）區間內的實數（等於是R）有一對一且映成的關係。那麼根據定義，（–1, 1）區間裡的實數與全體實數R等量。

假設區間（–1, 1）中所有實數的集合為I，則基數〡I〡=〡R〡，也就是說區間（–1, 1）裡的實數個數與所有實數集合的個數一樣多。以上這個方法稱之為幾何學證明。雖然直觀上沒有問題，但站在集合論的立場，我們應該要想有沒有更嚴格的數學證明呢？這下可傷腦筋了，根據我們目前的數學知識配備，若要證明〡I〡=〡R〡，則需要找到一個從I到R的一對一且映成的函數才行。那麼到哪裡去找這麼個函數呢？

正所謂眾裡尋它千百度，驀然回首那傢伙就在正切函數（tan）處。我們發現當tan的x值趨近於–π/2時，它的y值會向–∞逼近，而當tan 的x值趨近π/2時，它的y值會向∞逼近，而且任何一個x值只對應到一個y值。這不就是說正切函數tan在（–π/2, π/2）與全體實數R之間形成一對一且映成？tan：（–π/2, π/2）→（–∞, ∞）不就是夢寐以求的答案？

但剛剛的幾何證明說的是（–1, 1）→（–∞, ∞）有一對一且映成函數而不是（–π/2, π/2）→（–∞, ∞），眼看就要得手了卻差一步，該怎麼辦呢？只要設法把（–π/2, π/2）變成（–1, 1）不就好了？但我們的野心還要大一些，我們希望把（–π/2, π/2）→（–∞, ∞）的函數變成（0, 1）→（–∞, ∞）的函數，理由待會兒馬上會揭曉。

這個函數首先要把（0, 1）區間裡的每個x轉變成（–π/2, π/2）區間裡的某個y，但因為tan(y)就會把每個y從（–π/2, π/2）映射到（–∞, ∞），因此我們要找的函數就是某個用x來表達的正切函數，我們發現經由線性變換可以找到這個函數。既然我們想把某個（0, 1）區間裡的x變成（–π/2, π/2）區間裡的某個y，於是問題相當於把某個（0, 1）區間裡的x轉換成π/2 (–1, 1)區間裡的某個y，它們的關係式是：

π/2 (a x +b) =y

我們先把π/2提出來，待會兒再放回去，計算上會方便很多，因此：

當x = 0的時候 y= –1，代入式子得到b= –1

當x = 1的時候 y= 1，代入式子得到a= 2

把a和b的值放回關係式得到π/2 (2 x–1) =y 。

就是它了：函數 tan[π/2 (2 x–1)] 可以把（0, 1）區間裡的實數一一對映到所有實數，因此我們用數學分析的方法證明了（0, 1）區間裡的實數和整個實數一樣多，比剛剛的幾何證明方法又進了一步。

這個結果夠驚人的了，這麼小段的（0, 1）區間裡的實數居然和整個R一樣多，但我們更想進一步知道R是否也是可數無限？對於這個問題康托總共給出兩個完全不同證明方法，第一個是在1874年提出的，其中用到集合的排序和有界（bounded）的概念。第二個證明直到1891年才提出，採用的正是康托拿手的對角線證明法，我們就再次來看看康托如何拿這項精妙的數學武器來對付巨大的實數尺吋。

因為剛剛已經證明了R和區間（0, 1）等量，所以只要證明（0, 1）區間裡的實數是否可數就等於證明了R是否可數， 這大大簡化了我們的工作，剛剛些許辛苦還是值得的。由於這個區間內的實數都能用無限小數的展開形式來表示，假設它們的個數是可數的話，那我們就能將區間裡的實數編上序號，比如：

r₁ = 0.320059874…

r₂ = 0.912533121…

r₃ = 0.007213568…

r₄ = 0.552418792…

r₅ = 0.778451420…

r₆ = 0.118841234…

r₇ = 0.665590012…

…

…

需要注意的是，由於0.99999…等於1，所以在這個可數無限序列裡0.999999…的寫法被排除掉。

現在我們用一種特別的方法來製造一個新的實數x，那就是對任何小數點之後的數進行改裝，凡是遇到1就把它改成2，凡是遇到1以外的數（比如0, 2, 3, 4, 5, 6,  …）就把它改成1。我們拿以上的實數序列作例子，依次取小數點後面的第1, 2, 3, 4, 5, 6, …位，也就是按照對角線的方向來進行改造。

我們看到r₁小數點後的第1個位數是3（如紅色數字所示），所以依照規定將其改成1，r₂小數點後的第2個位數是1 ，所以依照規定改成2。依此類推，我們得到一個新的實數

x = 0.1211121…

這個數字的特點是它不同於r₁，因為小數點後第1位數不相等，它也不等於r₂，因為小數點後第2位數不相等。依此類推，我們依照此法製造出來的數字x不等於任何序列中的數字。但它明明是（0, 1）區間裡的實數，所以與一開始的假設相矛盾。我們得到（0, 1）區間裡的實數是不可數這個結論，因此，實數R也是不可數的。

原來，R的個數比可數的N和Q都要來得大。於是一個疑問自然浮現：在《公設化集合論的奧秘 (7)》一文裡，我們也是用對角線法證明了全體自然數N的冪集合P(N) 的元素個數同樣是不可數，那麼自然數冪集合的基數〡P(N)〡是否等於實數的基數〡R〡呢？ 這兩種不可數集合其尺寸會一樣大嗎？我們又如何知道它們是否有相同的尺寸呢？這些問題只有等下回再分解囉！

「空虛寂寞覺得冷會傳染嗎？」「為什麼人看到可愛的東西就想捏？」「為什麼蚊子喜歡叮穿深色衣服的人？」

科學從不只是冷冰冰的文字，而是存在世界各個角落熱騰騰的知識！不論是天馬行空的想像或日常生活的疑問，都可能從科學的角度來解釋。

本月的泛科選書 《不腦殘科學2》是泛科學作者編輯團隊嘔心瀝血的超級鉅獻！不只能滿足大人與小孩的好奇心，更將拓展你的視野，帶領大家發現一個嶄新的世界！

泛科限時優惠79折(含運)，現在就帶一本回家