你知道有那麼一條公式——它不僅可以表述生態系中動物族群的數量變化、城市裡人口隨時間的變遷,還與金融市場的波動、甚至是氣候變遷有所關聯?更令人驚奇的是,這個式子並不是什麼複雜的偏微分方程,它只有短短一行、就連國小學生都能代入算出。
這個看似相當簡單的式子,能推演出極其複雜的圖像;而在看似錯綜複雜的圖像背後,卻又隱藏著某種未知的神秘規律。今天這篇文章,將帶領大家透過這個簡單的函數重新認識世界。
自然界潛藏的規律
且讓我們先從自然界談起。假設一片草原上有一群斑馬生活著,我們想要知道明年、後年、甚至數十年後的數量;我們知道,這一部分取決於斑馬的出生率,還有另一部分取決於環境的負載力——假設斑馬的族群總數超過了該草地所能負荷的程度,很可能在往後導致族群的縮減,因此,負載力有點類似於一個約束條件。有了以上的資訊,我們可以嘗試用數學來描述:
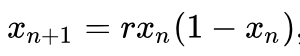
這邊,xn 代表的是「現存族群數量與最大可容納的族群數量」之比值,你可以想像成:假設這片草原此時此刻有 60 隻斑馬,而草原所能容納斑馬數量的最大值為 100 隻斑馬——一旦超過這個值,那麼便會面臨諸如饑荒等生態危機。因此,在此例子中,x0 = 60/100 = 0.6。而假設我們想知道明年的數量,也就是 x1,便可以帶進去推算。那麼,式子中的"r"又是什麼?你可以將它理解為「成長率」,但要注意的是,它的值一般是界定在 0 與 4 之間。
如果單純只看 xn+1 = r xn,假設 r=2,今年有 60 隻斑馬、明年有 120 斑馬、後年便會是 240 隻,這樣只會無止盡地指數增長下去;因此,當我們設定了"(1 - xn)"這個約束條件後,便可以解決這個問題——假如今年的 xn = 1,意味著該地斑馬數量已然達到環境可負荷的最大值,便會因為饑荒等因素滅絕,隔年得到的數量便將為零。這個看似簡單、卻又多少能給生態學家建構模型的公式,稱為「單峰映射」(logistic map),也是今天文章的主角。
這個式子不僅可套用在生態系,也可以套用在人口學:舉個例子,某城市今年有 60 萬人,該城市所能負載的最大人口為 100 萬人,而每年的成長率大概是 r = 1.5,那麼,套進公式會發現:明年的人口將為 36 萬、第三年人口將為 34.6 萬……,從而漸漸達到平衡點。如果一開始我們假定有 30 萬人,明年將會成長為 31 萬、後年成長為 32 萬,然後趨近於和前者相近的平衡點。最後,如果這個城市一開始就有 90 萬人,第二年便會因為環境負載力而銳減至 13.5 萬人,但後年、大後年之後將會隨著成長率升高而回升至約莫 33 萬人的平衡點。
而這些資訊並非憑空構思的,因為它們本身就含括在單峰映射的公式裡,用圖表呈現便一目了然,你會發現無論前幾年如何變化、最終都會回歸一個平衡點:
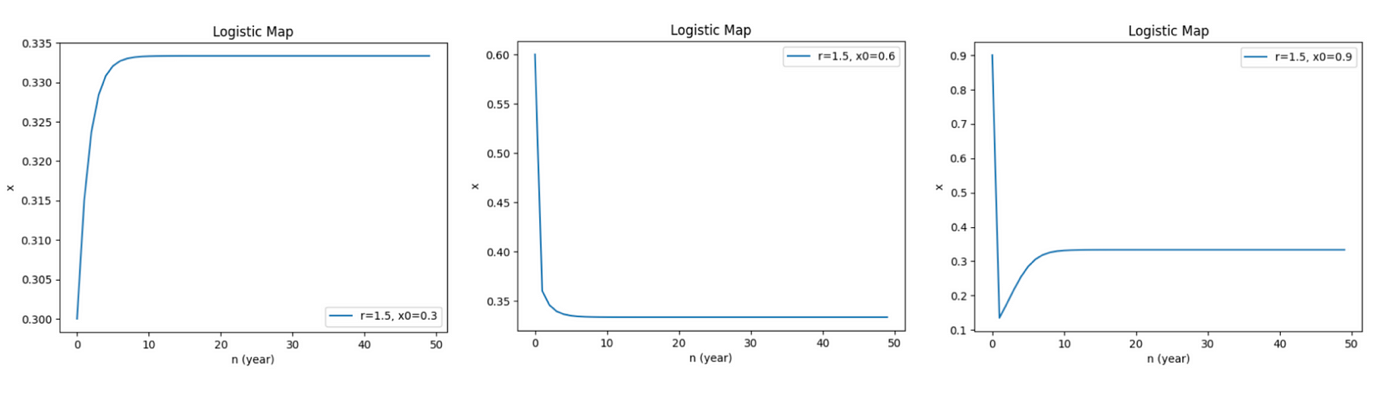
而這個穩定值是取決於"r"的,也就是說,只要 r = 1.5,無論人口數目如何變化,最終的平衡點都不會有所差異。
規律的瓦解、未知的開端
因此,我們何不來看看"r"會如何變化?這時,我們回到原本的假設:一個城市裡有 60 萬人口,如果改動不同的 r,演化曲線將會如何改變?
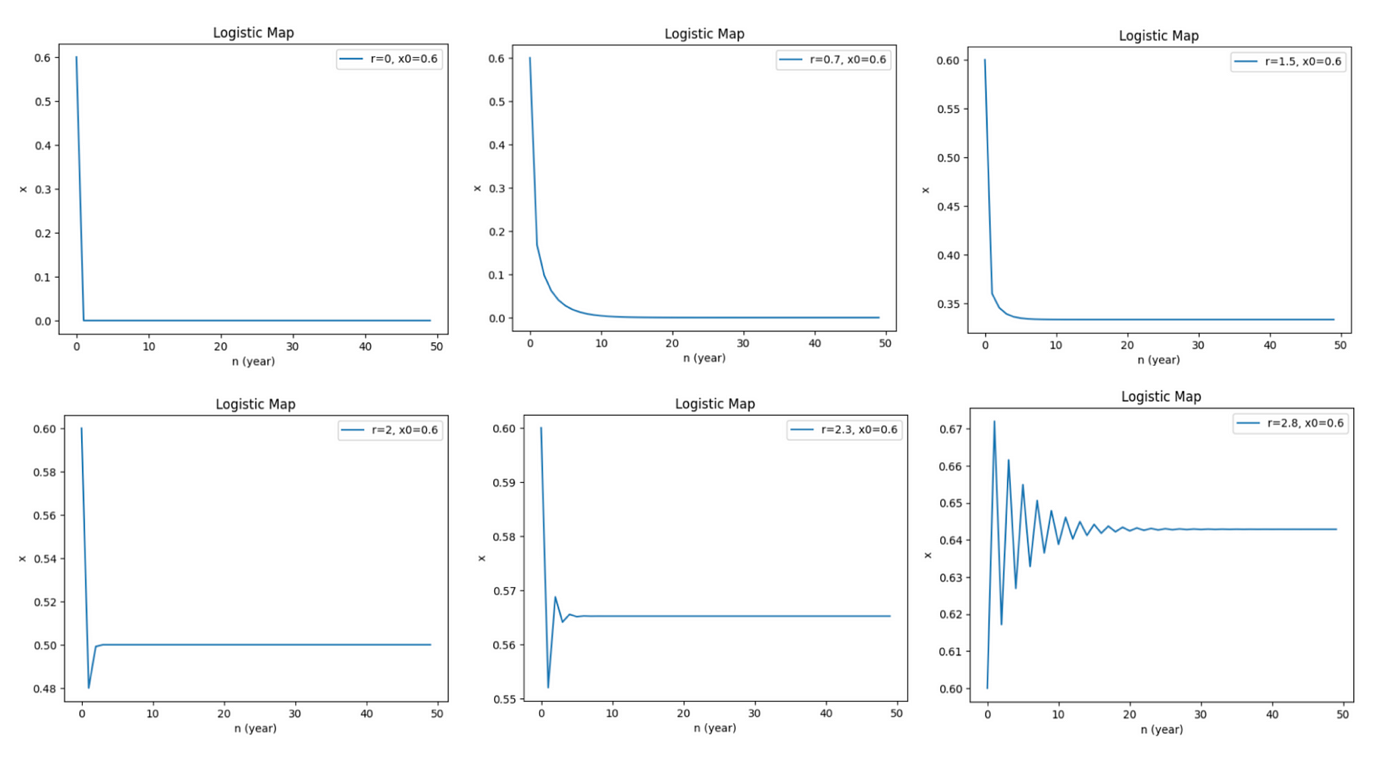
當我們將 r 值逐步增加,一切看似並無異常;當 r=2.8 時,我們發現圖形出現了週期性的振盪,但最後依舊回歸平穩。順帶一提,我們可以藉由「分枝圖」(bifurcation diagram) 來觀察 x 的穩定值與 r 的關係,在 r=0 至 2.8 之間,x 穩定值有攀升趨勢;在 r=1.5 時,根據前述的例子,x 的穩定值落在 0.33 左右,從下圖也可以直接看出:
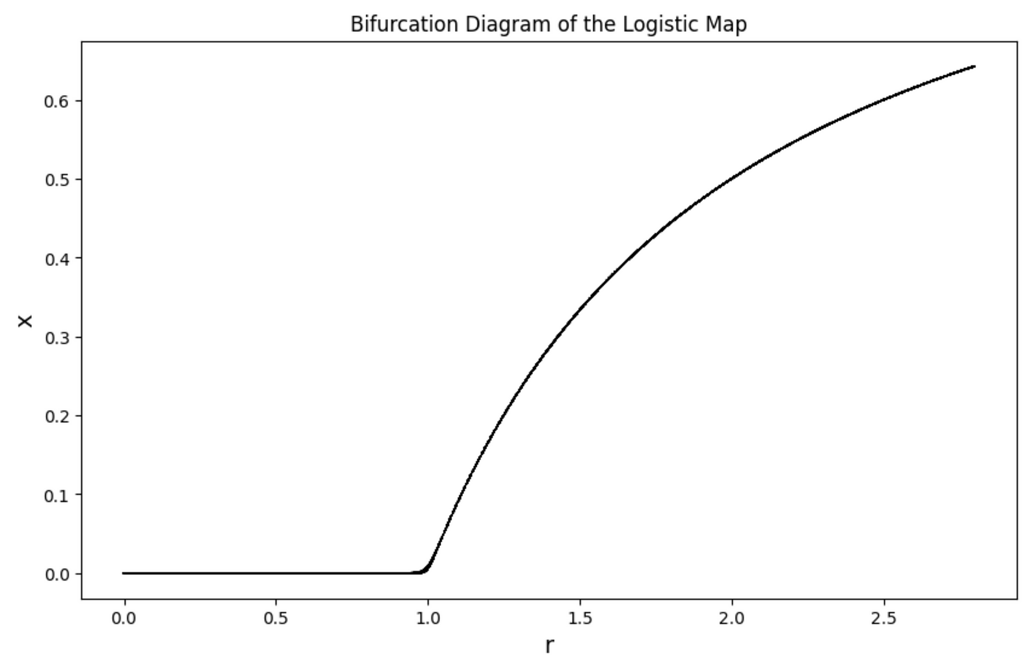
我們繼續調大 r 值。正當一切看似正常發展時,詭異的事情發生了:
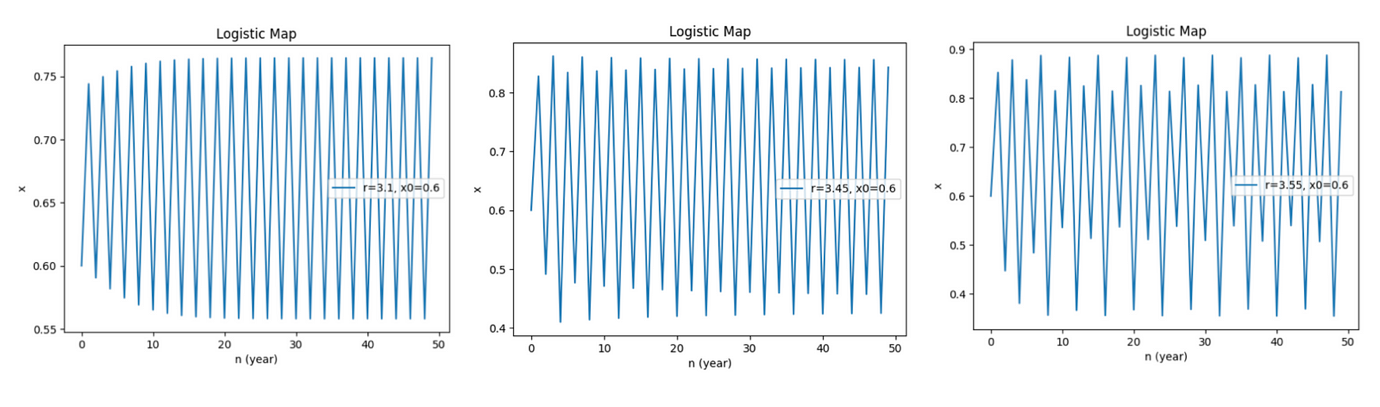
在此之前,一切族群的數量都是平穩的,但在 r 超過 3 左右,持續的振盪出現了,且自此「平衡點」不復存在;不僅如此,當 r 值不斷調升,顯示出來的圖像從原本 2 個值、4 個值、到更多值之間來回振盪。值得一提的是,這種「週期性振盪」的現象在生態圈與人口變化中是確實存在的,很有可能前一年數量減少、今年數量增加、明年數量又再減少。讓我們來看看對應的分枝圖:
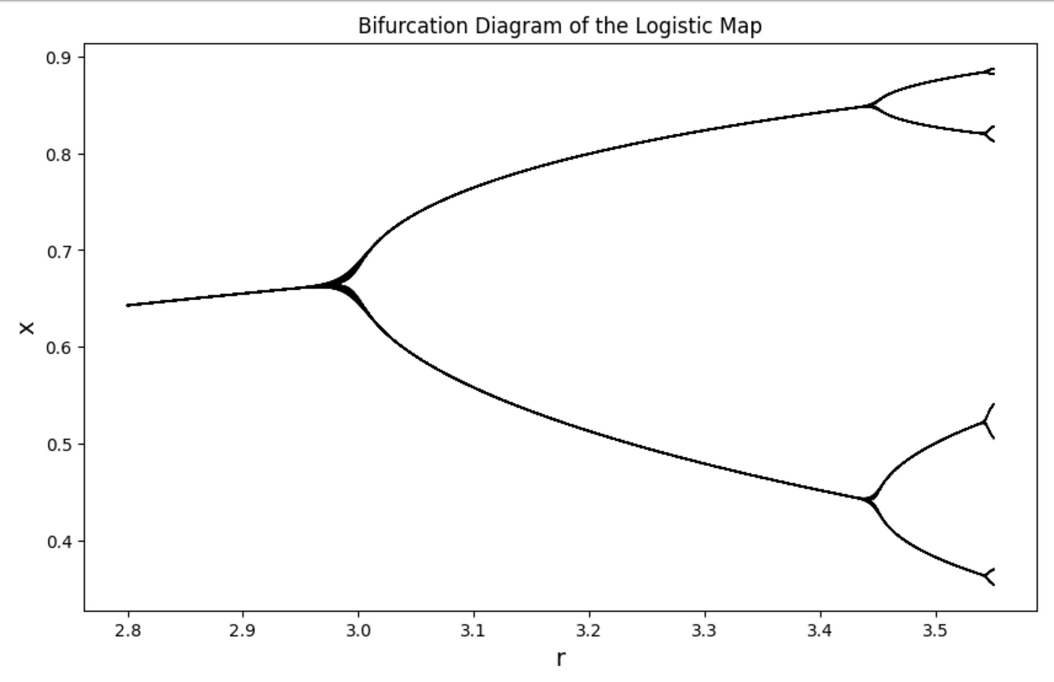
這對應於原本從 2 個值之間的擺盪、分岔成 4 個值之間的擺盪、再分岔成 8 個值之間的擺盪……如此往復。此外,如果你留意橫軸 r 之間的間隔,會發現:當 r 愈大時,分岔的速度也愈快!
現在讓我們繼續將 r 值調升,來看看會發生什麼事:
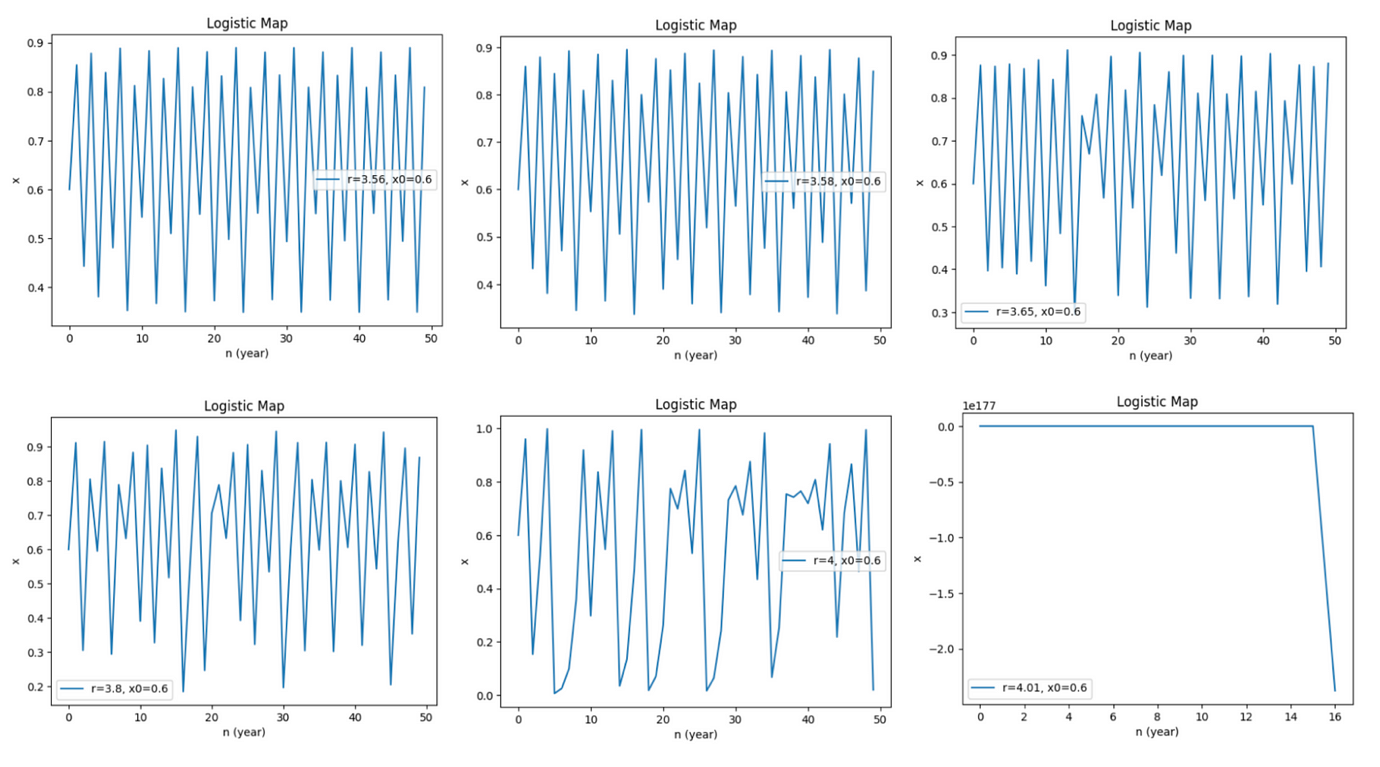
話不多說,我們直接來看看分枝圖:
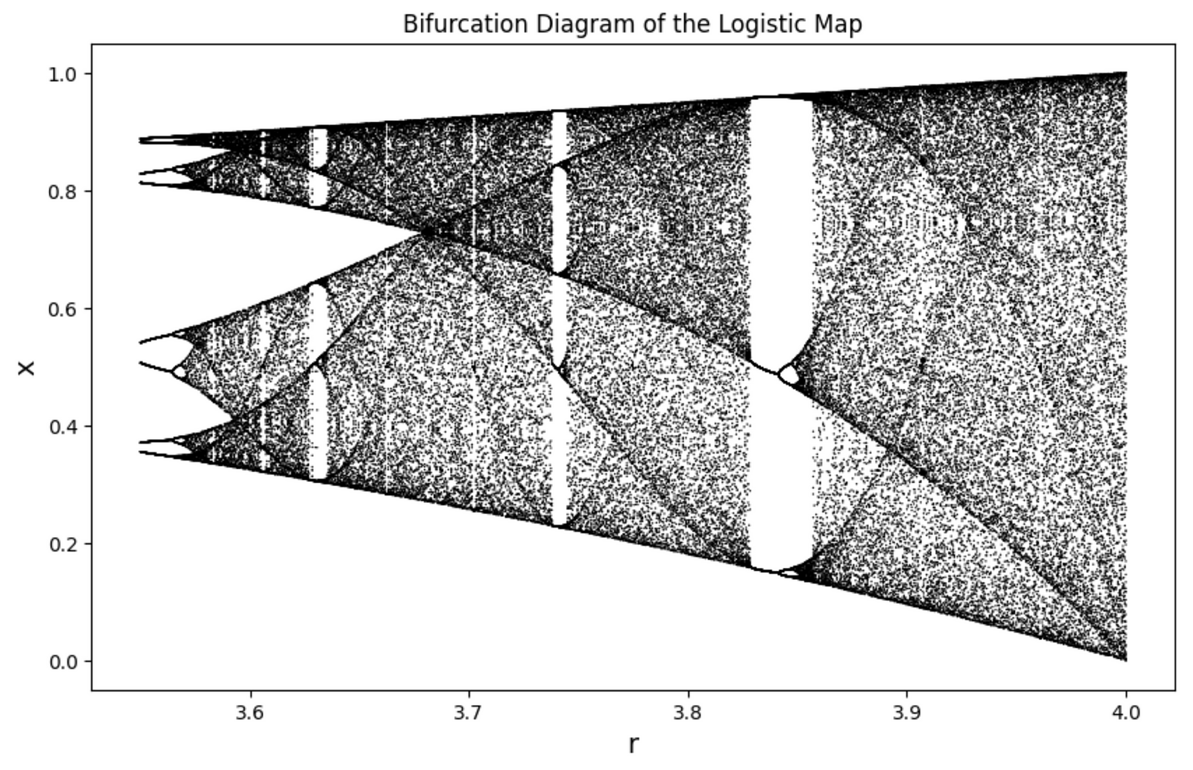
令人毛骨悚然的結果出現了!前面我們觀察到,當r提升時,系統會出現週期性的振盪,對應於分枝圖中的「分岔」,且分岔的速率會不斷增快、再增快;而在 r 超過 3.5699 時,規律的振盪、分岔將不復存在,取而代之的是一團無法預測的隨機——這就是所謂的「混沌」(chaos)。
混沌、股票市場、以及蝴蝶效應
現在讓我們看一下完整的分枝圖長什麼樣子:
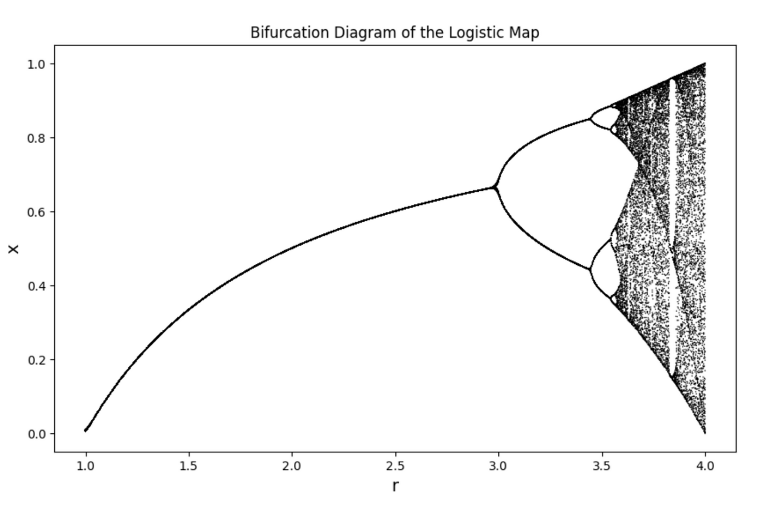
換而言之,當系統的變量到一定程度時,將會變成隨機且無法預測的。以人口為例,一開始我們假設的情況很簡單,就是 60 萬人口與 r=1.5 的成長率;接著我們發現,無論人口基數如何,只要 r 維持原狀,數年、乃至於數十年後的平衡點都是相近的。然而,當r值提升後,平衡點的值便會浮動了,r=3 之後週期性的振盪便出現了、且分岔點不斷加速倍增;緊接著,我們赫然發現:
當 r 值大於 3.5699 時,系統將全然處於混沌狀態。
也就是說,即便給定初始條件,最後的人口演化將會是無法預測的。事實上,這種「混沌」、「隨機」的現象並不僅僅侷限於自然界的族群或者人口數量,它其實是隨處可見的。比如:家中水龍頭關不太緊時,水滴很自然地會落下,按理來說,鬆緊程度與水壓毫無變化的情況下,滴水的規律應該也是不變的;但如果你花一段時間觀察,會發現水滴可能一下子連續落下兩滴、一下子又只落下一滴——我們根本無法預測每一次的滴落模式。
另一個例子就是金融市場:當我們投資了固定金額的股票後,市場的波動將導致金額的浮動,就算有再好的分析師與預測模型,我們也不可能精準預測明天的投資金額會變多少。順帶一提,在金融學中描述期權的模型是「布萊克-休斯模型」(Black-Scholes model),它便是從微觀粒子的「布朗運動」(Brownian motion) 所推導而來,其中粒子碰撞隨時間演化的隨機過程被稱為「維納過程」(Wiener process)。布萊克-休斯模型的假設之一,便是將隨時間演化的「股票價格」描述成維納過程,從而預測、消弭潛在的風險。事實上,休斯本身大學時就是主修物理學的。
而提到「混沌現象」,最經典的例子當然還是氣象學家愛德華.洛倫茲(Edward Lorenz)的那句名言:
「一隻海鷗拍動翅膀,將導致永久性的氣候變化。」
“One flap of a sea gull’s wings would be enough to alter the course of the weather forever.”
爾後,這個現象被稱為「蝴蝶效應」(Butterfly effect),也就是說,縱然系統初始條件只有微不足道的變化,也會導致最後產生的結果大相徑庭;即使是一隻在巴西的蝴蝶拍動翅翼,周邊的氣流變化會連帶影響、擴散至大氣系統,甚至能致使一個月後的德州發生龍捲風。
這些非線性、隨機的現象在自然界無處不在,許多科學家也嘗試研究,締造了「混沌理論」(chaos theory) 的研究熱潮。一旦我們能從中梳理出一些規律,那麼,也許便能更精確地掌握「混沌」之中的資訊,這將有助於我們更精確地預測投資股票的風險、也有助於人們更準確地預測天氣的變化。
混沌背後的神秘常數
從描述族群、人口的簡單函數推演到「混沌狀態」的存在已經夠令人驚豔了,然而,不知你是否曾留意過分枝圖中、每一段分岔點之間的間隔?
如果你把我們最後得到的分岔圖放大來看,會發現在混沌狀態之前、分岔點出現的速率不斷增快;而如果你對每一個分岔點之間的間隔取比值,你會發現——每一次得到的值都會是同一個數字,這個數字大致為 4.669,它被稱為「費根鮑姆常數」(Feigenbaum constants)。
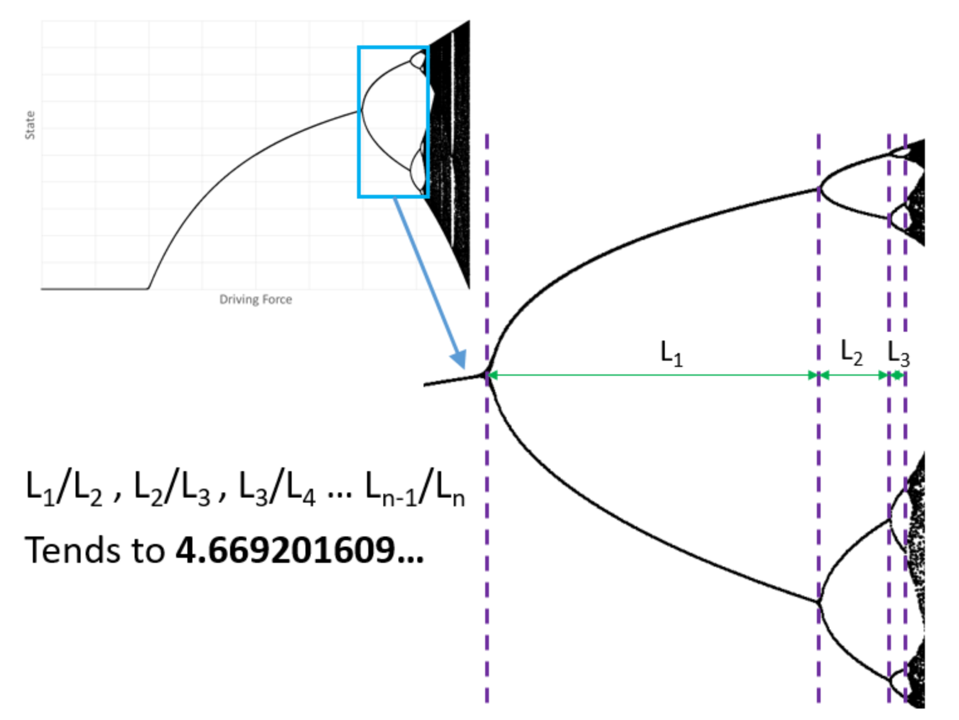
更令人細思極恐的是,這個「常數」並非只存在於單峰映射,所有混沌理論中有這種分岔性質的圖像,它們之間的比例都是這個常數!而目前數學界尚未能明確理解這個常數的性質,唯一可以推測的是:
費根鮑姆常數(4.669…)與混沌理論有密不可分的聯繫;該常數的出現意味著混沌現象即將發生。
在前述單峰映射的例子中,費根鮑姆常數主宰了 r=3.5699 之前的分岔規律;在 r 超過 3.5699 後,系統便徹底進入混沌狀態了。
除此之外,你或許也發現了,每個分岔的形狀都超乎尋常地相似,後一個分岔根本上就是前一個分岔的縮小版。這種特徵令人聯想到數學上的「碎形」(fractal),也就是某些形狀放大後會是自己的本體、從而無窮延伸下去。最著名的例子就是複數平面上二次多項式迭代出來的「曼德博集合」(Mandelbrot set)。信不信由你——當我們將單峰映射的分枝圖與曼德博集合比照來看,會發現分岔點之間是有所對應關係的;也就是說,單峰映射可以視為曼德博集合的一部分!
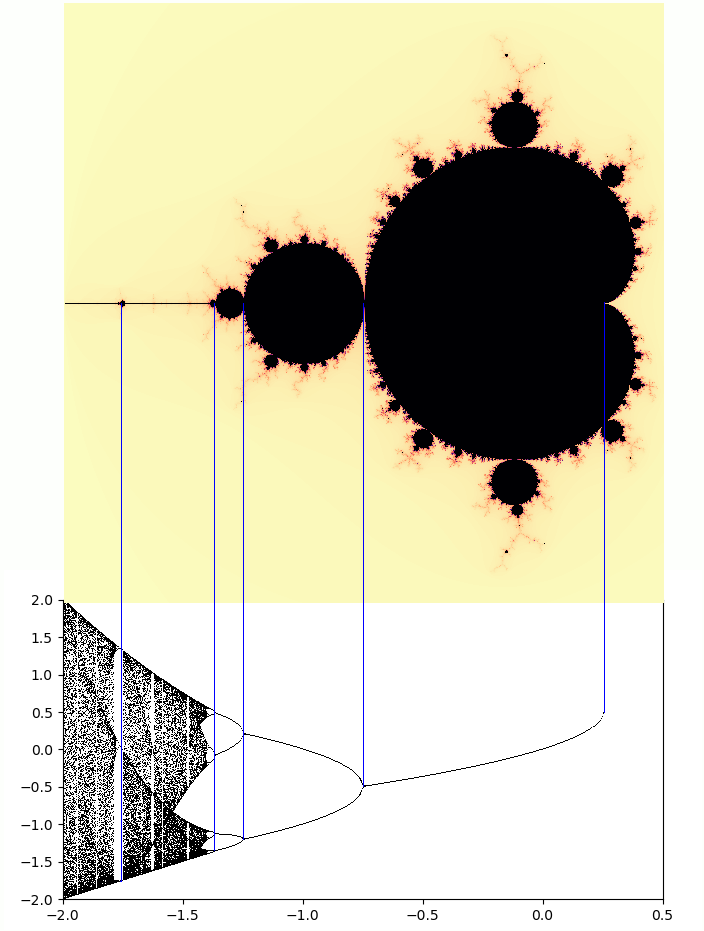
從簡單的單峰映射公式,我們推導出了自然界族群、人口的演化模式,進一步發現了「混沌」狀態的存在;而在看似極其複雜的混沌狀態中,似乎又發現了隱藏在隨機背後的神秘規律。
混沌理論在生活中是無所不在的,時至今日,仍有不少未知的特性等著人們發掘與驗證。從生物的競爭、人口的演化、股市的浮動、亂流的成因、到氣候的變遷……這些日常事物都被混沌現象主宰著,從而使我們無法精準預測到未來的走向。然而,費根鮑姆常數的發現與幾何碎形的聯繫卻也指出了隨機背後潛藏著某些規律,這也不禁令人讚嘆自然界的美麗與神秘。