文長,非常長,但希望藉此文能更簡單、更清楚的說明天氣預報的難處、如何去看天氣預報的不準確,才是對預報的應用更重要的。
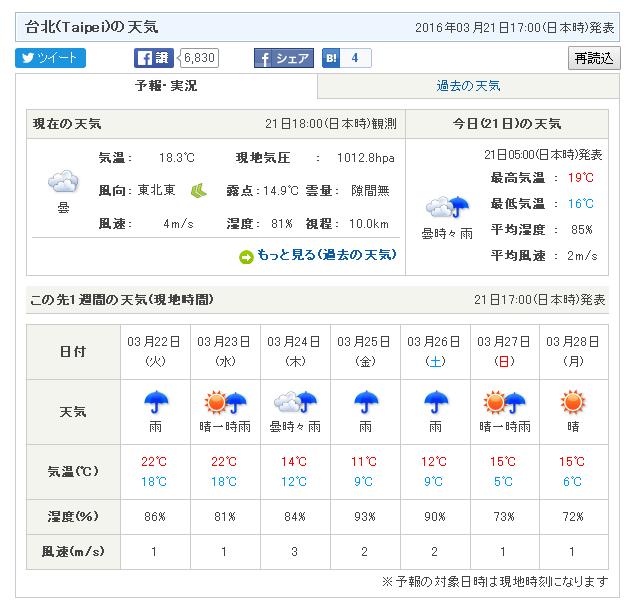
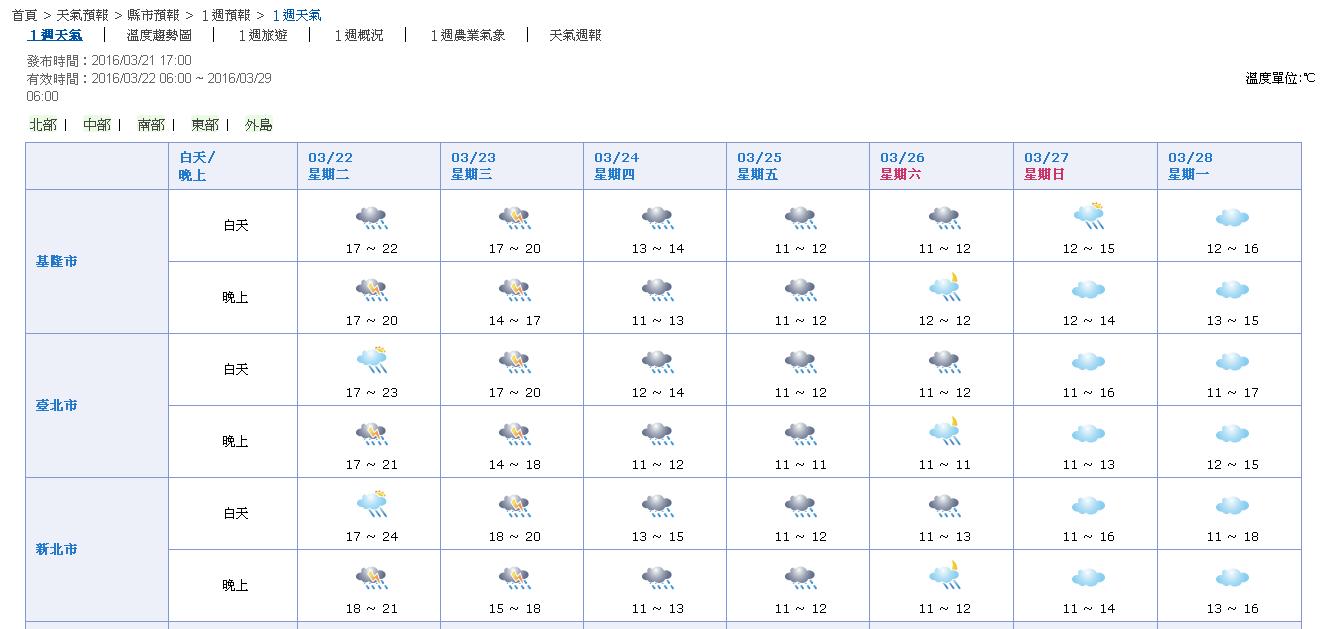
我們先看一下3/21氣象局和日本氣象協會的一周預報:
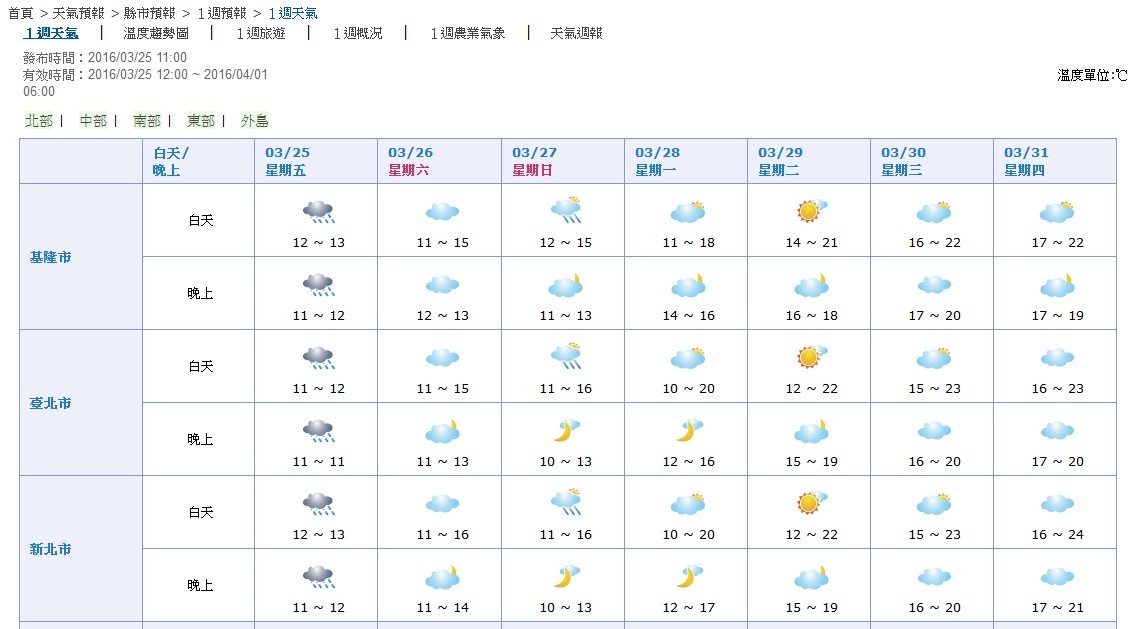
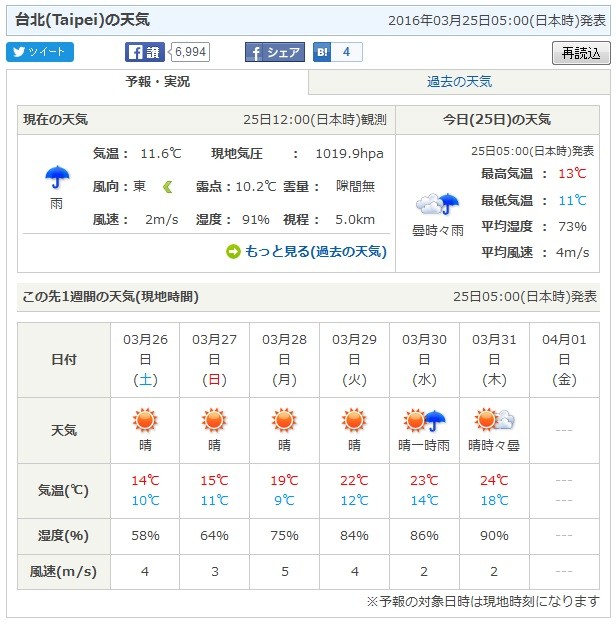
再看3/25的預報結果,日本氣象協會的預報(溫度部分日本有明顯修正,降雨方面是兩邊都有修正調整):
這次中央氣象局預報比日本準了,但其實……
當不夠理解氣象預報時,比較是沒意義的
接著在心情不好、天氣不好又遇到報不準的時候,就會罵氣象局。
「為什麼氣象局總是報不準?」「不是說會下雨嗎?怎麼只下兩滴就沒了?」「我乾脆看日本的預報好了!」「氣象預報本來就該準不是嗎?不準怎麼不會檢討?」
無論今年一月、三月氣象局與日本氣象協會針對寒流與冷氣團預報結果的落差,或是三月時氣象局幾次對鋒面降雨時間判斷的誤差。從媒體打臉來打臉去的渲染,以及網路上的輿論,我特別注意到了兩個常見的氣象預報迷思:
- 對氣象預報原理誤解進而提出不合理的批判(多數是認為「準是應該的」)。
- 資訊不對稱,或許是對氣象預報知識的不足,使得報導或是許多民眾只能聚焦在媒體、網路、氣象局之間的口水戰。
其實,只要再深再細一點的探討分析,再加入一點氣象知識,即使不具備氣象專業背景,多少也能看出以下的盲點:
不準是什麼意思?
不準的定義是指前一天的預報還是一週的預報,就算拿前一天預報來說好了,一年 365 天中,有幾天有預報成功有幾天失準?然後一年幾天失以上準叫做預報很糟?還是就不管反正遇到幾次不準就是不準?這樣的話我倒覺得這比較像是「認知偏誤」。
氣象科學是門複雜的應用科學
在不理解數值如何產生的情況下,拿不同預報的結果來直接比較,沒有什麼科學意義,真的要認真比較的話,起碼要像上面說的要每一天、針對特定結果如溫度之類的做統計比較,但這實在對於預報本身沒什麼幫助,因為數值預報除了統計還得考量學理,而大氣科學是門不太容易研究的應用科學(結合物理、化學、流體等知識)。
百分之分準「甘有可能」?
如果你只能接受「只要告訴我,下雨或不下雨、冷還熱,不要說什麼 40% 降雨機率、最高最低溫……」的話,我想觀落陰比較快?不是啦,我指的是若只能接受百分之百準的預報,未免太強人所難了。
如果你願意繼續看下去,那我就來細說國高中不教、主流媒體少講、人們不常聽到的「關於天氣預報」!
沒有百分之百準的氣象預報
過去有好幾篇在不同平台的專業解說文章[註1],這些文章的共通點就是在說明氣象預報為什麼不準?不過我想,既然是會覺得氣象局的預報總是失準的人,或許也會認為,每當預報發生失準時,氣象預報人員總是會拿勞侖茲的「蝴蝶效應」來作為塘塞之詞。
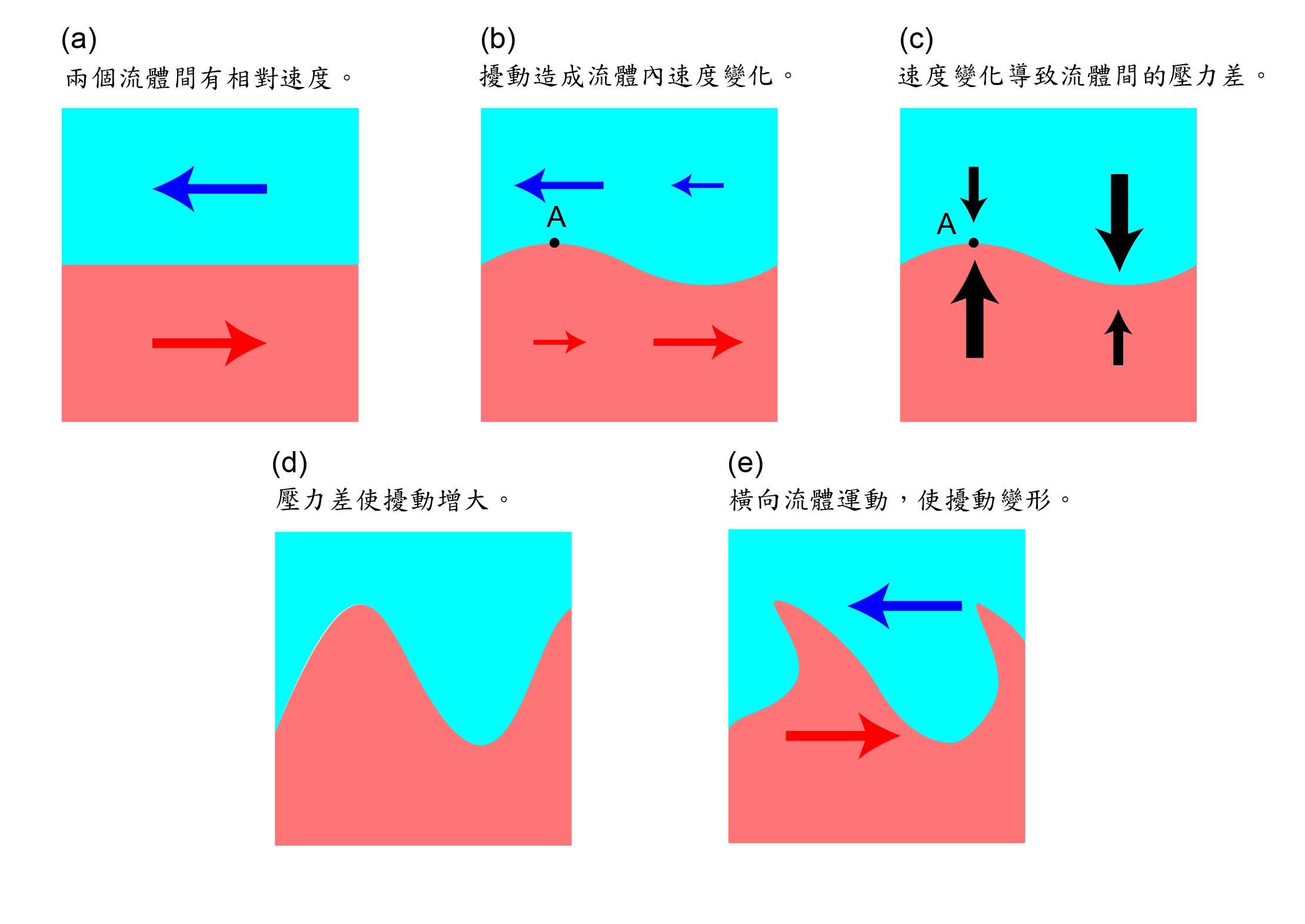
但對於從觀測數據到預測未來而言,「差之毫釐,失之千里」或許是最氣象預報而言簡單而貼切的說法。或許子彈剛發射出去僅僅差不到1 mm的誤差,到了數百公尺外,就會放大到數十倍以上的誤差,對於所謂的一週預報來說,七天後的預報,不準其實是正常的。
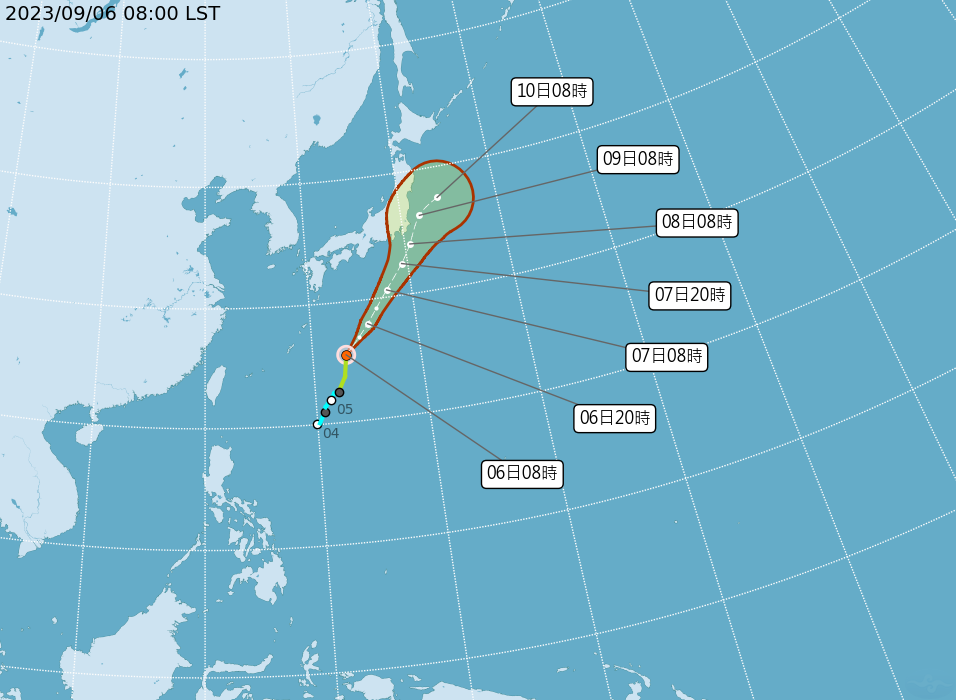
舉個例子,2015 年國研院颱洪中心也發布了下方這張圖,說明模式預報的不確定性,同一颱風會有可能會導致截然不同的路徑結果。圖中三角形點是指 8/21 的颱風位置,編號 1 為 8/11 日的預測結果、2 為 8/12 的結果……以此類推,所以 10 天內的預測,每天都修正超多,代表著超級不確定性。
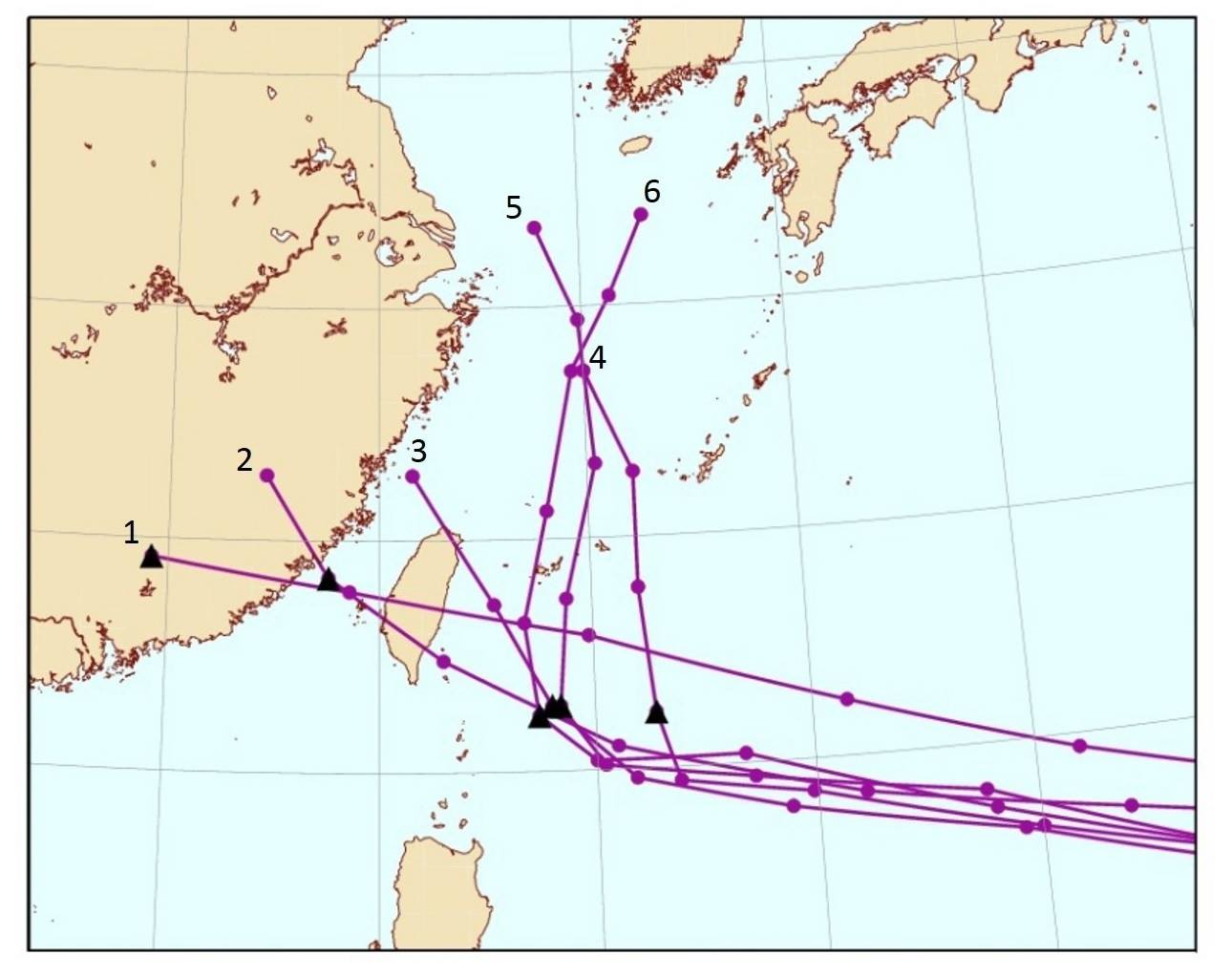
「氣象存在著渾沌(Chaos)的特性」是一個必須要強力宣導的概念,因為在勞侖茲發現大氣渾沌特性之前,大家都認為我們靠著學理和統計,就可以很準確的預測天氣,只要電腦運算速度提升,人人都能成為氣象專家;只是實際上就連千分之一的誤差,都會讓計算結果截然不同。附帶一個複擺的實驗,它是很容易說明渾沌現象的實驗,即使初始值十分接近,但只要有一絲絲誤差就會讓結果差很遠,
既然無法完全準,那幹嘛預測?幹嘛花錢買超級電腦?
那「為什麼只有百分之百準確度才有意義呢?」我們來看看103年國中會考的第一題:
這題降雨機率,根據政府資料開放平台的數據,這題有 8 成 6 答對率,是整本答對人數最多的一題。基本上你看到降雨機率 30% 和 70% 時會做的防雨準備就該不一樣了,甚至取決於你要求做什麼事能接受的「風險」,譬如假如有30%會下雨,雖然機率不高但仍可能降雨,活動能辦是能辦,但沒必要不做雨備跟老天賭不是嗎?
接下來我們談這類的「降雨機率」或是「數值預報」是怎麼來的,它包括統計(就是過去相同數據和天氣模式下有沒有降雨的紀錄)、分析(利用更多數據去建構未來天氣變化可能性的模擬)、研判(專業人員從學理上來判斷)的綜合結果。
超級電腦的用途就是在統計與分析時,能處理更多數據的能力。超級電腦只能讓我們運算時能以更複雜、細微的模型去了解未來的不同可能性,讓我們的預測盡可能的「接近」真實結果,然而再怎麼樣都只是「接近值」,由於大氣的渾沌特性,要做到百分之百的預測是完全不可能的。
但「盡可能的縮小誤差」、「盡可能的提供信賴度高」的預報,一直都是各氣象單位的目的,《祛除氣象預報的迷思》一文就在強調這點,速度快 100 倍的電腦並不會準 100 倍,而是讓我們會有更多可以互相佐證的數據。當然電腦快有好處,只是很難量化,也很難說清楚而已。
為什麼日本美國都會預測的比較準?因為錢多還是科技高嗎?
錢多是事實,台灣颱風論壇的賴重祐先生就撰文比較過台日的氣象預算差異,或許從預算除以國土面積會覺得台灣拿這樣的錢應該也要做出一樣或更好的水準,但我必須要說,可能我們需要預報的國土面積小,但大氣可不是像一堵牆一樣有邊界的,你跨出島外或是幾海浬外就一定不受島內天氣影響嗎?沒人敢說,在進行長期預報時,必須針對大範圍尺度的大氣運動進行計算分析,要算台灣未來一週的天氣也需要中國大陸、日本的資料,需要更大範圍的衛星雲圖,難度可不會因為你只要預報台灣就少很多,這時再來看預算和擁有衛星數量,還會覺得氣象局錢領多不做事我也沒辦法說什麼了…
所以氣象局報不準就可以裝死嗎?氣象法是要讓氣象預報變一言堂?
這也是我常看到的問題,報不準當然不能裝死,但就像我前面提到的,「如何定義什麼叫報不準」其實沒有具體的說法,而在天氣多變的情況下,你要氣象局「統計自己的預報失準率」,無疑是要斷死自己的後路,因為不準的原因可能有:
- 某些季節如春季,氣候多變化本來就超難預測。
- 特殊很少發生的極端氣候事件。
- 預報員經驗不足。
- 對於數據解讀太過保守(高估災害事件、低估一般事件)。
- 其它人為失誤。
問題就在於要把上述原因整合統計資料,如果把原因歸納在前兩項,要怎麼說服立委諸公、一般大眾,在不懂的人看來你用前兩個當結論就是在黑箱啊!然後我們又能容許多少極限的失誤,以目前公務體系的規範下,要執行這樣的天氣預報成效統計,只會讓更多研究或預報人員花更多時間寫報告而不做自己該做的專業事情。
我的看法是,最好還是多加宣導某些天氣情況難以預測、逐時預報的好處,或是逐步引入國外加上「信賴度」表示的方式說明預報的結果誤差範圍。像是要告訴大家春季多變化就可以利用不同季節預報準確度的數據給民眾參考,這樣會比較有實質意義。以日本氣象廳而言,就經常能看到以下的情況,一週預報信賴度由 A~C 等級,即使是七天後的日子,如果是 A 等級的準確率,就可以把那個結果當成是前一天的預報也無妨,如果是 C 等級,那代表著就是還有一定的誤差存在。如果有這樣的資訊,或許就能告訴大家,其實要在這天考量天氣情況時要特別注意不確定性的風險,當然,要落實這樣的預報也要有一定程度的宣導才有效果。

至於氣象法,蠻常聽到有人靠邀說這個是只準州官放火的法令。但在104年有修正過放寬法令,讓民間單位(如天氣風險管理公司)也有適度預報的權限,只是需要「獲得許可」與「證照」,在台灣像是天氣風險與管理公司就有許多取得證照許可的預報人員,我想氣象法的用意並不是讓氣象預報變成一言堂,只是希望預報氣象這件事能夠回歸專業,並避免過度詮釋氣象預報資訊造成民眾恐慌,要是希望一言堂的話那也不會再修法調整了。當然氣象法還有一些執行上可能會出現的 bug,但這不在本文想討論的範圍,就暫時先跳過了。
至於國外的預報呢?氣象法當然管不到那個地方,只是你要是硬要把國外預報的結果拿來跟國內的比,還要比較準度,似乎有點立足點不公平。外國單位預報台灣的氣象是給他們自己看的,用的資料也不會比我們多,計算的模式也不同,是要怎麼比?
談完氣象預報的部分,再來談談媒體角色
從科學傳播的角度來看,氣象預報與民眾的距離就是一種典型的「資訊不對稱」,除了預報結果的資訊,也包括了背景知識的資訊。有些科學記者可以理解氣象預報的極限以及預報結果的不確定性,但也有許多是站在以為自己理解,卻是一知半解的角度看這件事,甚至我也有看到「既然是公務機關,報準,應該;不準,納稅義務人抱怨很正常。」言論,很正常不代表很合理,因為本來就沒有百分百準。媒體引用網路上的資訊與留言報導,看似在發揮監督政府的力量,但卻在背景知識不足的情況下對政府先提出質疑,其實除非從教育大眾的角度出發,否則還真難回答啊!
而另外也聽到一些聲音,認為官僚與機關文化導致預報員會過度保守而忽視科學結果,我覺得僅僅對了一半。為什麼?因為人家要對上級負責、對立院負責的情況下,實務經驗的確會佔很大比重,若要檢討這件事,我想就要先分清楚當預測失準時發生時,原因會有天然與人為因素,但實務上要怎麼分?既然非專業人士無法畫分,那是不是需要專家來協助?直接說誰打臉誰這樣真的恰當嗎?真的有盡到彌平民眾和政府資訊不對稱的落差嗎?從這個角度回來看氣象法,也不難理解至今為何無法完全開放氣象預報了,因為只選擇性的懂一部分,比完全不理解還可怕啊!
沒有說氣象局不用改進,改進是必要的,只是對於氣象預報的誤解,無知的一方也需要主動了解、擁有資訊的一方(氣象局)也該要有更積極的科普宣導。像是最簡單的「晴時多雲偶陣雨」,民眾會問到底是晴、多雲還是雨?但實際上應該是「大多時候應該是晴天,但因為水氣多有時會多雲,偶爾會突然下短暫的雨,會外出朋友還是要帶個雨具以防萬一!」這樣調整說法,不是稍微清楚一點了嗎?誰可以做?氣象局和播報氣象的媒體皆可!
結語:我自己怎麼利用氣象資訊的?
看不同的氣象預報結果,了解不同的分析來評估風險,原意是一件好事,只是拿這種東西的比較作為新聞,會有一種「沒事聊,只好聊天氣」的感覺。多半時間在早上出門前才會看氣象預報,接著再考量今天的衣著,可能看手機內建也可能看氣象局的資訊,原因是我認為越接近的時間,準確度會稍微提升;有時不確定也會看看窗外的天氣,某段時間真的很怕遇到突然的強降雨,就會去找雷達回波圖來看……雖然不是每個人都能解讀一般氣象預報以外更深入的資訊,但或許也可以試著重新思考看看,在沒有百分百完美,但多數時仍準確的預報資訊下,如何運用 & 使用氣象預報資訊,才是對自己最有幫助的?
想知道更多關於地球大小事,可來參觀作者的部落格:地球故事書
- [註1]關於氣象預報的科普文章:
- 《祛除氣象預報的迷思》(此篇原為投稿蘋果)
- 《台北會下雪嗎?為何國內外的天氣預報眾說紛紜?》《為什麼氣象預報老是不準》、《明天會出太陽嗎》(泛科學)
- 《氣象預報為什麼會不準? 》(科學人雜誌)