本文轉載自 Liou YanTing 臉書【相關、因果,傻傻分不清楚】
文/劉彥廷
你一定曾經在網路上看過類似像這樣的研究:
- 「婚禮花費越高,離婚率越高」
- 「家中藏書越豐富,小朋友越聰明」
- 「性生活越活躍的人,越少生病,身體越健康」
- 「抽雪茄的人更長壽」
不曉得你看到這些訊息時,第一反應會是什麼?
是嘴角上揚,莞爾而笑;還是點點頭,對結論表示贊同;又或者是眉頭緊蹙,心想:「嗯……好像哪裡怪怪的。」面對這些試圖告訴你「兩個事件關聯性」的資訊,有思辨習慣的人,會如何思考、解讀它們呢?
今天,就來和你分享一下,要正確理解這些訊息,得先有個概念,叫做——「相關,並不等於因果」。

冰淇淋銷售量與溺死人數
重要的事多說一遍:「相關,不等於因果。」
舉個經典的案例,「研究發現,冰淇淋銷售量越高,溺水死亡人數越多」,也就是「冰淇淋銷量」和「溺死人數」這兩個事件,或者說變數——呈現了「高度正相關」。
相信看到這樣的訊息,任何心智能力正常的人,都不會下結論說:冰淇淋「造成」了溺水。因為所有人都知道,「冰淇淋銷量」與「溺死人數」雖然有相關,但它們並沒有因果關係。
那問題就來了,「為什麼沒有因果關係的兩個事件,彼此會有相關呢?」
聰明的你,一定已經想到了。在這個例子的背後,藏著另一個變因,叫做——「季節」。在夏天,冰淇淋賣得好,銷售量高;同時,在夏天,去玩水的人比較多,意外溺水身亡的人也比較多。這兩個「獨立的事件」,同時並列在一起,就讓「冰淇淋銷量」和「溺死人數」有了相關性。
一旦我們將「季節」這個變因排除,用科學語言來說,叫做「控制住」——兩個事件的相關性就消失了。
表面上相關的史丹佛棉花糖實驗
在日常生活中,有些事件的相關性很單純,就像冰淇淋與溺水的例子,不會讓人誤判,讓人真的以為它們有因果關係。但有很多例子,就沒這麼容易判斷了,甚至,連受過專業訓練的科學家也會誤判。例如你可能聽過的經典實驗——「史丹佛棉花糖」實驗。
史丹佛大學的研究人員找了一群孩子,讓他們單獨待在房間中,並在面前放置一顆棉花糖,接著告訴他們:「如果你能堅持 15 分鐘,不把這顆棉花糖吃掉,你就能得到兩顆棉花糖。」
之後,研究人員對這些孩子們進行了多年的追蹤,並得出一個結論:「那些沒有在一開始吃掉棉花糖的小朋友,也就是擁有『延遲滿足能力』的小朋友,有更好的人生表現。」
這個實驗的結論以及它帶來的啟發,對兒童教育有著極大的影響。許多家長、老師都不約而同的,開始強調要訓練、培養孩子的「延遲滿足能力」。你在博客來搜尋「棉花糖」這幾個關鍵字,也能查到一堆親子教養的書籍。
但你知道嗎?這個實驗結論已經被證明是有問題的了!
後來有研究團隊又重複做了實驗,但這次,他們特別將「家庭背景」這項因素控制起來,結果發現,「延遲滿足能力」與「未來成就」的相關性就不見了。
什麼意思呢?翻譯成白話文就是:決定小朋友未來成就的主要因素,並不是什麼延遲滿足的能力,而是你家裡有沒有錢啊!
那些家裡有錢的小朋友,對他們來說,平常有太多機會可以吃到好吃的糖果、零食,當然實驗時,更容易忍住不吃棉花糖;而家裡越有錢,將來越有機會取得成功,這不是很理所當然的事情嗎?
你看,連這麼有名的實驗,都會犯「相關不等於因果」的錯誤。那我們應該如何正確地看待,這些「表面上有相關」的兩個事件呢?
有相關的五種可能性
當我們說 A 和 B 有相關時,從邏輯的角度來看,有五種可能,接下來我們會依序來舉例說明一下。
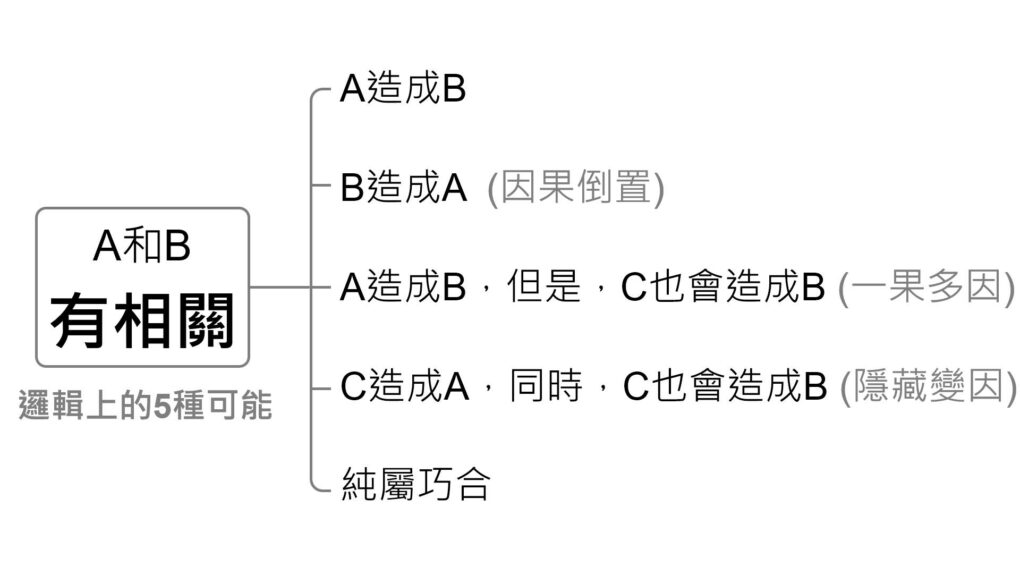
相關不是因果,是 A 造成 B,還是 B 造成 A?
舉個例子,研究發現「性生活越活躍的人,越少生病,身體越健康」。
這則訊息最直觀的解讀也許是,「性生活會讓人更健康」,這叫 A 造成了 B。但有沒有可能反過來是 B 造成了 A 呢?也就是──不是性生活讓人健康,而是越健康的人,才可能有活躍、高頻率的性生活啊!
這樣的思考、解讀,是不是也是一種可能,而且更合理呢?
並非是完整的原因,A 造成 B,但 C 也會造成 B
這種情況簡單來說,就是「一果多因」。我們在現實世界遇到的許多問題,都屬於這一類型。
舉個例子,如果想要證明「死刑具有嚇阻力」,你覺得,需要什麼樣的數據或資料呢?以下是兩種常見的答案:
- 第一種,上網找已經廢除死刑的國家,比較這個國家在廢除死刑前後,犯罪率的變化。如果在廢除死刑後,犯罪率有顯著的上升,那麼就證明了——「死刑的確具有嚇阻力」。
- 第二種,上網找找看,有沒有「曾經」廢除死刑,但之後又恢復死刑的國家,比較這個國家在恢復死刑前後,犯罪率的變化。如果在恢復死刑後,犯罪率有顯著的下降,那麼就證明了——「死刑的確具有嚇阻力」。
這兩種答案,雖然切入的角度不一樣,但背後的思考邏輯都相同,都是試圖以死刑和犯罪率的「因果關係」,來證明死刑具有嚇阻力。
但如果我們再多想一層,這兩組數據,真的可以證明「死刑和犯罪率具有因果關係」嗎?要知道,犯罪是一個複雜的社會問題,影響犯罪率高低的原因有很多,而有沒有死刑,只是眾多原因之一,並不是唯一。
所以,以第一組數據來說,一個國家在廢除死刑後,犯罪率上升。除了廢死這個原因,導致了犯罪率上升外,還有沒有可能有其他原因?比如說,在廢除死刑時,剛好遇到了金融海嘯,或是某個重大災難,導致社會動盪不安、失業率上升,犯罪率也連帶跟著上升。
同樣道理,對於第二組數據來說,一個國家在恢復死刑後,犯罪率下降。除了死刑導致犯罪率下降這種解釋外,有沒有一種可能是,犯罪率下降的原因,是因為這個國家基礎教育做得好、人民素質足夠高,即便沒有死刑,犯罪率也會下降。
在沒有「排除」、「控制」影響犯罪率的「其他變因」之前,如何保證犯罪率的上升或下降,真的是因為死刑存廢所造成的呢?
C 造成 A,同時,C 也會造成 B
前面提到的「冰淇淋與溺水」、「棉花糖實驗」都是這樣的例子,也就是存在一個「隱藏變因」C,同時影響了 A 和 B,以下我再提幾個例子:
- 像是「家中藏書越豐富,小朋友越聰明」,你覺得是大量的藏書,讓孩子變得更聰明了,還是有其他隱藏變因,會讓家中藏書更豐富,同時,也會讓小朋友更聰明呢?
- 又或者是「哈佛畢業生薪水比它校畢業生高」,你覺得是念哈佛,會讓你薪水更高,還是有其他隱藏變因,會讓你容易申請上哈佛,同時,也容易拿到較高的薪水呢?
聰明的你,一定能想到答案。
偽相關,又稱「純屬巧合」
這種純屬巧合的相關,也被稱為「偽相關」。美國有個網站,就蒐集了許多偽相關的數據案例,其中有不少讓人哭笑不得的例子。
例如:「影星尼可拉斯凱吉拍過的電影」和「游泳池溺死人數」,呈現高度正相關;「美國小姐的年齡」和「因取暖設備喪命的人數」,也呈現高度正相關。
看到「有關聯性」,先別急著下定論
行文至此,也寫了快 3000 字。
感謝你願意看完這篇文章,在注意力稀缺的時代,要在社群媒體上看完一篇 3000 字的文章,實屬不易;希望你的大腦還承受得住,沒有當機。
最後總結整理一下,以後若看到一則訊息,試圖告訴你「兩個事件的關聯性」時,在接受它之前,不妨試著先在腦中思考這幾個問題:
- 是前者造成了後者,還是,後者造成了前者其實也說得通呢?——就像「性生活和身體健康」的例子。
- 有沒有其他可能的原因,也會造成同樣結果?——就像死刑嚇阻力的例子。
- 有沒有隱藏變因會同時影響兩者?——就像「冰淇淋和溺水」和經典的「棉花糖實驗」的例子。
- 有沒有可能是純屬巧合?





























 ——本文摘自泛科學 2020 年 5 月選書《
——本文摘自泛科學 2020 年 5 月選書《