從什麽時候開始，冬天變得越來越熱——用統計學的「改變點」及「紀錄」探討台北暖冬的異常現象

本文與 研華科技 合作，泛科學企劃執行。

每次 NVIDIA 執行長黃仁勳公開發言，總能牽動整個 AI 產業的神經。然而，我們不妨設想一個更深層的問題——如今的 AI 幾乎都倚賴網路連線，那如果哪天「網路斷了」，會發生什麼事？

想像你正在自駕車打個盹，系統突然警示：「網路連線中斷」，車輛開始偏離路線，而前方竟是萬丈深谷。又或者家庭機器人被駭，開始暴走跳舞，甚至舉起刀具向你走來。

這會是黃仁勳期待的未來嗎？當然不是！也因為如此，「邊緣 AI」成為業界關注重點。不靠雲端，AI 就能在現場即時反應，不只更安全、低延遲，還能讓數據當場變現，不再淪為沉沒成本。

什麼是邊緣 AI ？

邊緣 AI，乍聽之下，好像是「孤單站在角落的人工智慧」，但事實上，它正是我們身邊最可靠、最即時的親密數位夥伴呀。

當前，像是企業、醫院、學校內部的伺服器，個人電腦，甚至手機等裝置，都可以成為「邊緣節點」。當數據在這些邊緣節點進行運算，稱為邊緣運算；而在邊緣節點上運行 AI ，就被稱為邊緣 AI。簡單來說，就是將原本集中在遠端資料中心的運算能力，「搬家」到更靠近數據源頭的地方。

那麼，為什麼需要這樣做？資料放在雲端，集中管理不是更方便嗎？對，就是不好。

第一個不好是物理限制：「延遲」。
即使光速已經非常快，數據從你家旁邊的路口傳到幾千公里外的雲端機房，再把分析結果傳回來，中間還要經過各種網路節點轉來轉去…這樣一來一回，就算只是幾十毫秒的延遲，對於需要「即刻反應」的 AI 應用，比如說工廠裡要精密控制的機械手臂、或者自駕車要判斷路況時，每一毫秒都攸關安全與精度，這點延遲都是無法接受的！這是物理距離與網路架構先天上的限制，無法繞過去。

第二個挑戰，是資訊科學跟工程上的考量：「頻寬」與「成本」。
你可以想像網路頻寬就像水管的粗細。隨著高解析影像與感測器數據不斷來回傳送，湧入的資料數據量就像超級大的水流，一下子就把水管塞爆！要避免流量爆炸，你就要一直擴充水管，也就是擴增頻寬，然而這樣的基礎建設成本是很驚人的。如果能在邊緣就先處理，把重要資訊「濃縮」過後再傳回雲端，是不是就能減輕頻寬負擔，也能節省大量費用呢？

第三個挑戰：系統「可靠性」與「韌性」。
如果所有運算都仰賴遠端的雲端時，一旦網路不穩、甚至斷線，那怎麼辦？很多關鍵應用，像是公共安全監控或是重要設備的預警系統，可不能這樣「看天吃飯」啊！邊緣處理讓系統更獨立，就算暫時斷線，本地的 AI 還是能繼續運作與即時反應，這在工程上是非常重要的考量。

所以你看，邊緣運算不是科學家們沒事找事做，它是順應數據特性和實際應用需求，一個非常合理的科學與工程上的最佳化選擇，是我們想要抓住即時數據價值，非走不可的一條路！

邊緣 AI 的實戰魅力：從工廠到倉儲，再到你的工作桌

知道要把 AI 算力搬到邊緣了，接下來的問題就是─邊緣 AI 究竟強在哪裡呢？它強就強在能夠做到「深度感知（Deep Perception）」！

所謂深度感知，並非僅僅是對數據進行簡單的加加減減，而是透過如深度神經網路這類複雜的 AI 模型，從原始數據裡面，去「理解」出更高層次、更具意義的資訊。

以研華科技為例，旗下已有多項邊緣 AI 的實戰應用。以工業瑕疵檢測為例，利用物件偵測模型，快速將工業產品中的瑕疵挑出來，而且由於 AI 模型可以使用同一套參數去檢測，因此品管上能達到一致性，減少人為疏漏。尤其在高產能工廠中，檢測速度必須快、狠、準。研華這套 AI 系統每分鐘最高可處理 8,000 件產品，替工廠節省大量人力，同時確保品質穩定。這樣的效能來自於一台僅有膠囊咖啡機大小的邊緣設備—IPC-240。

此外，在智慧倉儲場域，研華與威剛合作，研華與威剛聯手合作，在 MIC-732AO 伺服器上搭載輝達的 Nova Orin 開發平台，打造倉儲系統的 AMR（Autonomous Mobile Robot） 自走車。這跟過去在倉儲系統中使用的自動導引車 AGV 技術不一樣，AMR 不需要事先規劃好路線，靠著感測器偵測，就能輕鬆避開障礙物，識別路線，並且將貨物載到指定地點存放。

當然，還有語言模型的應用。例如結合檢索增強生成 ( RAG ) 跟上下文學習 ( in-context learning )，除了可以做備忘錄跟排程規劃以外，還能將實務上碰到的問題記錄下來，等到之後碰到類似的問題時，就能詢問 AI 並得到解答。

你或許會問，那為什麼不直接使用 ChatGPT 就好了？其實，對許多企業來說，內部資料往往具有高度機密性與商業價值，有些場域甚至連手機都禁止員工帶入，自然無法將資料上傳雲端。對於重視資安，又希望運用 AI 提升效率的企業與工廠而言，自行部署大型語言模型（self-hosted LLM）才是理想選擇。而這樣的應用，並不需要龐大的設備。研華的 SKY-602E3 塔式 GPU 伺服器，體積僅如後背包大小，卻能輕鬆支援語言模型的運作，實現高效又安全的 AI 解決方案。

但問題也接著浮現：要在這麼小的設備上跑大型 AI 模型，會不會太吃資源？這正是目前 AI 領域最前沿、最火熱的研究方向之一：如何幫 AI 模型進行「科學瘦身」，又不減智慧。接下來，我們就來看看科學家是怎麼幫 AI 減重的。

語言模型瘦身術之一：量化（Quantization）—用更精簡的數位方式來表示知識

當硬體資源有限，大模型卻越來越龐大，「幫模型減肥」就成了邊緣 AI 的重要課題。這其實跟圖片壓縮有點像：有些畫面細節我們肉眼根本看不出來，刪掉也不影響整體感覺，卻能大幅減少檔案大小。

模型量化的原理也是如此，只不過對象是模型裡面的參數。這些參數原先通常都是以「浮點數」表示，什麼是浮點數？其實就是你我都熟知的小數。舉例來說，圓周率是個無窮不循環小數，唸下去就會是3.141592653…但實際運算時，我們常常用 3.14 或甚至直接用 3，也能得到夠用的結果。降低模型參數中浮點數的精度就是這個意思！ 

然而，量化並不是那麼容易的事情。而且實際上，降低精度多少還是會影響到模型表現的。因此在設計時，工程師會精密調整，確保效能在可接受範圍內，達成「瘦身不減智」的目標。

模型剪枝（Model Pruning）—基於重要性的結構精簡

建立一個 AI 模型，其實就是在搭建一整套類神經網路系統，並訓練類神經元中彼此關聯的參數。然而，在這麼多參數中，總會有一些參數明明佔了一個位置，卻對整體模型沒有貢獻。既然如此，不如果斷將這些「冗餘」移除。

這就像種植作物的時候，總會雜草叢生，但這些雜草並不是我們想要的作物，這時候我們就會動手清理雜草。在語言模型中也會有這樣的雜草存在，而動手去清理這些不需要的連結參數或神經元的技術，就稱為 AI 模型的模型剪枝（Model Pruning）。

模型剪枝的效果，大概能把100變成70這樣的程度，說多也不是太多。雖然這樣的縮減對於提升效率已具幫助，但若我們要的是一個更小幾個數量級的模型，僅靠剪枝仍不足以應對。最後還是需要從源頭著手，採取更治本的方法：一開始就打造一個很小的模型，並讓它去學習大模型的知識。這項技術被稱為「知識蒸餾」，是目前 AI 模型壓縮領域中最具潛力的方法之一。

知識蒸餾（Knowledge Distillation）—讓小模型學習大師的「精髓」

想像一下，一位經驗豐富、見多識廣的老師傅，就是那個龐大而強悍的 AI 模型。現在，他要培養一位年輕學徒—小型 AI 模型。與其只是告訴小型模型正確答案，老師傅 (大模型) 會更直接傳授他做判斷時的「思考過程」跟「眉角」，例如「為什麼我會這樣想？」、「其他選項的可能性有多少？」。這樣一來，小小的學徒模型，用它有限的「腦容量」，也能學到老師傅的「智慧精髓」，表現就能大幅提升！這是一種很高級的訓練技巧，跟遷移學習有關。

舉個例子，當大型語言模型在收到「晚餐：鳳梨」這組輸入時，它下一個會接的詞語跟機率分別為「炒飯：50%，蝦球：30%，披薩：15%，汁：5%」。在知識蒸餾的過程中，它可以把這套機率表一起教給小語言模型，讓小語言模型不必透過自己訓練，也能輕鬆得到這個推理過程。如今，許多高效的小型語言模型正是透過這項技術訓練而成，讓我們得以在資源有限的邊緣設備上，也能部署愈來愈強大的小模型 AI。

但是！即使模型經過了這些科學方法的優化，變得比較「苗條」了，要真正在邊緣環境中處理如潮水般湧現的資料，並且高速、即時、穩定地運作，仍然需要一個夠強的「引擎」來驅動它們。也就是說，要把這些經過科學千錘百鍊、但依然需要大量計算的 AI 模型，真正放到邊緣的現場去發揮作用，就需要一個強大的「硬體平台」來承載。

邊緣 AI 的強心臟：SKY-602E3 的三大關鍵

像研華的 SKY-602E3 塔式 GPU 伺服器，就是扮演「邊緣 AI 引擎」的關鍵角色！那麼，它到底厲害在哪？

一、核心算力
它最多可安裝 4 張雙寬度 GPU 顯示卡。為什麼 GPU 這麼重要？因為 GPU 的設計，天生就擅長做「平行計算」，這正好就是 AI 模型裡面那種海量數學運算最需要的！

你想想看，那麼多數據要同時處理，就像要請一大堆人同時算數學一樣，GPU 就是那個最有效率的工具人！而且，有多張 GPU，代表可以同時跑更多不同的 AI 任務，或者處理更大流量的數據。這是確保那些科學研究成果，在邊緣能真正「跑起來」、「跑得快」、而且「能同時做更多事」的物理基礎！

二、工程適應性——塔式設計。
邊緣環境通常不是那種恆溫恆濕的標準機房，有時是在工廠角落、辦公室一隅、或某個研究實驗室。這種塔式的機箱設計，體積相對緊湊，散熱空間也比較好（這對高功耗的 GPU 很重要！），部署起來比傳統機架式伺服器更有彈性。這就是把高性能計算，進行「工程化」，讓它能適應台灣多樣化的邊緣應用場景。

三、可靠性
SKY-602E3 用的是伺服器等級的主機板、ECC 糾錯記憶體、還有備援電源供應器等等。這些聽起來很硬的規格，背後代表的是嚴謹的工程可靠性設計。畢竟在邊緣現場，系統穩定壓倒一切！你總不希望 AI 分析跑到一半就掛掉吧？這些設計確保了部署在現場的 AI 系統，能夠長時間、穩定地運作，把實驗室裡的科學成果，可靠地轉化成實際的應用價值。

台灣製造 × 在地智慧：打造專屬的邊緣 AI 解決方案

研華科技攜手八維智能，能幫助企業或機構提供客製化的AI解決方案。他們的技術能力涵蓋了自然語言處理、電腦視覺、預測性大數據分析、全端軟體開發與部署，及AI軟硬體整合。

無論是大小型語言模型的微調、工業瑕疵檢測的模型訓練、大數據分析，還是其他 AI 相關的服務，都能交給研華與八維智能來協助完成。他們甚至提供 GPU 與伺服器的租借服務，讓企業在啟動 AI 專案前，大幅降低前期投入門檻，靈活又實用。

台灣有著獨特的產業結構，從精密製造、城市交通管理，到因應高齡化社會的智慧醫療與公共安全，都是邊緣 AI 的理想應用場域。更重要的是，這些情境中許多關鍵資訊都具有高度的「時效性」。像是產線上的一處異常、道路上的突發狀況、醫療設備的即刻警示，這些都需要分秒必爭的即時回應。

如果我們還需要將數據送上雲端分析、再等待回傳結果，往往已經錯失最佳反應時機。這也是為什麼邊緣 AI，不只是一項技術創新，更是一條把尖端 AI 科學落地、真正發揮產業生產力與社會價值的關鍵路徑。讓數據在生成的那一刻、在事件發生的現場，就能被有效的「理解」與「利用」，是將數據垃圾變成數據黃金的賢者之石！

👉 更多研華Edge AI解決方案
👉 立即申請Server租借

• 本文轉載自林澤民的部落格

「多重宇宙」是我教統計時常用到的名詞，我用它來解釋隨機變異（stochastic variation）的概念：

例如民調抽得一個樣本，此樣本的受訪者固然是一群特定人士，但理論上我們可以抽出許多許多樣本，這些樣本之間雖然會有隨機變異，但樣本彼此的宏觀性質仍會相近。這些不同的隨機樣本，可以以「多重宇宙」一詞來形容。即使事實上只有一個樣本（一個宇宙），我們可以想像在多重宇宙的每個宇宙裡，都有一個微觀上隨機變異的樣本存在。

什麼是隨機樣本？

其實，數理統計學中「隨機樣本」（random sample）的概念指的是「一組獨立且同一分布的隨機變數」（a set of independently and identically distributed random variables）。

在這個定義之下，樣本的每一個單位（資料點）都不是固定不變的數值，而是一個依循某機率分布的隨機變數。「隨機樣本」的要求是樣本所有的 Ｎ 個單位不但要互相獨立，而且要依循同一的機率分布。

我們可以想像我們平常所謂「一個樣本」的 Ｎ 個觀察值，每一個觀察值背後都有一個產生這個數值的隨機變數，也可以說所謂「一個樣本」其實只是這「一組獨立且同一分布的隨機變數」的一個「實現」（realization）。那麼，不同的樣本就是這「一組獨立且同一分布的隨機變數」的不同「實現」。這樣了解之下的不同樣本、不同「實現」，我喜歡把它們稱為「多重宇宙」。

多重宇宙中的隨機變異，是我們在分析一個樣本的資料時必須作統計推論的原因。

比如我們分析本屆所有 113 位立委的議事行為，既然立委一共只有 113 人，我們分析的對象不就是立委的母體嗎？那是不是就不必做統計推論？

不是！原因是我們仍然可以想像有多重宇宙存在，每個宇宙都有 113 位立委，而同一位立委在不同的宇宙裡其議事行為會有隨機變異。正是因為這隨機變異的緣故，我們即使分析的是所謂「母體」，我們仍然要做統計推論。

「多重宇宙」的概念可以說就是「假如我們可以重來」的反事實思想實驗。被分析的單位不是在時間中重來一次，而是在多重宇宙的空間中展現「假如我們可以重來」的隨機變異的可能性。

名為 Monday 的這集 X 檔案電視劇中，主角的夢境不斷重複，每次夢境的結構大致類似，但細節卻有所不同，這正是「多重宇宙—隨機變異」概念的戲劇化。

【媽的多重宇宙】（Everything Everywhere All at Once）也是。

「看，這是你的宇宙，一個漂浮在存在宇宙泡沫中的泡泡。周圍的每個氣泡都有細微的變化。但你離你的宇宙越遠，差異就越大。」——【媽的多重宇宙】對白

這是說：變異程度越小的是離你越近的宇宙，程度越大的是離你越遠的宇宙。這裡所謂變異的程度，在統計學裡可以用誤差機率分布的標準差來衡量。

什麼是隨機變異？

關於「隨機變異」這個概念，我最喜歡的例子是研究所入學申請的評審。

例如有 120 人申請入學，我詳細閱讀每人投遞的申請資料（包括性別、年齡等個人特質還有 SOP、大學成績單、GRE 分數、推薦信等），然後打一個 Y=0～100 的分數。全部評閱完畢，我便得到一份 N=120 的資料。這個資料包括了所有的申請者，那麼它是樣本呢？還是母體？

如果我要分析我自己評分的決定因素，我會把分數 Y 回歸到性別、年齡等個人特質以及資料中可以量化的變數，例如大學成績平均分數（GPA）和 GRE 分數。跑這個迴歸時，需不需要做統計推論，看迴歸係數是不是有統計的顯著性？

我的看法是這份 N=120 的資料是樣本而不是母體，做迴歸分析當然要做統計推論。

那麼我資料的母體是什麼？

迴歸分析資料的母體其實是所謂「母體迴歸函數」（population regression function），也就是通常所說的「資料產生過程」（data generating process, DGP）。

這個 DGP 就是我在評閱每份資料時腦海中的思考機制，它考量了許多量化和質化的變數，賦予不同的權重，然後加總起來產生 Y。

量化變數的權重就是母體迴歸函數的係數，質化變數則是母體迴歸函數的係數的誤差項。如果有很多質化變數攏總納入誤差項，我們通常可以根據中央極限定理，假設誤差項是呈現常態分布的隨機變數。這個誤差項就是「隨機變異」的來源。

評審入學申請，我通常只把所有資料評閱一次。這一次評審結果，會有幾家歡樂幾家愁，這便構成了一個「宇宙」。如果我第二天又把所有 120 份資料重新評分一遍，得到第二個樣本。因為我腦中的「資料產生過程」包括隨機變數，這個新樣本保證跟第一個樣本會有差異。用白話說：我的評分機制不精確，我自己甚至不知道我給每個量化變數多少權重，而且第二次評閱所用的權重也會跟第一次不盡相同，更不用說質化變數如何影響我的評分了。

這第二個樣本，申請者的排比不會跟第一個樣本一樣，雖然也是幾家歡樂幾家愁，歡樂與愁悶的人也可能不一樣。這是第二個宇宙。依此類推，我們可以想像同樣的120位申請者，因為我「資料產生過程」的隨機變異，活在多重宇宙裡。

這些宇宙有的差異不大，根據【媽的多重宇宙】的說法，它們的泡泡互相之間的距離就較近，差異較大的宇宙，距離就較遠。如果申請者可以像電影所述那樣做宇宙跳躍，他們會看到自己在不同宇宙裡的命運。

我擔任德州大學政府系的研究部主任時，常耽心有申請者拿我們入學評審委員的評分資料去做迴歸分析。如果分析結果顯示種族、性別等變數有統計顯著性，說不定會被拿去控告我違反所謂「平權行動」（affirmative action）的相關法律。如果沒有顯著性，我就不耽心了。

多重宇宙之間會不會有「蝴蝶效應」？也就是宇宙跳躍時，隨機變異產生的微小差異，會不會造成新舊宇宙生命路徑的決然不同？

在【媽的多重宇宙】中，伊芙琳只要當初做了一個不同的決定，以後的生命便可能跟現世（home universe）有很不一樣的命運。這在統計學也不是不可能。時間序列分析中，有些非線性模式只要初始值稍微改變，其後在時間中的路徑便會與原來的路徑發散開來。

你做時間序列分析時，會不會想想：時間序列資料究竟是樣本還是母體？如果你的研究興趣就只限於資料期間，那要不要做統計推論？當然要的，因為隨機變異的緣故。

如果你今年申請外國研究所不順利，也許在另一個宇宙裡，你不但獲名校錄取，得到鉅額獎學金，而且你的人生旅途將自此一路順遂，事業婚姻兩得意呢。

台灣這幾天比較冷，但暖冬仍然是全球暖化過程中一個明顯的趨勢。一般以為全球暖化始於 19 世紀末葉先進國家積極工業化的時候，但世界各地工業化的進程不同，暖化的趨勢也會有所差異。當工業化在全球範圍內日益普及，各地暖化趨勢便益見明顯，但還要等到 20 世紀下半葉這趨勢才明顯到引起各國的注意。

在美國，一直要到 1988 年氣候變化才正式成為官方關切的議題。這一年的 6 月 23 日，NASA 太空研究所（GISS）主任 James E. Hansen 在參議院能源及自然資源委員會作證指出：「全球暖化的程度已經顯著到讓我們確信溫室效應與暖化趨勢具有因果關係。依我的意見，我們已經偵測出了溫室效應，而且這效應正在影響我們的氣候。」

以筆者居住的德州奧斯汀市而言，氣溫紀錄始於 19 世紀末期。我用統計學「改變點」（change point）的方法分析每年最高溫及最低溫的時間序列，檢測出年低溫最顯著的改變點在 Hansen 作證之後 3 年的 1991 年，而年高溫的改變點還要更後，在 1998 年。這與筆者個人體驗大致相符。

台北氣溫變化趨勢的改變點

「改變點」的檢測是時間序列分析的統計方法，它用來判定時間序列的資料產生過程是否有不連續點的存在。它在 1930 年代就曾被產業界用來監控產品的製造過程，其後經過數學家的深入研究，在近 20 年來蓬勃發展，廣泛被應用於環保、疫情、醫療、軍事、反恐等各領域。筆者個人就曾用類似的研究方法發現美國歷史上，選民的投票行為在二十世紀 20-30 年代之間曾經發生過質性的變化。去年五月，頂級學術期刊 Science 也有研究論文檢測新冠肺炎在德國傳播趨勢的改變點，肯定了政府干預措施的有效性。CBS 電視影集「數字」（Numb3rs）甚至有一集演出「夢幻棒球」玩家用改變點方法檢測大聯盟球員使用禁藥提高打擊率的故事。

台灣的氣溫紀錄也始於 19 世紀末。根據 Jasmine Kuo 提供的台北市年低溫歷史資料，台北市每年最低溫的改變點在 1975 年，而年高溫的改變點則要到 2001 年。台北市年低溫的改變比奧斯汀要早，這也許跟地形、地理位置、人口、以及工業化程度有關。

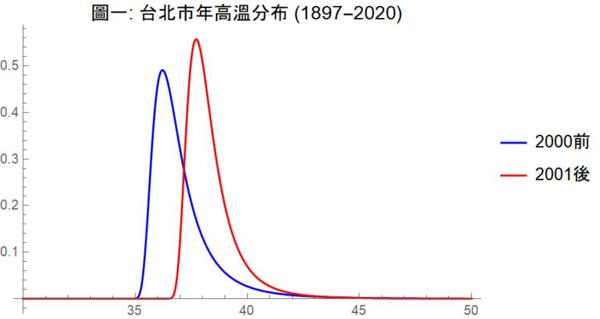
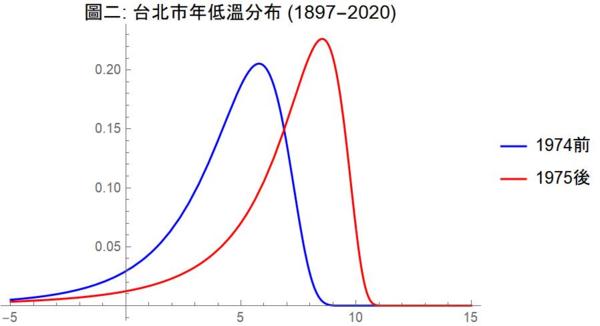
理論上，年高溫及年低溫都不是常態分布，而是呈現所謂極端值分布（extreme value distribution）。圖一及圖二以上述改變點為斷點，分別估計年高溫及年低溫在各自改變點前、後的極端值分布。這兩張圖讓我們清楚看出改變點前後的明顯差異：改變點之後，年高溫及年低溫的分布均明顯往高溫方向移動。年高溫在 2001 之後的平均值增加了攝氏 1.44 度，而年低溫在 1975 之後的平均值則更誇張地增加了將近兩倍的 2.81 度!

時間序列資料產生過程的變化除了可以用改變點的統計方法來檢測斷點以外，也可以用 「紀錄」（record）發生的機率理論來分析異常現象。事實上，事件發生頻率的改變也是改變點研究的數學方法之一。本文以下即以紀錄理論進一步探討台北市年低溫在 1975 年之後新紀錄節節升高的現象。

破紀錄次數的機率分布，説明台北市年低溫變遷出現異常

台北市 1897-2020 年低溫時間序列顯示，1897 年台北市的最低溫是攝氏 5 度。以此為資料中的第一個紀錄，124 年來，有 9 個新的紀錄出現，分別是：1899（7.2度），1905（7.6度），1909（8.1度），1912（8.2度），1976（8.5度），1983（9.3度），1988（10度），2017（10.4度），2019（11.6度）。見圖三時間序列中的黑點。

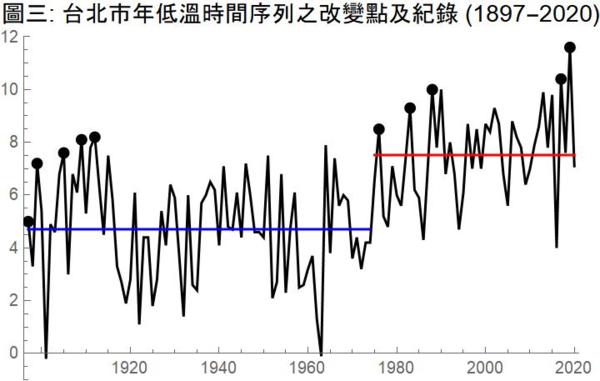
124 年間有 10 個紀錄是正常現象嗎？這個問題，可以用機率理論做精確的回答。

機率理論對「記錄」的研究有很完整的系統。其數學繁複，但相當有趣，有興趣的讀者可以找相關書籍來看，例如 Jiri Andel（2001）的 Mathematics of Chance。

這個理論從一個前提出發：觀察序列中的資料是遵循相同機率分布而且相互獨立（iid，編按：Independently and identically distributed）的隨機變數。在這個假設之下，我們可以導出在 n 個資料點中有 r 個紀錄（包括第一個資料點）的機率分布。這個前提可以說是「正常」狀況的「虛無假設」：它代表觀察序列中資料的產生過程完全相同，沒有任何異常現象或動態趨勢。如果我們的經驗資料與這個假設之下的機率分布不相諧，根據傳統次數主義（frequentist）統計推論的方法，我們可以在一定的統計水平之下拒絕虛無假設而判定異常現象的存在。

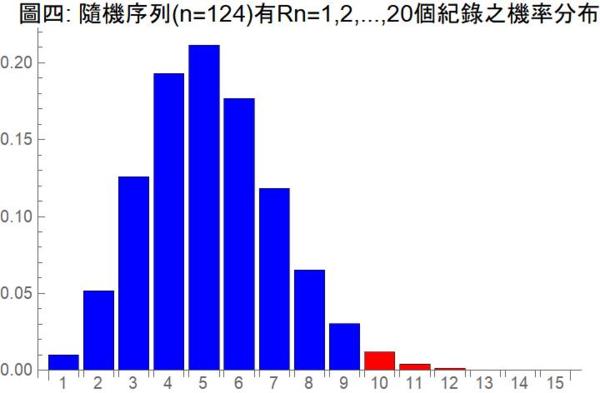
以台北市年低溫的歷史資料來說，我們可以算出在 n = 124 個觀察值的序列資料中出現 r （r = 1，2，3，…，124）個紀錄的機率分布，然後從這分布算出 r 大於或等於 10 的右尾機率。如果這個機率小於相約成俗的顯著水平 0.05，我們判定歷史資料與虛無假設不相諧，從而排除台北市年低溫變遷沒有異常現象的前提。依照傳統統計推論，我們可以做出台北市年低溫變遷有異常現象的結論。

以 Rn 代表在 iid 假設之下，n = 124 個序列資料中有 r 個紀錄的隨機變數，圖四便是 Rn = r 的機率分布。從這個機率分布我們可以算得 Rn 的期望值是 E ( Rn ) = 5.40，變異量是 Var ( Rn ) = 3.76，也很容易直接算得右尾機率 P (Rn ≥ 10) = 0.025。因為這個機率小於 0.05，單尾檢定讓我們得到台北市年低溫屢破歷史上限紀錄是異常現象的結論。（如果一定要用雙尾檢定，這個結論就有點勉強。）

Rn 的機率分布並不容易算，有一個遞歸公式，當 n 較大時，需要很大的計算能量或很久的時間才算得出。要迅速算出，必須用到所謂「第一類史特靈數」（Stirling Numbers of the First Kind）。如果你的軟體沒有這個函數，可以利用這兩個很漂亮的公式來算 Rn 的期望值和變異量：

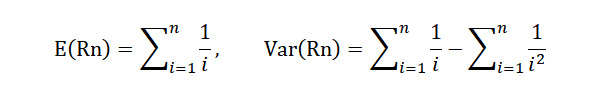
利用這兩個公式也可算出當 n = 124 時，E ( Rn ) = 5.40，Var ( Rn ) = 3.76。如果我們假設 Rn 的分布是常態分佈，則可以輕易算出以以期望值為中心的 95% 信心區間為（1.49，8.88）。因為經驗值 10 個紀錄在信心區間之外，這個分析也支持台北市年低溫變化異常的結論。不過因為 Rn 的分布並非常態，這個分析並不精確。

新紀錄等待時間的機率急遽下降

應用紀錄之機率理來分析台北市氣溫變化也可以看出 1975 年前後是一個轉捩點。

在 1897 年之後的 9 個新紀錄當中，出現在 1975 年之後短短 45 年之間的就有 5個，平均每 9 年就有一個新紀錄。而在 1976 年前的 80 年中，則平均要將近 16 年才有新的紀錄。事實上，1912 年的紀錄保持了 64 年才被打破。

也許你會說 1897-1912，在短短 16 年之間不是就有 4 個新紀錄嗎？然而新紀錄的頻率在紀錄開始之時本來就會比較頻繁，日久後要破紀錄會越來越難。紀錄的機率理論可以算在一定時間之內舊紀錄會被打破的機率，其公式如下：

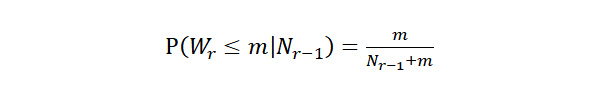
這公式所求的是在第 r – 1 個紀錄發生之後，下一個紀錄的等待時間小於或等於 m 之機率。表一之第六行顯示：從第一個紀錄發生在 1897 年開始，第二個紀錄等待了兩年就發生了，按照上式，第二個紀錄在 2 年之內發生的機率為 0.67。第二個紀錄發生在 1899 年之後，第三個紀錄等待了 6 年發生，而其在 6 年之內發生的機率也是 0.67。第三個紀錄發生在 1905 年之後，第四個紀錄要等待 13 年才發生，而其在 13 年之內發生的機率是 0.31。依此類推。這些機率都不小，雖然紀錄頻頻被打破，並不令人意外。尤其是第五個紀錄發生在 1912 年之後，第六個紀錄要等 64 年才在 1976 年發生，因為等了夠久了，其在這一段期間發生的機率是很高的（0.80）。

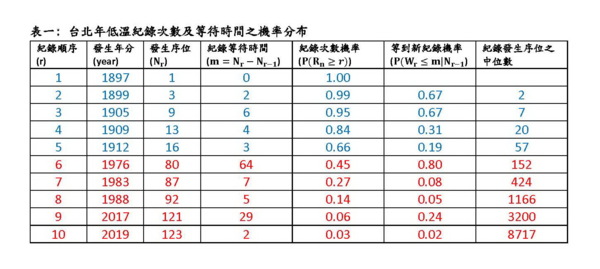
但從 1976 年以後，這個等到下一個紀錄的機率就急遽下降了。第七個紀錄在 7 年內發生，其機率是 0.08；第八個紀錄在 5 年內發生，其機率是 0.08；第九個紀錄等了 29 年，其機率稍大，但它發生之後，第十個紀錄只等了 2 年就發生，其機率小於 0.03。這樣的小機率事件發生了，如果還說氣候沒有異常，在統計學理上是無法接受的。如果我們換一個角度來看，把 1976 年當作氣候質變之後的第一個紀錄，則其後發生在 1983、1988、2017 的新紀錄其等待時間的機率（0.88，0.38，0.69）都不小，不算奇怪。只有 2019 的紀錄還在 0.05 的水平之內，不過這也可以說氣候變化越來越厲害了。

從新紀錄的等待時間來探討氣候變遷還可以看看新紀錄發生的平均時間。不過很奇妙的是：機率理論告訴我們，新紀錄雖然一定會發生（發生的機率為 1），其發生時間的期望值或理論平均數卻是無窮大，即使第二個紀錄也是一樣。以第二個紀錄為例，其發生時間為 2，3，4，…，t，…年的機率分別為 1/2，1/6，1/12，… 1 / t ( t – 1 )，…，所以期望值為 1 + 1/2 + 1/3 + … + 1 / ( t – 1 ) + …。這是有名的無窮和諧數列，它不是收斂數列，其和無窮大。其它的紀錄也是一樣。

不過我們雖然不能算發生時間的期望值，卻能算中位數，也就是發生機率最接近 1/2 的時間點。表一的第七行列出各紀錄發生時間的中位點。我們可以看到，一直到 1976 年的第六個紀錄為止，中位時間點都還算合理。此後，第七個紀錄的中位發生點要在 1897 年算起的第 424 年，第七個紀錄在第 1166 年，第九個紀錄在第 3200 年，第十個紀錄在第 8717 年。這些紀錄的中位發生時間在這麼久遠之後，如果說沒有氣候變化，誰能相信？

附帶一提，1897 – 2020 之間台北市年低溫往下探的紀錄，包括 1897 年的第一個紀錄，124 年之間只有三個：1897（5度），1898（3.3度），1902（-0.2度）。從 1902 年以來，118 年之中，-0.2 度的紀錄沒有被突破！（不過 P ( Rn ≤3 ) = 0.162 並不足以作為氣溫變化異常的統計證據。）

• 本文亦同步刊載於林澤民的部落格，原文標題為〈用「改變點」及「紀錄」探討台北暖冬的異常現象〉

1. 齊斯．德福林（Keith Devlin）、蓋瑞．洛頓（Gary Lorden）著，蘇俊鴻、蘇惠玉等譯。2016。〈改變點偵測：災難即將發生的證據何時開始浮現？〉，《案發現場：FBI警探和數學家的天作之合》（The Numbers behind Numb3rs: Solving Crime with Mathematics）第四章。八旗文化。
2. Jiri Andel, 2001. “Records.” Chapter 4 of Mathematics of Chance. Wiley.
3. 盧孟明、卓盈旻等著。2012。〈台灣氣候變化：1911-2009年資料分析〉。中央氣象局。

• 作者：墨爾 David S. Moore、諾茨 William I. Notz
• 譯者：鄭惟厚、吳欣蓓

實驗法中「隨機化」的必要性

隨機化比較實驗是統計學裡面最重要的概念之一。它的設計是要讓我們能夠得到釐清因果關係的結論。我們先來弄清楚隨機化比較實驗的邏輯：

• 用隨機化的方法將受試者分組，所分出的各組在實施處理之前，應該各方面都類似。
• 之所以用「比較」的設計，是要確保除了實驗上的處理外，其他所有因素都會同樣作用在所有的組身上。
• 因此，反應變數的差異必定是處理的效應所致。

我們用隨機方法選組，以避免人為指派時可能發生的系統性偏差。例如在鐮形血球貧血症的研究中，醫師有可能下意識就把最嚴重的病人指派到羥基脲組，指望這個正在試驗的藥能對他們有幫助。那樣就會使實驗有偏差，不利於羥基脲。

從受試者中取簡單隨機樣本來當作第一組，會使得每個人被選入第一組或第二組的機會相等。我們可以預期兩組在各方面都接近，例如年齡、病情嚴重程度、抽不抽菸等。舉例來說，隨機性通常會使兩組中的吸菸人數差不多，即使我們並不知道哪些受試者吸菸。

新藥研究上不隨機分組帶來的後果：安慰劑效應

如果實驗不採取隨機方式，潛藏變數會有什麼影響呢？安慰劑效應就是潛藏變數，只有受試者接受治療後才會出現。如果實驗組別是在當年不同時間進行治療，所以有些組別是在流感季節治療，有些則不是，那麼潛藏變數就是有些組別暴露在流感的程度較多。

在比較實驗設計中，我們會試著確保這些潛藏變數對全部的組別都有相似的作用。例如為了確保全部的組別都有安慰劑效應，他們會接受相同的治療，全部的組別會在相同的時間接受相同的治療，所以暴露在流感的程度也相同。

要是告訴你，醫學研究者對於隨機化比較實驗接受得很慢，應該不會讓你驚訝，因為許多醫師認為一項新療法對病人是否有用，他們「只要看看」就知道。但事實才不是這樣。有很多醫療方法只經過單軌實驗後就普遍使用，但是後來有人起疑，進行了隨機化比較實驗後，卻發覺其效用充其量不過是安慰劑罷了，這種例子已經不勝枚舉。

曾有人在醫學文獻裡搜尋，經過適當的比較實驗研究過的療法，以及只經過「歷史對照組」實驗的療法。用歷史對照組做的研究不是把新療法的結果和控制組比，而是和過去類似的病人在治療後的效果做比較。結果，納入研究的 56 種療法當中，用歷史對照組來比較時，有 44 種療法顯示出有效。然而在經過使用合適的隨機化比較實驗後，只有 10 種通過安慰劑測試。即使有跟過去的病人比，醫師的判斷仍過於樂觀。

目前來說，法律已有規定，新藥必須用隨機化比較實驗來證明其安全性及有效性。但是對於其他醫療處置，比如手術，就沒有這項規定。上網搜尋「comparisons with historical controls」（以歷史對照組來比較）這個關鍵字，可以找到最近針對曾使用歷史對照組試驗的其他醫療處置，所做的研究。

對於隨機化實驗有一件重要的事必須注意。和隨機樣本一樣，隨機化實驗照樣要受機遇法則的「管轄」。就像抽一個選民的簡單隨機樣本時，有可能運氣不好，抽到的幾乎都是相同政治傾向一樣，隨機指派受試者時，也可能運氣不好，把抽菸的人幾乎全放在同一組。

我們知道，如果抽選很大的隨機樣本，樣本的組成和母體近似的機會就很大。同樣的道理，如果我們用很多受試者，加上利用隨機指派方式分組，也就有可能與實際情況非常吻合。受試者較多，表示實驗處理組的機遇變異會比較小，因此實驗結果的機遇變異也比較小。「用足夠多的受試者」和「同時比較數個處理」以及「隨機化」，同為「統計實驗設計」的基本原則。

——本文摘自《統計，讓數字說話》，2023 年 1 月，天下文化出版，未經同意請勿轉載。