文字

數字會說話，但不一定是真話？別輕易相信統計數據！

活躍星系核・2019/10/18 ・3829字・閱讀時間約 7 分鐘・SR值 545 ・八年級

Brian 北京大學物理學院

不只是學術研究，我們常常會用「統計數據」來作為觀察世界的佐證，但我們在看待數據時要非常小心，因為詮釋方式的不同，其「統計學」所呈現出來的結果，有時候反而可以誤導別人。不信？就讓我們用一些例子，來看看「數據統計」有時不是我們想的那樣。

是數據真的很美，還是只是過擬合？

我們先介紹一個常犯的錯誤：過擬合（overfitting，或稱過適、過度擬合）。過擬合指的是在統計學中調適一個統計模型時，使用過多參數。具體來說，擬合就是把平面上一系列的點，用一條光滑的曲線連接起來。因為這條曲線有無數種可能，從而有各種擬合方法。所以其實你只要有心，任何數據都可以擬合成任何函數。

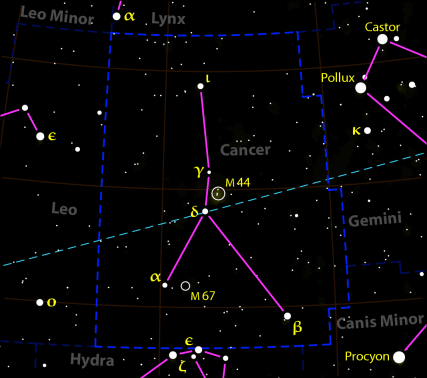
夜空中的星座就是一個很好的例子，明明只看到幾個點，但非要將其擬合成某種動物，看巨蟹座的樣子更像一支叉子或彈弓吧，怎麼會看成螃蟹呢？

再來如果數據量足夠多，你幾乎可以在任何事情間發現相關性，甚至可以說：告訴我你想要什麼結論，都可以給擬合出來。統計學中有個名詞叫做偽相關，指在兩個沒有因果關係的事件，可能基於其他未見的潛在變數，顯示出統計學上的相關，讓人很容易猜想「兩個事件有所聯繫」，然而這種聯繫並不能通過更加精細的檢驗。

諾貝爾獎與巧克力之間的距離？

曾有人在無意間把本國的巧克力消費量和本國諾獎得主佔總人口數的比例進行對比後意外地發現這兩者竟然呈正相關，也就是說越愛吃巧克力的國家諾獎的比例也越高，特別是瑞士人超愛吃巧克力也拿了超多諾獎。

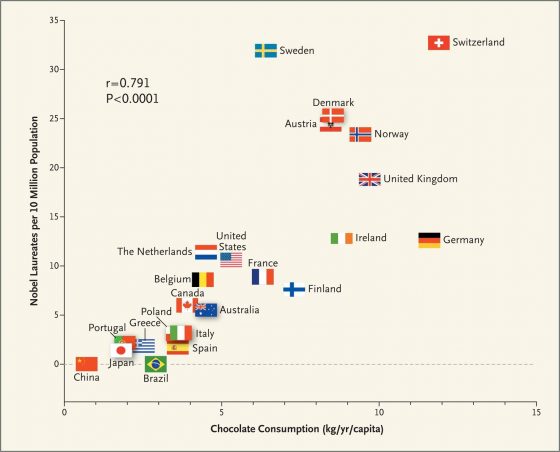
當然我們可以很簡單的理解，由於巧克力消費量與國家的富裕程度相關，而高品質的科研也與國家的富裕程度相關。因此巧克力會與諾獎得主比例相關，但是顯然其中並不存在因果關係。

所以如果你有個命題，而且有數據可以支持此命題，那你要切記，數據和理論吻合的好並不代表你的推論就是對的，「數據吻合的好」只是充分而非必要條件。諾獎和巧克力就是個很好的例子，有時我們會得到很荒謬的結論。

「用四個參數我可以擬合出一頭大象，而用五個參數我可以讓牠的鼻子擺動」

2004 年戴森*在 Nature 雜誌上寫了一篇名為「A meeting with Enrico Fermi」的文章，回憶 1953 年他由理論計算得到了與費米的實驗觀測值十分相符的結果後馬上跑去見費米。當戴森跨進費米的辦公室並遞上自己的計算結果時，費米掃了一眼就把它放下，費米說：「做理論物理學的計算有兩種方式。一種是我喜歡的，就是要對你正在計算的過程擁有一個清晰的物理圖像。另一種是得到精確而且一致的數學形式體系。而這兩者你都不具備。」戴森當時有點驚呆了，但他還是斗膽問費米，為什麼他的理論算不上是一致的數學形式體系。

註解：戴森最著名的成就是證明了施溫格和朝永振一郎發展的變分法方法和費曼的路徑積分表述等價，為量子電動力學的建立做出了決定性的貢獻，這三人在1965年獲得諾獎，學界普遍認為戴森值得拿諾獎，不過戴森還活著，活著就還有希望

費米反問道：「你們在計算過程中引入了多少個任意參數？」戴森回答說四個。於是費米便說：「我記得我的朋友馮·諾依曼曾經說過，用四個參數我可以擬合出一頭大象，而用五個參數我可以讓它的鼻子擺動。」戴森承認，與費米的這次會面是他人生的一個重大轉捩點，50 年後回頭再看，費米是極富遠見的，當年戴森所看好的理論則走到了盡頭。

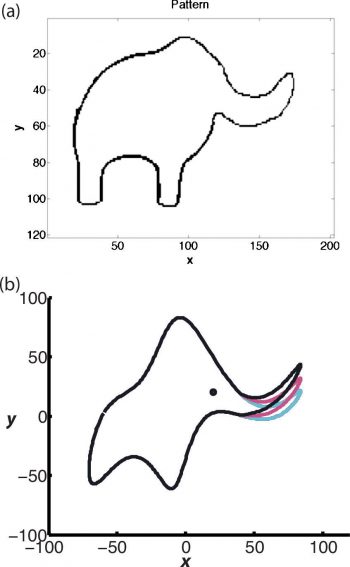
儘管費米本人沒有活到夸克模型問世的那一天，但是他出眾的物理直覺告訴他，戴森等人所採用的含有四個參數的理論一定是錯誤的。費米的一席話及時阻止了戴森和他的團隊走入一個死胡同，從而使他們的興趣轉向更有意義的科學問題。這篇文章還有一個副標題「 How one intuitive physicist rescued a team from fruitless research（一位富有直覺的物理學家如何從死胡同中拯救了一支團隊）」。

只要「仔細」處理數據就可以讓暗物質消失或出現

暗物質的組成成分和其是否存在一直都是物理學界的大問題，去年三月時耶魯大學的 Dokkum 教授宣稱他們發現了一個缺乏暗物質的星系，但這文章一發布就接連跑出一堆文章攻擊他們數據分析太粗糙。因為當在追蹤這麼小的樣品時，速度的不確定度和真正測量的彌散速度是在同一個數量級，所以最終結果就對所使用的技術和處理不確定度的方式極為敏感。

也有人表明說會得到星系缺乏暗物質的結果是因為這些質量估計的不確定度被大大低估了。而且如果把 Dokkum 處理數據的方式套用在一個我們已經充分研究的星系上，會得出這樣的結論：它具有「過大的」暗物質暈，或者它缺少暗物質。你想要得到怎樣的結論取決於你怎麼估計質量，所以才會說只要「仔細」處理數據就可以讓暗物質消失或出現。而且如下圖所示，他們就是直接忽略了一組數據，無視藍圈的那些數據不做擬合。

還有人跑出來狠狠批評 Nature 就喜歡收吸人眼球的文章，而非最符合科學方法的文章。甚至開玩笑說如果同一組數據，用兩種不同的分析數據方式，得到兩個結論，一個是此星系含有暗物質、另一個是此星系缺乏暗物質，那缺乏暗物質的文章更有可能被登出來，因為這能製造大新聞。

對統計學的批評古已有之，已經有不少統計學家指出 p-值使用中存在大量的缺陷，甚至開始轉而質疑用統計學方法計量科學發現。美國國家統計協會（ASA）作爲統計學標準的倡導者給出了一個使用 p-值的參考性聲明。他們認為：「這是科學中最骯臟的秘密：使用統計假設檢驗的「科學方法」建立在一個脆弱的基礎之上。」「假設檢驗中用到的統計方法比臉書隱私條款的缺陷還多。」

科學權威的數據造假

除了統計學本身的問題外，更過分的是還有些科學家會進行數據造假來得到他們想要的結論，歷史上曾有不少知名科學家也做過數據造假的事，以下舉幾個例子：

1919年愛丁頓在西非普林西比島觀測日全食，觀察到引力透鏡現象並以此證實廣義相對論，但後世的科學史家們對於愛丁頓的數據感到懷疑，認為他們肯定做了一些操作來篩選數據。還有密立根做了著名的油滴實驗測量來測量單一電子的電荷，也因而獲得1923年的諾貝爾物理學獎，但後來被踢爆他從 140 次觀測中只採集那些對他有利的漂亮資料，而不利的資料則一概刪去，最後只發表 58 次觀測結果。

道爾頓被認為是歷史上第一個從實驗上證實了化學反應中各個物質總是按照一定的比例進行反應的。這實際上成為物質是由原子或分子組成的間接的證據，在物理、化學乃至整個科學發展史中都具有十分重要的地位。也許有些令人啼笑皆非的是，道爾頓的發現實際上具有某種虛假的成份。在道爾頓的年代，進行化學實驗的儀器與設備還十分簡陋。到了二十世紀，有很多對於科學史有興趣的科學家嘗試著按照道爾頓當年的記載，運用當時的儀器來重複道爾頓的實驗。這些科學家的結論是：以道爾頓當時的條件，他決不可能做出如此精確的實驗。因此他們認為，幾乎可以肯定的是，當時道爾頓實際上「人為地」改造了實驗資料來為他的結論辯護，儘管他的結論仍然是具有劃時代意義的。

2018年十月時哈佛醫學院的知名心臟專家Anversa被爆出其所著的31篇論文皆涉及實驗數據造假，而校方經決議後撤回他所有論文，但心肌幹細胞造假這事件也反映了一個問題，實驗科學的數據如果審稿人不親自重複一遍可能也很難發現有造假，而我們通常也會傾向於相信權威。

我們在日常生活中常常會遇到很多「統計數據」，許多人更是開口閉口地提到「大數據」。甚至有人認為信數據者得永生，這些數據主義的人們覺得宇宙是由資料流所組成的，任何現象或實體的價值就在於對資料處理的貢獻。而在本文中給大家介紹了一些不合適的統計學方法和忘記因果關係所導致的謬誤，最後還指出權威學者也有造假的可能，我們不該迷信權威，期許大家在大數據時代都能不被統計學給誤導！

參考資料：

相關標籤：

熱門標籤：

文章難易度

剛好

太難

所有討論 0

登入與大家一起討論

活躍星系核

756 篇文章・ 73 位粉絲

活躍星系核（active galactic nucleus, AGN）是一類中央核區活動性很強的河外星系。這些星系比普通星系活躍，在從無線電波到伽瑪射線的全波段裡都發出很強的電磁輻射。本帳號發表來自各方的投稿。附有資料出處的科學好文，都歡迎你來投稿喔。 Email: contact@pansci.asia

RELATED 相關文章

什麼是「生命親緣樹」？古菌啟發人類對火星生命的想像——《穿越 4.7 億公里的拜訪》

揭露蜜蜂的防疫策略！——保持「社交距離」如何阻斷寄生蟲在巢內傳播？

現實中的「沙丘行星」：為何火星上有颳不完的塵暴？——《穿越 4.7 億公里的拜訪》

我們都是火星人？論火星隕石為地球生命播種的可能——《穿越 4.7 億公里的拜訪》

文字

人體解析生命奧祕醫療健康

揭開人體的基因密碼！——「基因定序」是實現精準醫療的關鍵工具

科技魅癮・2021/11/16 ・1998字・閱讀時間約 4 分鐘

為什麼有些人吃不胖，有些人沒抽菸卻得肺癌，有些人只是吃個感冒藥就全身皮膚紅腫發癢？這一切都跟我們的基因有關！無論是想探究生命的起源、物種間的差異，乃至於罹患疾病、用藥的風險，都必須從了解基因密碼著手，而揭開基因密碼的關鍵工具就是「基因定序」技術。

基因定序對人類生命健康的意義

在歷史上，DNA 解碼從 1953 年的華生（James Watson）與克里克（Francis Crick）兩位科學家確立 DNA 的雙螺旋結構，闡述 DNA 是以 4 個鹼基（A、T、C、G）的配對方式來傳遞遺傳訊息，並逐步發展出許多新的研究工具；1990 年，美國政府推動人類基因體計畫，接著英國、日本、法國、德國、中國、印度等陸續加入，到了 2003 年，人體基因體密碼全數解碼完成，不僅是人類探索生命的重大里程碑，也成為推動醫學、生命科學領域大躍進的關鍵。原本這項計畫預計在 2005 年才能完成，卻因為基因定序技術的突飛猛進，使得科學家得以提前完成這項壯舉。

提到基因定序技術的發展，早期科學家只能測量 DNA 跟 RNA 的結構單位，但無法排序；直到 1977 年，科學家桑格（Frederick Sanger）發明了第一代的基因定序技術，以生物化學的方式，讓 DNA 形成不同長度的片段，以判讀測量物的基因序列，成為日後定序技術的基礎。為了因應更快速、資料量更大的基因定序需求，出現了次世代定序技術（NGS），將 DNA 打成碎片，並擴增碎片到可偵測的濃度，再透過電腦大量讀取資料並拼裝序列。不僅更快速，且成本更低，讓科學家得以在短時間內讀取數百萬個鹼基對，解碼許多物種的基因序列、追蹤病毒的變化行蹤，也能用於疾病的檢測、預防及個人化醫療等等。

在疾病檢測方面，儘管目前 NGS 並不能找出全部遺傳性疾病的原因，但對於改善個體健康仍有積極的意義，例如：若透過基因檢測，得知將來罹患糖尿病機率比別人高，就可以透過健康諮詢，改變飲食習慣、生活型態等，降低發病機率。又如癌症基因檢測，可分為遺傳性的癌症檢測及癌症組織檢測：前者可偵測是否有單一基因的變異，導致罹癌風險增加；後者則針對是否有藥物易感性的基因變異，做為臨床用藥的參考，也是目前精準醫療的重要應用項目之一。再者，基因檢測後續的生物資訊分析，包含基因序列的註解、變異位點的篩選及人工智慧評估變異點與疾病之間的關聯性等，對臨床醫療工作都有極大的助益。

建立屬於臺灣華人的基因庫

每個人的基因背景都不同，而不同族群之間更存在著基因差異，使得歐美國家基因庫的資料，幾乎不能直接應用於亞洲人身上，這也是我國自 2012 年發起「臺灣人體生物資料庫」（Taiwan biobank），希望建立臺灣人乃至亞洲人的基因資料庫的主因。而 2018 年起，中央研究院與全臺各大醫院共同發起的「臺灣精準醫療計畫」（TPMI），希望建立臺灣華人專屬的基因數據庫，促進臺灣民眾常見疾病的研究，並開發專屬華人的基因型鑑定晶片，促進我國精準醫療及生醫產業的發展。

目前招募了 20 萬名臺灣人，這些民眾在入組時沒有被診斷為癌症患者，超過 99％是來自中國不同省分的漢族移民人口，其中少數是臺灣原住民。這是東亞血統個體最大且可公開獲得的遺傳數據庫，其中，漢族的全部遺傳變異中，有 21.2％的人攜帶遺傳疾病的隱性基因；3.1％的人有癌症易感基因，比一般人罹癌風險更高；87.3％的人有藥物過敏的基因標誌。這些訊息對臨床診斷與治療都相當具實用性，例如：若患者具有某些藥物不良反應的特殊基因型，醫生在開藥時就能使用替代藥物，避免病人服藥後產生嚴重的不良反應。

基因時代大挑戰：個資保護與遺傳諮詢

雖然高科技與大數據分析的應用在生醫領域相當熱門，但有醫師對於研究結果能否運用在臨床上，存在著道德倫理的考量，例如：研究用途的資料是否能放在病歷中？個人資料是否受到法規保護？而且技術上各醫院之間的資料如何串流？這些都需要資通訊科技（ICT）產業的協助，而醫師本身相關知識的訓練也需與時俱進。對醫院端而言，建議患者做基因檢測是因為出現症狀，希望找到原因，但是如何解釋以及病歷上如何註解，則是另一項重要議題。

從人性觀點來看，在技術更迭演進的同時，對於受測者及其家人的心理支持及社會資源是否相應產生？回到了解病因的初衷，在知道自己體內可能有遺傳疾病的基因變異時，家庭成員之間的情感衝擊如何解決、是否有對應的治療方式等，都是值得深思的議題，也是目前遺傳諮詢門診中會詳細解說的部分。科技的初衷是為了讓人類的生活變得更好，因此，基因檢測如何搭配專業的遺傳諮詢系統，以及法規如何在科學發展與個資保護之間取得平衡，將是下一個基因時代的挑戰。