「一沙見世界, 一花視天堂, 無限含於掌, 須臾納永恆。」
威廉. 布萊克(William Blake)

想像你在數線上隨意滑動一支沒有厚度的標尺,不論標尺停在何處,總能將這條向兩端無限延伸的數線分割成互不相屬的兩邊。對於我們已知的有理數,它們會在數線上閃爍出細微的光芒,不論標尺停在何處,左右兩邊的有理數會以不同顏色的光亮顯現,所以你可以清楚地分辨標尺所在的位置。比如當你停在原點0時,你會發現所有負有理數在標尺左邊閃著金光,而所有正有理數則在標尺右邊閃著銀光,而無厚度的標尺正是不同光色的分界處。
我們把左邊閃著金光的光點命名為A集合,而把右邊閃著銀光的光點稱為B集合,於是序對(A, B)就是所有光點的總集。你既可以說是這個標尺所在的點位決定了左右兩邊的分割(A, B),但同樣可以說特定的分割(A, B)決定了標尺的落點。於是我們發現,一個點不只是一個點,它也相當於左集合A裡無限個發出金色光芒的有理數,點與分割相互決定了對方的存在。這正是為何戴德金左集合可以作為某個實數的身分證或認證條碼,因而被用來作為實數的定義,戴德金切割把我們帶入一個全新的世界。
讓我們頭痛萬分的無理數瞬間找到了歸宿,因為我們用戴德金左集合逼它們現形,可是我們原本熟知的有理數卻出了問題,因為我們忽然發現它們有了兩種定義,因而變成兩種事物。比如以自然數2來說,它原本的定義是 {0, 1} ,也就是由0和1為成員所形成的集合,其存在被配對公設所確認。但當我們用戴德金左集合來重新定義實數時,它變成了 {q ∈ Q〡q < 2} ,也就是所有小於2的有理數的集合,一瞬間它的成員數從2個變成無限多個!
如果你懷疑這只是個別現象的話,那我們可以逐一檢查每個自然數,比如5, 37或102,你會發現同樣的情況也發生在它們身上,自然數們脫離了原來定義的軌道,戴德金切割讓它們具有了「第二重身分」。分數型式的有理數m/n 也無法倖免,它們的戴德金左集合也與原先用序對的對等類(equivalence class of the ordered pair(m, n) )所下的定義不同。但我們並不打算在此介紹序對對等類所定義的m/n及其運算規則,只是說明用戴德金左集合重新界定實數之後,雖然定義出了原先沒有的無理數,但原本的有理數卻似乎陷入「人格分裂」的窘境。
本來我們的如意算盤是用口袋裡已有的有理數Q (由序對對等類定義)來定義出無理數,在製造出無理數集合I之後,取其聯集Q ∪I 得到實數集合R = Q ∪I。但現在計畫卻泡湯了,我們雖然用戴德金左集合製造出無理數,但原先的有理數卻「質變」了。
要解決這個難題就必須釐清一個觀念,那就是我們無法直接將原本的有理數納入戴德金左集合系統。對於新定義的實數系統來說,原本的有理數並非它的子系統(sub-system),所以也無法直接取它們的聯集Q ∪I來得到實數集合R。這就像是一棟樓房有許多樓層一樣,戴德金左集合所定義的系統和原先的有理數系統不在同一樓層,否則就會造成數系的雙重定義問題。如果把經由戴德金左集合所定義出來的實數看作成品的話,那原先的有理數就相當於原材料,我們透過原材料製作出新的成品(戴德金實數)。
為了更明確這種理論系統的層級差異,我們將實數的一般定義形式r 寫成:
r = {q〡P (q) 且 q ∈ Q}
其中P (q) 為描述某些與q性質相關的邏輯句式。
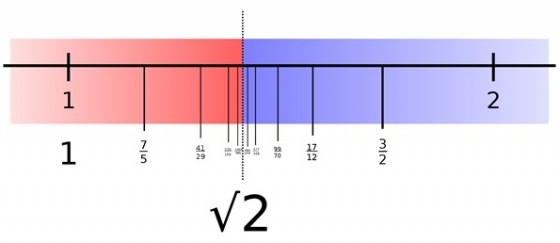
用上篇文章的例子來說,若P (q)為「q2 < 2 或 q為負數」這個句式,則r 就是指√2。若將P (q) 改為q < 3,則r 就是指3。
從這個定義形式可以看出戴德金實數與之前的有理數之間存在差別。原本的有理數q ∈ Q屬於前一個定義系統裡的理論存在項,而戴德金實數則是採用先前系統的存在項之後才定義出來的,它們屬於後一個系統(由紅字的r 所構成),也就是它們分屬於不同的理論系統或系統層級。在這樣的系統層級中,q並不等於q。q是前一個系統內的成員,它們就好像是一堆原始材料,用來建構另一個系統層級內的戴德金實數q。經由這樣的分析,我們得以擺脫同一個數卻有兩種不同定義的困境。
這就好比有天忽然修改了法律,一切原本屬於個人(自然人)能夠從事的行為現在都必須由法人來執行,包括簡單的商品購買或購買房產以及基本資料登記等等,現在都必須以法人的名義來行使了。當然為了便民,所以新的法律也允許原先的自然人用原本的名字登記為法人,然後重新占有財產,但之後的占有關係就要受到新法律的規範了。
比如有一個叫金正恩的人之前用自己的名義買了一棟房子,但根據新的法律,現在個人不能夠再以自然人的形式來擁有房產,所以他可以成立一家公司或成立一個基金會來重新占有這棟房子。但這個金正恩覺得這間房子只是供自住並沒有商業運作上的節稅問題, 所以不想用公司或其他法人形式來登記,這太麻煩了。還好根據新法律,他可以將原先的名字重新登記成法人來占有原本的房屋,這個新法人的內部結構也還是歸他自己控制,名字也叫金正恩,只不過現在他對房屋的占有受新法律對法人的規範所制約罷了。因此現在有了兩個金正恩,一個是原本那個自然人金正恩,根據新法律他無法再擁有房屋了。另一個是受到新法律規定而不得不重新登記成法人的那個金正恩法人,它(法人)可以擁有房產。我們可以用以上的方式來理解不同系統層級中的q和q之間的關係。
邏輯困境被我們用系統層級的差異解決了,但這樣定義出來的戴德金實數能符合原先我們期待它們應該具有的數學性質嗎?那就讓我們來看看如何正確定義它們的基本性質和運算吧。兩個戴德金實數r 和s 在甚麼條件下相等呢?既然實數被定義為戴德金左集合,那麼我們可以推測,如果兩個實數相等的話那就等於說兩個左集合也相等。果不其然,對於所有有理數q,如果滿足q ∈r 若且唯若q ∈s這個條件,也就是兩個左集合r 和s有相同元素的話,那我們就說戴德金實數r =s 。
依照同樣的原理,我們可以定義出r ≤ s 和r < s。按照相同的思路,由戴德金左集合定義出來的的實數r若要比s小,那必然會滿足r ⊆ s的要求了。因此對任何有理數q,若q ∈r 則q ∈s這個條件滿足的話,我們就將其定義為r ≤ s。如果再加上r ≠ s這個條件,那我們就可以定義出r < s了。
你可以自己檢驗一下加法的定義r +s ={p + q〡p∈r 且 q∈ s}是否符合我們對一般算術加法的要求?其中p + q的部分就是我們原來熟悉的有理數的加法,得出答案之後再看看r +s的戴德金左集合是否能得出與原本算術規則符合的另一個實數?至於乘法的定義稍嫌複雜就不在此贅述了。但可以預先通告的是這樣定義出來的戴德金實數完全滿足16個實數公設,而我們目前就是用這16條公設來建構出整個實數系的。
戴德金切割所定義的實數雖然矗立在另一個系統層級上,但它們能夠滿足16個公設而成為建構現代實數系的基石,所以值得多花這些篇幅來概述。除此之外,我們引介戴德金切割的目的在於這個觀念可以幫助我們輕易地解決實數R和自然數冪集合P(N) 之間的尺寸關係,那是我們困惑已久的問題。那麼,這兩種不可數無限集合到底是否等量呢?這就只有等下回再分解了!