有理數是能夠用分數形式m/n來表達的數,其中m和n為整數且n ≠ 0。雖然到現在為止我們的公設只建構出自然數,但用自然數來建構有理數並不困難,它的基本概念是取序對(m, n)的型態來定義有理數。由於自然數和序對我們都已相當熟悉,況且有理數的概念在直觀上也很容易理解,因此我們並不打算在此介紹和證明如何用自然數定義出有理數的技術細節。可是對實數裡的「另一半」— 無理數來說,情況就大不相同了。
我們很難想像給出任意兩條線段,居然會找不到另一個線段作為衡量前兩者的共同單位。對有些情況來說,不論我們上天下地,卻永遠找不到這個共同單位,這在幾何學上叫做不可通約(incommensurable)。但這種讓古希臘畢氏學派震驚的「知識瘟疫」卻並非雪山靈芝而是隨處可見,比如從任一個正方形劃出對角線就可以根據畢氏定理12 +12 = x2 得出√2這個數,而√2就無法表示成m/n的分數形式。
根據傳說,畢氏學派把無理數的發現視為最高機密並禁止門徒對外洩漏,然而希臘的「斯諾登」希帕蘇斯先生卻冒死對外公佈了這個秘密,因而遭到如同黑社會懲罰臥底一般的待遇—扔到海裡餵魚。我們不知道這個傳說的真實性如何,但這意謂在某個歷史時期公佈某項知識成果的後果可能和今天所謂「洩漏國家機密」的後果沒兩樣。
既然無理數的性質那麼「無理」,可見要用自然數或有理數的概念來對其進行嚴格定義是很困難的。但現代實數系的兩位奠基者康托和德國數學家戴德金(R. Dedekind)雖然從不同的角度和進路用不同的方法來破解這個問題,但他們在推進人類對實數的理解時也同時發展了集合的概念。現在就來看看戴德金最重要的發明—如何用有理數來重新定義實數(因而自然把無理數也包含進去)的偉大創見,它稱之為戴德金切割(Dedekind cut) 。
由於有理數建立在自然數的基礎上,而自然數又建立在集合論的公設上,所以它們早已取得明確的「身分」,現在身分不明且難以被直觀掌握的就剩下無理數了。戴德金切割到底是個甚麼東西呢?首先來看看切割(cut)的定義:
一個切割就是一個序對(A, B),其中A, B ≠ Ø且A 和B不相交(也就是A ∩ B = Ø)。此外A ∪ B = P,也就是說切割是把某個集合P給切開,分成沒有共同元素的A, B兩半。
第二個條件是A的所有元素都比B的元素小,也就是說從數線的觀點來看,A的元素都在B元素的左邊。
滿足上述兩個條件的序對(A, B)就是一個對P集合的切割。由於序對(A, B)是集合,所以一個切割本身就相當於集合。而所謂戴德金切割必須加上第三個條件,那就是序對左邊的A集合沒有最大元素。它的直觀意思是說如果我們用某個點來切開P集合,那麼這個點不在A裡面。
我們現在手頭的武器是全部的有理數,所以可以把集合P用全體有理數Q來替代,那麼戴德金切割就成了把全部有理數分成A, B兩半的序對(A, B) ,所以A ∪ B = Q。由於A與B不相交,因此確定了其中一邊也同時確定了另一邊,習慣上我們用序對左邊的集合A來定義實數,稱之為戴德金左集合(Dedekind left set)。也就是說一個實數就是一堆有理數所形成的戴德金左集合,而全體實數就是這些戴德金左集合所形成的集合。
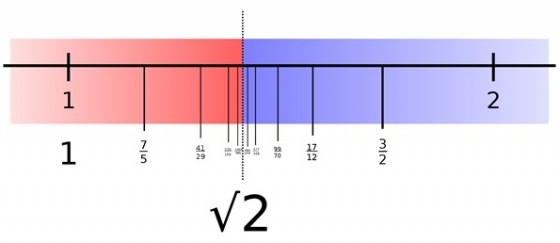
為了更容易理解戴德金左集合的定義,我們用√2來具體說明。如下圖所示,雖然目前我們尚不知道無理數√2的定義,但我們可以利用畢氏定理將邊長為1的正方形取對角線,然後用圓規將與對角線等長的線段畫到數線上,這樣就標出了長度相當於√2在數線上的位置。
我們發現它正好把大於此數和小於此數的有理數Q分成兩半,紅色部分為所有小於√2的有理數,而藍色部分則為所有大於√2的有理數。紅色部分和藍色部分沒有共同成員,它們的聯集等於全體有理數,所以顯然滿足戴德金切割的第一個條件。而紅色集合內的有理數顯然都在藍色成員的左邊,因此滿足第二個條件。此外以√2為分界的戴德金左集合(紅色部分)顯然沒有最大元素,因為作為分界的√2不屬於有理數,所以第三個條件也滿足了,它是一個戴德金切割。
接下來就看怎麼樣來定義這個特殊的戴德金左集合。有人會說這很容易啊,只要定義 A = {q〡q <√2 且 q∈ Q}不就得了?但請注意,我們目前還不知道√2是甚麼,我們只知道有理數是甚麼東東,正絞盡腦汁想把√2的定義找出來,所以上面對A的定義等於是拿未知的東西來定義未知,也是拿尚待定義的東西來作為定義,這是不可接受的。
為了要避開這種循環定義,我們把上式梢作修改成
A = {q〡q2 < 2 且 q ∈ Q}
這樣一來所有的條件就都符合有理數的規定範圍。但仔細一看問題又來了,因為戴德金左集合會一直往負的方向無限延伸,因此越往左其平方值會越來越大,比如:
-2 ∈ Q 且-2∈ A,但顯然 (-2)2 > 2,這與A的規定顯然不合。該怎麼辦呢? 只要利用邏輯概念將小於√2的正負數分開處理就行了,因此我們重新把A定義為
A = {q ∈ Q 〡q2 < 2 或 q為負數}
如果有耐心地依序檢查,會發現這個定義符合戴德金切割的條件,因而正是用來定義√2的戴德金左集合。
這個看似古怪的定義讓我們可以單憑有理數重新定義出所有實數(尤其是無理數),而且這樣定義出來的無理數完全可以滿足實數所須具備的各種運算和性質,真可謂鬼斧神工。更重要的是透過戴德金切割我們發現,無限集合居然可以用來標定某個特定實數,這實在太神奇了。戴德金左集合宛如實數的基因密碼,透過對這些密碼的識別和辨認達到對實數本身身分的確認。僅管構成生物基因的分子為數眾多但卻是有限的,然而每個戴德金左集合的元素個數卻都是無限,任何一個實數都可以用某個無限集合來唯一確定。
如果你還沒有意識到此中令人驚奇之處,那麼我們再把戴德金切割比喻成商品的條碼,每一個條碼都指向一種特殊的商品。讓我們感到驚異的是,在實數的定義裡,構成每個條碼的信息單元(有理數)竟然不是有限而是無限。
雖然戴德金切割用這種有理數的「無限條碼」奇蹟似地界定出實數,但有些數的意義似乎產生了奇怪的病變。比如自然數0原來是用空集合來定義,所以0 = { } ,可是在戴德金左集合的新包裝下,0 不再是空無一物而成了 {q〡q ∈ Q 且q<0} ,這到底是怎麼回事呢?難道同一個數可以同時由兩個集合來定義嗎?要解開這個難題,這就只有等下回再分解了!