文 / 翁昌黎(《孔恩vs.波普》中文譯者)
「聞眾生界不可思議…聞法界不可思議… 聞虛空界不可思議」—大方廣佛華嚴經
如果沒有偉大而極富想像力的數學家康托,那我們迄今為止可能還以為無限大或無窮大就是最大的集合,而且它只有一種型態,就是從1、2、3、4、5一直往下數直到無窮無盡的龐大集合。但令人疑惑的是,所有自然數的集合既然都已經是無限大了,難道還能比它更大?不錯,康托在西元1874年不但找出這個更大的集合,而且還證明了它!
要理解這個比無限大還大的神奇之物,那就要請出ZF集合論的第7個公設—冪集合公設(Axiom of Power Set):
ZF7 ∀X ∃Y ∀z [z ∈ Y ↔ ∀ u (u∈z → u∈ X)]
這個公設看起來有點複雜,但我們如果引入一個關於子集合(subset)的定義就能讓問題簡化許多。以上句式中的 z 是 X 的子集,寫成 z ⊆ X ,它的定義是:∀ u (u∈z → u∈ X),這恰好就是冪集合公設的後半部分。我們先按以上定義把冪集合公設改寫成比較簡單的形式:
ZF7 (1) ∀X ∃Y ∀z [z ∈ Y ↔ z⊆ X]
經過上面的簡化之後,冪集合公設的意思是:如果我們手頭上已經有某個 X 集合,那麼由 X 集合的所有子集合可以形成另一個新的集合 Y。
這個公設讓我們又多了一個製造集合的方法,也就是把手頭上現成集合的子集合全部抓出來,將這些子集合作為元素來形成一個新集合,這就是ZF7所要做的事情。但我們還沒解釋什麼是子集合,根據定義,如果∀ u (u∈z → u∈ X)成立,也就是凡 z 的成員都是 X 的成員的話,那 z 就是 X 的子集合。
我們用個簡單的小集合作例子就容易明白了。假設有個包含1, 2, 3三個自然數的集合當作 X = {1, 2, 3} 。那 X 的子集合是甚麼? 首先 {1, 2, 3 } 是它自己的子集合。因為在這種情況下 z = X ,所以∀ u (u∈ X → u∈ X) 顯然成立,這就相當於說在 X 裡邊的元素必定在 X 裡邊一樣的廢話。進一步觀察發現,將 X= { 1, 2, 3 } 中的成員拿掉幾個,殘留的集合都是 X 的子集合,比如說 {1}、{1, 2}和 {2, 3}等都是。將這些子集合全部蒐集起來登記在 Y 底下所形成的集合就是 X 的冪集合。在以上 X= {1, 2, 3}的例子裡:
Y = { {1, 2, 3}, {1, 2}, {2, 3}, {1, 3}, {1}, {2}, {3}, { } }
細心的讀者會發現裡面有個空集合,為了邏輯與數學上的嚴密性有必要解釋一下為什麼空集合也是 X 的子集合,但這麼重要的關鍵在許多數學課本裡卻提都不提。
剛剛談到 z 是 X 的子集合是用∀u (u∈z → u∈ X) 來定義,那我們就把空集合 { } 放到定義中看看符不符合子集合的規定。那就是要看 ∀ u (u∈{ } → u∈ {1, 2, 3})是否為真? 因為{ }中空空如也什麼都沒有,所以條件句u∈{ } → u∈ {1, 2, 3} 的前件u∈{ }對任何 u 來說都為假,因為不存在任何集合能滿足這個條件。因此根據實質涵蘊 → 的定義,前件為假則整個條件句為真,所以∀ u (u∈ { } → u∈ {1, 2, 3}) 為真。既然空集合滿足子集合成立的條件,所以我們可以安心地將其納入冪集合的成員裡頭。
好了,現在我們有了製造冪集合的方法,但要它有何用呢? 它有什麼神妙之處? 粗略觀察可以發現冪集合的成員數比原來集合的成員數還多一些,X 集合有3個成員而它的羃集合 Y 有8個成員。那麼如果我們拿剛剛被無限公設所承認的,包含所有自然數的集合來製造冪集合的話會發生什麼事呢?
在有限集合的情況下,冪集合 Y 的成員數鐵定比原來集合 X 的成員數還多。直覺似乎告訴我們,既然所有自然數所形成的集合其成員數量已經是無限大,那麼它的冪集合成員數量頂多也是無限大,因為不可能有比無限大更大的數量了。照理說兩者的成員數目應該一樣多才對,照這麼說的話那麼ZF7並沒有提供比ZF6更新鮮的東西。
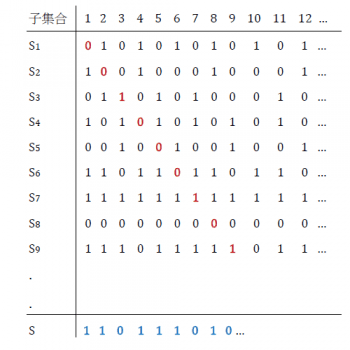
但在羅素詭論的歷史教訓下,我們在數學領域還是對直覺適度存疑比較妥當。還是按照這個假設來做個實驗,看看 X 集合的冪集合 Y 所擁有的成員數目是否跟 X 集合一樣多。方法是這樣的:假設 Y 的成員和自然數的無限集合一樣多,那它的每個成員必然可以跟自然數對上號,那表示我們可以把它們 ( X 所有的子集合) 用S1, S2, S3,…, Sn,… 來編號排列,其中每個Sk (k=1, 2, 3…)都是 X 的子集合。可以用下表來說明:
現在來解釋一下這個表的意義。因為我們是把整個自然數集合拿來選取子集合,所以凡是被選進某個子集合的自然數就打上1,沒選上的就打 0,這樣每個子集合就可以用由 0, 1所形成的無窮序列來表示,每個序列都被標上序號。我們發現將這個子集合序列的對角線連起來會形成一個獨特的0, 1串列,比如在我們以上的例子裡,對角線串列是用紅色數目字表示的 001000101 …。我們利用這個串列來做個改裝,將其中凡是出現 0 的地方都改成1,凡是出現1的地方都改成 0,這樣就得到一個新的串列(上表藍字部分)S = 110111010…。
這個串列S有一個奇妙的特性,那就是它居然不落在無窮序列 Sk(k=1, 2, 3… ) 裡面!為什麼呢? 仔細觀看S的變化可以發現,它的第一個數字與S1 不同,所以S不是S1,第二個數字與S2 不同,所以S也不是S2,第三個數字與S3 不同…,也就是說S不可能出現在 Sk(k=1, 2, 3…) 這個無窮序列裡。
聰明的你可能會說,沒關係,把這個不合群的S重新放到Sk裡不就得了!反正Sk是個無窮序列,多一個不多,少一個不少,這樣以上的難題就解決了。先別高興太早,當你把這個S放進無窮序列之後,我們依然可以如法泡製,用同樣方法畫出一條新的對角線,然後得出一個新的0, 1串列,再將其中的 0轉成1,1再轉成0,於是又得到一個新串列S’。新串列S’ 仍然不在新形成的Sk裡,正所謂魔高一尺道高一丈上有政策下有對策,永遠會出現漏網之魚。
但這隻咬破魚網的小魚S意味著什麼呢? 千萬別小看它,它意味著全體自然數的集合還不夠大,自然數的無限集合無法窮盡由它所形成的冪集合,偉大的知識革命就在那條魚出現之處完成了。它意味自然數冪集合的成員數目居然比自然數的數目還要多!這是個革命性的發現,利用神奇的對角線論證,康托證明了存在著比全體自然數集合—所謂的可數無限(countable infinity)集合還要大的不可數無限(uncountable infinity)集合。跟這個發現相比,哥倫布所謂的發現新大陸簡直就像扮家家酒。
無限公設ZF6送給我們第一個無限集合,但它只是可數的無限。ZF7帶給我們製造冪集合的方法,把ZF6的無限集合當成原料,利用ZF7這台神奇數學機器居然成功提煉出超乎想像的不可數無限集合,並將我們的數學知識帶到一個前所未有的嶄新世界。