這個九九乘法表你小學沒背過！吠陀方形的千年奧秘

• 作者／賴昭正｜前清大化學系教授、系主任、所長；合創科學月刊

我擔心人工智慧可能會完全取代人類。如果人們能設計電腦病毒，那麼就會有人設計出能夠自我改進和複製的人工智慧。 這將是一種超越人類的新生命形式。

——史蒂芬．霍金（Stephen Hawking）　英國理論物理學家

大約在八十年前，當第一台數位計算機出現時，一些電腦科學家便一直致力於讓機器具有像人類一樣的智慧；但七十年後，還是沒有機器能夠可靠地提供人類程度的語言或影像辨識功能。誰又想到「人工智慧」（Artificial Intelligent，簡稱 AI）的能力最近十年突然起飛，在許多（所有？）領域的測試中擊敗了人類，正在改變各個領域——包括假新聞的製造與散佈——的生態。

圖形處理單元（graphic process unit，簡稱 GPU）是這場「人工智慧」革命中的最大助手。它的興起使得九年前還是個小公司的 Nvidia（英偉達）股票從每股不到 $5，上升到今天（5 月 24 日）每股超過 $1000（註一）的全世界第三大公司，其創辦人（之一）兼首席執行官、出生於台南的黃仁勳（Jenson Huang）也一躍成為全世界排名 20 內的大富豪、台灣家喻戶曉的名人！可是多少人了解圖形處理單元是什麼嗎？到底是時勢造英雄，還是英雄造時勢？

在回答這問題之前，筆者得先聲明筆者不是學電腦的，因此在這裡所能談的只是與電腦設計細節無關的基本原理。筆者認為將原理轉成實用工具是專家的事，不是我們外行人需要了解的；但作為一位現在的知識分子或公民，了解基本原理則是必備的條件：例如了解「能量不滅定律」就可以不用仔細分析，即可判斷永動機是騙人的；又如現在可攜帶型冷氣機充斥市面上，它們不用往室外排廢熱氣，就可以提供屋內冷氣，讀者買嗎？

CPU 與 GPU

不管是大型電腦或個人電腦都需具有「中央處理單元」（central process unit，簡稱 CPU）。CPU 是電腦的「腦」，其電子電路負責處理所有軟體正確運作所需的所有任務，如算術、邏輯、控制、輸入和輸出操作等等。雖然早期的設計即可以讓一個指令同時做兩、三件不同的工作；但為了簡單化，我們在這裡所談的工作將只是執行算術和邏輯運算的工作（arithmetic and logic unit，簡稱 ALU），如將兩個數加在一起。在這一簡化的定義下，CPU 在任何一個時刻均只能執行一件工作而已。

在個人電腦剛出現只能用於一般事物的處理時，CPU 均能非常勝任地完成任務。但電腦圖形和動畫的出現帶來了第一批運算密集型工作負載後，CPU 開始顯示心有餘而力不足：例如電玩動畫需要應用程式處理數以萬計的像素（pixel），每個像素都有自己的顏色、光強度、和運動等, 使得 CPU 根本沒辦法在短時間內完成這些工作。於是出現了主機板上之「顯示插卡」來支援補助 CPU。

1999 年，英偉達將其一「具有集成變換、照明、三角形設定／裁剪、和透過應用程式從模型產生二維或三維影像的單晶片處理器」（註二）定位為「世界上第一款 GPU」，「GPU」這一名詞於焉誕生。不像 CPU，GPU 可以在同一個時刻執行許多算術和邏輯運算的工作，快速地完成圖形和動畫的變化。

依序計算和平行計算

一部電腦 CPU 如何計算 7×5+6/3 呢？因每一時刻只能做一件事，所以其步驟為：

• 計算 7×5；
• 計算 6/3；
• 將結果相加。

總共需要 3 個運算時間。但如果我們有兩個 CPU 呢？很多工作便可以同時（平行）進行：

• 同時計算 7×5 及 6/3；
• 將結果相加。

只需要 2 個運算時間,比單獨的 CPU 減少了一個。這看起來好像沒節省多少時間，但如果我們有 16 對 a×b 要相加呢？單獨的 CPU 需要 31 個運算的時間（16 個 × 的運算時間及 15 個 + 的運算時間），而有 16 個小 CPU 的 GPU 則只需要 5 個運算的時間（1 個 × 的運算時間及 4 個 + 的運算時間）！

現在就讓我們來看看為什麼稱 GPU 為「圖形」處理單元。圖一左圖《我愛科學》一書擺斜了，如何將它擺正成右圖呢？ 一句話：「將整個圖逆時針方向旋轉 θ 即可」。但因為左圖是由上百萬個像素點（座標 x, y）組成的，所以這句簡單的話可讓 CPU 忙得不亦樂乎了：每一點的座標都必須做如下的轉換

x’ = x cosθ + y sinθ

y’ = -x sinθ+ y cosθ

即每一點均需要做四個 × 及兩個 + 的運算！如果每一運算需要 10^-6 秒，那麼讓《我愛科學》一書做個簡單的角度旋轉，便需要 6 秒，這豈是電動玩具畫面變化所能接受的？

人類的許多發明都是基於需要的關係，因此電腦硬件設計家便開始思考：這些點轉換都是獨立的，為什麼我們不讓它們同時進行（平行運算，parallel processing）呢？於是專門用來處理「圖形」的處理單元出現了——就是我們現在所知的 GPU。如果一個 GPU 可以同時處理 10⁶ 運算，那上圖的轉換只需 10^-6 秒鐘！

GPU 的興起

GPU 可分成兩種：

• 整合式圖形「卡」（integrated graphics）是內建於 CPU 中的 GPU，所以不是插卡，它與 CPU 共享系統記憶體，沒有單獨的記憶體組來儲存圖形／視訊，主要用於大部分的個人電腦及筆記型電腦上；早期英特爾（Intel）因為不讓插卡 GPU 侵蝕主機的地盤，在這方面的研發佔領先的地位，約佔 68% 的市場。
• 獨立顯示卡（discrete graphics）有不與 CPU 共享的自己專用內存；由於與處理器晶片分離，它會消耗更多電量並產生大量熱量；然而，也正是因為有自己的記憶體來源和電源，它可以比整合式顯示卡提供更高的效能。

2007 年，英偉達發布了可以在獨立 GPU 上進行平行處理的軟體層後，科學家發現獨立 GPU 不但能夠快速處理圖形變化，在需要大量計算才能實現特定結果的任務上也非常有效，因此開啟了為計算密集型的實用題目編寫 GPU 程式的領域。如今獨立 GPU 的應用範圍已遠遠超出當初圖形處理，不但擴大到醫學影像和地震成像等之複雜圖像和影片編輯及視覺化，也應用於駕駛、導航、天氣預報、大資料庫分析、機器學習、人工智慧、加密貨幣挖礦、及分子動力學模擬（註三）等其它領域。獨立 GPU 已成為人工智慧生態系統中不可或缺的一部分，正在改變我們的生活方式及許多行業的遊戲規則。英特爾在這方面發展較遲，遠遠落在英偉達（80%）及超微半導體公司（Advance Micro Devices Inc.，19%，註四）之後，大約只有 1% 的市場。

事實上現在的中央處理單元也不再是真正的「單元」，而是如圖二可含有多個可以同時處理運算的核心（core）單元。GPU 犧牲大量快取和控制單元以獲得更多的處理核心，因此其核心功能不如 CPU 核心強大，但它們能同時高速執行大量相同的指令，在平行運算中發揮強大作用。現在電腦通常具有 2 到 64 個核心；GPU 則具有上千、甚至上萬的核心。

結論

我們一看到《我愛科學》這本書，不需要一點一點地從左上到右下慢慢掃描,即可瞬間知道它上面有書名、出版社等，也知道它擺斜了。這種「平行運作」的能力不僅限於視覺，它也延伸到其它感官和認知功能。例如筆者在清華大學授課時常犯的一個毛病是：嘴巴在講，腦筋思考已經不知往前跑了多少公里，常常為了追趕而越講越快，將不少學生拋到腦後！這不表示筆者聰明，因為研究人員發現我們的大腦具有同時處理和解釋大量感官輸入的能力。

人工智慧是一種讓電腦或機器能夠模擬人類智慧和解決問題能力的科技，因此必須如人腦一樣能同時並行地處理許多資料。學過矩陣（matrix）的讀者應該知道，如果用矩陣和向量（vector）表達，上面所談到之座標轉換將是非常簡潔的（註五）。而矩陣和向量計算正是機器學習（machine learning）演算法的基礎！也正是獨立圖形處理單元最強大的功能所在！因此我們可以了解為什麼 GPU 會成為人工智慧開發的基石：它們的架構就是充分利用並行處理，來快速執行多個操作，進行訓練電腦或機器以人腦之思考與學習的方式處理資料——稱為「深度學習」（deep learning）。

黃仁勳在 5 月 22 日的發布業績新聞上謂：「下一次工業革命已經開始了：企業界和各國正與英偉達合作，將價值數萬億美元的傳統資料中心轉變為加速運算及新型資料中心——人工智慧工廠——以生產新商品『人工智慧』。人工智慧將為每個產業帶來顯著的生產力提升，幫助企業降低成本和提高能源效率，同時擴大收入機會。」

附錄

人工智慧的實用例子：下面一段是微軟的「copilot」代書、谷歌的「translate」代譯之「one paragraph summary of GPU and AI」。讀完後，讀者是不是認為筆者該退休了？

GPU（圖形處理單元）和 AI（人工智慧）之間的協同作用徹底改變了高效能運算領域。GPU 具有平行處理能力，特別適合人工智慧和機器學習所需的複雜資料密集運算。這導致了影像和視訊處理等領域的重大進步，使自動駕駛和臉部辨識等技術變得更加高效和可靠。NVIDIA 開發的平行運算平台 CUDA 進一步提高了 GPU 的效率，使開發人員能夠透過將人工智慧問題分解為更小的、可管理的、可同時處理的任務來解決這些問題。這不僅加快了人工智慧研究的步伐，而且使其更具成本效益，因為 GPU 可以在很短的時間內執行與多個 CPU 相同的任務。隨著人工智慧的不斷發展，GPU 的角色可能會變得更加不可或缺，推動各產業的創新和新的可能性。大腦透過神經元網路實現這一目標，這些神經元網路可以獨立但有凝聚力地工作，使我們能夠執行複雜的任務，例如駕駛、導航、觀察交通信號、聽音樂並同時規劃我們的路線。此外，研究表明，與非人類動物相比，人類大腦具有更多平行通路，這表明我們的神經處理具有更高的複雜性。這個複雜的系統證明了我們認知功能的卓越適應性和效率。我們可以一邊和朋友聊天一邊走在街上，一邊聽音樂一邊做飯，或一邊聽講座一邊做筆記。人工智慧是模擬人類腦神經網路的科技，因此必須能同時並行地來處理許多資料。研究人員發現了人腦通訊網路具有一個在獼猴或小鼠中未觀察獨特特徵：透過多個並行路徑傳輸訊息,因此具有令人難以置信的多任務處理能力。

註解

（註一）當讀者看到此篇文章時，其股票已一股換十股，現在每一股約在 $100 左右。

（註二）組裝或升級過個人電腦的讀者或許還記得「英偉達精視 256」（GeForce 256）插卡吧?

（註三）筆者於 1984 年離開清華大學到 IBM 時，就是參加了被認為全世界使用電腦時間最多的量子化學家、IBM「院士（fellow）」Enrico Clementi 的團隊：因為當時英偉達還未有可以在 GPU 上進行平行處理的軟體層，我們只能自己寫軟體將 8 台中型電腦（非 IBM 品牌！）與一大型電腦連接來做平行運算，進行分子動力學模擬等的科學研究。如果晚生 30 年或許就不會那麼辛苦了?

（註四）補助個人電腦用的 GPU 品牌到 2000 年時只剩下兩大主導廠商：英偉達及 ATI（Array Technology Inc.）。後者是出生於香港之四位中國人於 1985 年在加拿大安大略省成立，2006 年被超微半導體公司收購，品牌於 2010 年被淘汰。超微半導體公司於 2014 年 10 月提升台南出生之蘇姿豐（Lisa Tzwu-Fang Su）博士為執行長後，股票從每股 $4 左右，上升到今天每股超過 $160，其市值已經是英特爾的兩倍，完全擺脫了在後者陰影下求生存的小眾玩家角色，正在挑戰英偉達的 GPU 市場。順便一題：超微半導體公司現任總裁（兼 AI 策略負責人）為出生於台北的彭明博（Victor Peng）；與黃仁勳及蘇姿豐一樣，也是小時候就隨父母親移居到美國。

（註五）或。

延伸閱讀

• 「熱力學與能源利用」，《科學月刊》，1982 年 3 月號；收集於《我愛科學》（華騰文化有限公司，2017 年 12 月出版），轉載於「嘉義市政府全球資訊網」。
• 「網路安全技術與比特幣」，《科學月刊》，2020 年 11 月號；轉載於「善科教育基金會」的《科技大補帖》專欄。

• 文／郭君逸 │國立臺灣師範大學數學系副教授

編按：說到乘法，我們很快都會想到國小的共同回憶「九九乘法表」。背誦它對我們來說可能是一位數相乘最快的解方，多位數我們就用直式乘法運算。但如果是超超超超超超超級多位數互相相乘呢？有沒有更快的方法？

對於人腦來說可能大位數的乘法已經沒有意義，但對於電腦來說，有新的乘法方式可是大大的不一樣！三月時有數學家發表了有史以來將大數字相乘最快的新乘法方式，讓我們一起來一探究竟吧！

從「九九加法表」與「九九乘法表」談起

我們在國小時的數學，一開始就會先學「數數」，要會數 1、2、3、⋯接下來才能學加法，例如：8+5 就是 8 往後數 5 個…9, 10, 11, 12, 13，所以 8+5=13。但每次都這樣做建構式的加法太慢，成不了大事，於是大家就背了「九九加法表」（雖然老師沒提這個表，但事實上大家的確都背了！）來快速處理一位數的加法，後來再學直式加法搭配進位，就能夠計算多位數的加法。

學習乘法也是差不多的歷程。正整數的乘法其實本質就是「重複做很多次加法」，例如 6 × 4 其實就等於 6+6+6+6 或是 4+4+4+4+4+4，但很快地我們馬上就會發現這樣做建構式的乘法，速度太慢，成不了大事，於是大家就背了「九九乘法表」來快速處理一位數的乘法，然後再學直式乘法搭配進位，來處理多位數的乘法。

加法跟乘法我們都可以做到高位數，但究竟是加法比較快，還是乘法較快呢？

到底要算幾次？加法與乘法運算次數比較

若是一位數對一位數的話，當然是一樣快，因為「九九加法表」跟「九九乘法表」我們都倒背如流了；但當「2 位數加 2 位數」與「2 位數乘 2 位數」來比呢？

明顯乘法的運算次數一定比加法多，光直式乘法最後的 522+3480 就超越了 87+46 的加法數，何況還要做 7×6, 8×6, 7×4, 8×4 四次乘法；然後 7×6 與 8×6 也要做一個加法才能算出 522，7×4 與 8×4 也一樣。

一般來說 n 位數加 n 位數，連進位都算進去的話，要做 2n-1 次一位數加法；但 n 位數乘 n 位數的話，最多會用到 2n(n-1)的一位數加法，與 n² 次的一位數乘法。可見，乘法的運算次數是隨著位數的平方成長，所以計算乘法比較慢。

Karatsuba以加減法取代乘法，加快運算速度？

1960年，俄羅斯的大數學家 Andrey Kolmogorov 在一次研究討論中提出他的猜測（n 位數的乘法必須用到至少 n² 數量級的一位數乘法），例如 2 位數乘以 2 位數必須進行 4 次一位數乘法，他認為不能再快了。

結果一個禮拜後他的學生 Anatoly Karatsuba 就推翻這項猜測，找到僅需 3 次一位數乘法的計算。以 87×46 為例，Karatsuba 的方法是這樣的，先算十位相乘 8×4=32，與個位相乘 7×6=42，這個部份與傳統直式乘法一樣，但他卻只用了一次乘法就算出了 8×6和 7×4 且同時把它們加起來。我們先把傳統直式乘法改成如下：

中間的方框就是要計算 8×6 加 7×4，Karatsuba巧妙的用 (8+7)×(4+6)- 8×4-7×6 來達到同樣的效果。注意到，上式中只有第一個乘號要算，後兩個剛剛已經算過了，也就是說 Karatsuba 用一個加法與兩個減法取代了一個乘法。讀者這時可能會想說，拿一個一位數乘法去換三個加減法，又不是頭殼壞去，這樣不是反而慢嗎？

我們來看一下 4 位數的情況， 2531×1467 一樣先算 25×14 與 31×67，然後中間的 25×67+31×14 用 (25+31)×(14+67)-25×14-31×67 計算，最後加總起來。

如同前面的分析，此處一樣用到三個二位數乘法，而每個二位數乘法又用到三個一位數乘法，所以總共用到 3×3 =9 次一位數乘法。因此一般 n 位數的乘法，用這種技巧，可以只用到

3^log₂ n=n^log₂ 3=n^1.58

個一位數乘法。位數越高，用到的一位數乘法數就會越接近 n^1.58 的常數倍。對於人來說，因為把一個乘法換三個加減法，並沒有比較快，何況還要遞迴的操作；但是，對電腦而言就不是這樣了。

電腦運算的本質：二進位

電腦的本質上是二進位的系統 （哪有！我用電腦這麼多年，沒看到什麼二進位啊！那是現在電腦發展很快，事實上隨便顯示一張小圖、或一個字，背後都做了數百萬次的二進位運算。）而電腦的加法是用位元的邏輯運算來達成（也就是 AND、OR、XOR、NOT、Shift 這些東西來組成的），而位元邏輯運算超快，詳細我們就不說了，總之電腦的加法非常快。

那電腦的乘法，真的是用 Karatsuba 的方法嗎？其實也不是，我們先來看一下 8 位元的電腦怎麼做乘法好了。以 11 乘以 14 來說，化成二進位變成 00001011 與 00001110 （前面要補 0，因為 8 位元的電腦它就是用 8 個位元儲存數字。）

這不就是直式乘法嗎？這樣哪有比較快？有的。因為人類習慣十進位，所以要背「九九乘法表」；電腦用的是二進位，所以要背「一一乘法表」！！沒錯，所以等於不用背，二進位的直式乘法，其實只是被乘數的平移，然後加起來而已，換句話說，其實乘法，也是一堆位元邏輯運算而已，所以也是超快的。

那 Karatsuba 的方法用在哪呢？用在很大很大的數字相乘的時候。電腦的乘法雖快，但 8 位元電腦，最大就只能處理 2⁸－1＝255 以內的乘法，乘完後超過 255 的話就不能處理了，16位元電腦最大可以處理到 65535 以內的數，而現在的64位元電腦就可以處理到……一個非常大的數，呵呵。

那超過電腦能處理的數的話，到頭來，還是要用傳統的方法來處理，為了不要讓數字太大，我們以 8 位元的電腦為例，處理數字就會看成 256 進位來處理，533×499 就會變成

所以當數字大的時候，這時 Karatsuba 的方法就有用了。

值得一提的是，當電腦硬體從 8 位元升級到 16 位元時，軟體若沒有改成 65536 進位的話，而用 16 位元電腦來存 255 以內的數，前面就會補了更多的 0，處理起反而會浪費時間。而若軟體有跟著處理成 65536 進位的話，533×499 就會變只有位元邏輯運算而已，會超快。這就是為什麼電腦硬體剛進入 64 位元時代時，軟體沒有跟上的話，執行程式反而變慢的原因。

歷經三十年的演算法改進

OK，我們再回來乘法的問題。Karatsuba 的方法，在數字大的時候的確可以加快乘法，以一千位數的乘法來說，此法的速度大約是傳統乘法的 17 倍。

隔年，1963 年，A. L. Toom改進到了 ；後來 1966 年 Arnold Schönhage 用了新的方法推進到；1969 年 Knuth（沒錯，就大家所知道的Knuth），改進到。

後來 1971 年，Schönhage 捲土重來，與 Volker Strassen 利用快速傅立葉變換改進為 O(nlogn log logn)，此為有名的 Schönhage–Strassen algorithm，在差不多三萬位數以上的乘法，會比 Karatsuba 方法還要快。此法也是目前大數字乘法的主流，著名的梅森質數搜尋網（Great Internet Mersenne Prime Search，在 2018 年 12 月找到第 51 個）就是用 Schönhage–Strassen algorithm 來達到快速乘法。

隔了三十幾年，一直到了2007年，Martin Fürer一樣是用快速傅立葉變換，將複雜度下降到了O(n (log n) 16^log*n)，其中 log*n 就是 n 取幾次 log 會讓這個數小於 1，這是一個成長很慢的函數，基本上可以視它為常數了。

最後最後，David Harvey 與 Joris Van Der Hoeven 寫了幾篇的論文，把這個結果改成 O(n(logn)8^log*n)，然後 O(n(log n)4^log*n)，直到 2019 年，終於證明了 Schönhage 與 Strassen 的猜測 O(n log n)。

Volker Strassen 的大矩陣乘法

值得一提的是，Volker Strassen 除了是「大整數乘法」的始祖外，他也是「大矩陣乘法」的始祖（筆者寫到這裡，不自覺的跪了下來）。以 2×2 的矩陣來說，傳統計算

時，由於 x = ae + bg, y = af + bh, z=ce + dg, w=cf+dh，總共需要 8 次的乘法，但 1969 年，Strassen說，先計算下面 7 個值，

然後讀者可以自行驗證

因此只用了 7 個乘法就完成了。天啊！這是怎麼想到的！

一般 n×n 矩陣乘法，用 Strassen algorithm 只需要 O(n^log7) = O(n^2.8) 次乘法。從此大家才知道，原來矩陣乘法竟然可以比 n³ 還要快，矩陣乘法的改進也有相當精彩的發展歷史，詳細就不再一一介紹了，目前最好的結果是 2014 年 François Le Gall 的 O(n^2.3728639)。

演算法已經超越所需要的計算尺度啦

不管是大整數乘法，或大矩陣乘法，目前都是以 Schönhage–Strassen algorithm 與 Strassen algorithm 為主流，沒有採用後來看起來較好的方法主因是後來的方法太複雜，且要在很大很大很大的整數、矩陣執行效能才會比較好，已經超越了人類目前所需要的計算尺度。另一方面，電腦硬體的發展快速，會直接把這些演算法寫到晶片，變成指令集，讓程式直接呼叫，甚至是多條相同的指令可以平行處理，經由硬體的加速，乘法的速度已經超越了演算法改進的速度了（尤其是矩陣的乘法）。

不過只要還沒達到所謂的最佳解，相信數學家們都還是會繼續為數學理論極限而努力。

參考文獻

• Schönhage and V. Strassen. Schnelle Multiplikation großer Zahlen. Computing, 7:281–292, 1971.
• Fürer. Faster integer multiplication. In Proceedings of the Thirty-Ninth ACM Symposium on Theory of Computing, STOC 2007, pages 57–66, New York, NY, USA, 2007. ACM Press.
• David Harvey, Joris Van Der Hoeven. Integer multiplication in time O(n log n). 2019. hal-02070778

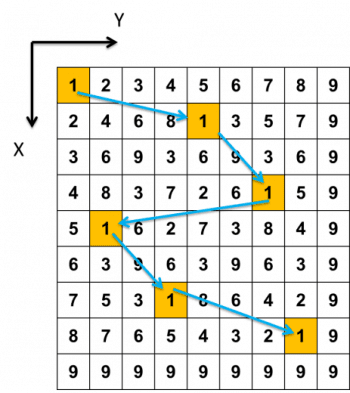
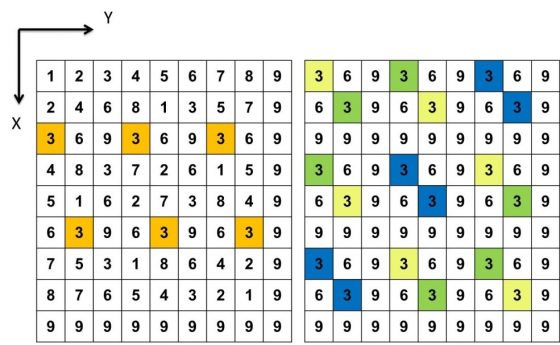
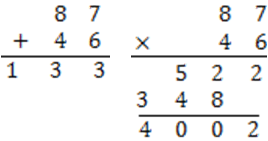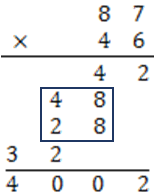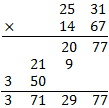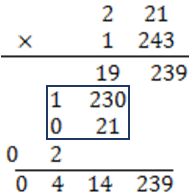我們從小學二年級就開始學習九九乘法表，但是上大學以後大家就開始正大光明地使用計算機，九九乘法表和心算能力就只剩下買東西的時候算錢可以比較快，那小時候學心算到底要做什麼呢？沒法馬上回答只好先來轉移一下話題，九九乘法表其實沒有你想像的那麼簡單，裡面有著你不知道的數學奧秘，且讓我們繼續看下去。

算過生命靈數就懂的數學：位數根

不知道大家還記不記得，以前在檢查一個正整數是不是 3 或 9 的倍數，我們會將正整數的每個位數數字相加，看加總的數字是不是 3 或 9 的倍數來判斷。或者大家可能也算過號稱可解析命格的「生命靈數」，將自己的出生年月日中每個數字加總，超過 9 就再重覆這個計算過程，直到加到不能在加之後得出一個屬於自己的「生命靈數」。這樣的作法其實你已經運用了一個正整數的性質——「位數根」。

到底什麼是位數根？它可以叫做數根、數字根，英文是 digital root 或 digit sum，就是把一個正整數各個位數的數字加總，若其和大於 9，則再將所得數的數字再加總一次，如此反覆這個步驟直到所得新數介於 1 至 9之間，稱此新數為原數的位數根。在此 D (n) 表示整數 n 的位數根，例如：9527 的位數根運算為 D (9527) = D (9+5+2+7) = D (23) = D (2+3) = D (5) = 5，5 即為 9527 的位數根。

如果用位數根來看九九乘法表…

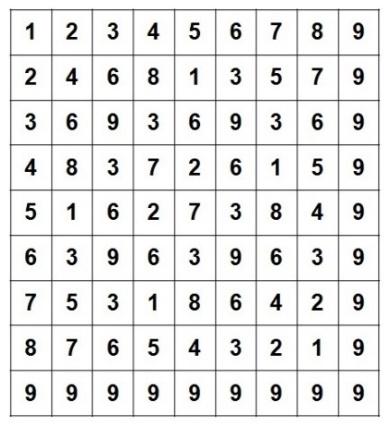
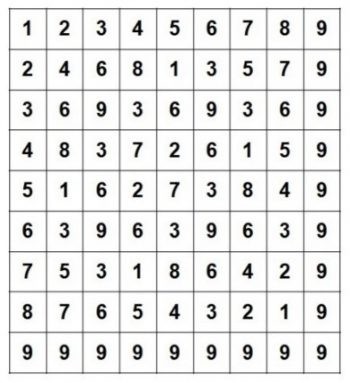
講了這麼多，數學奧秘到底在哪？先來看一下下圖的九九乘法表吧！不過，這個表和我們小時候背的不太一樣，它是一個 9×9 的表格，裡頭的數字是上方第一列的數字與左方第一欄的數字相乘的結果。

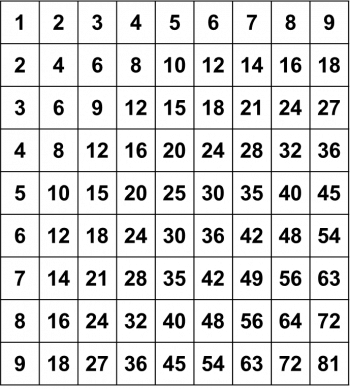
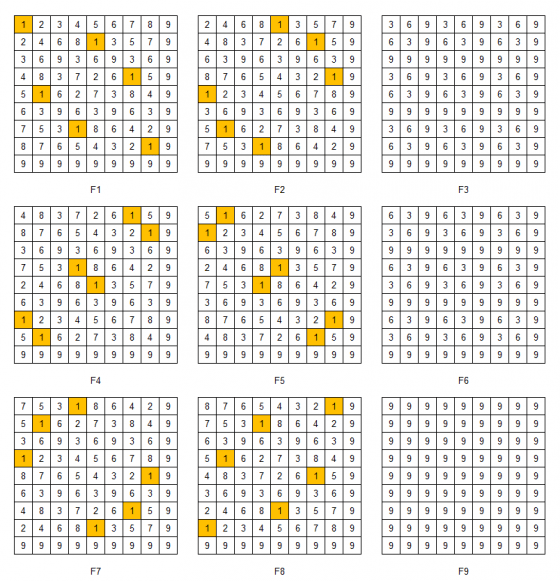
如果把這個九九乘法表的每一個數字都進行位數根運算，會出現什麼樣的結果？你可以自己試試看，也可以直接看圖 2 的結果。

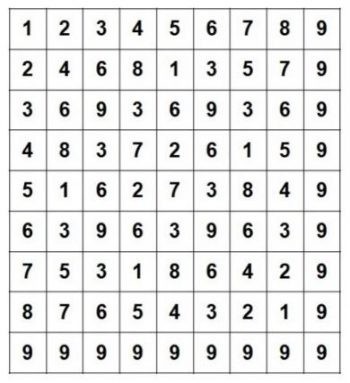
經過位數根運算後，九九乘法表就轉換成了著名的「吠陀方形」（Vedic square）。Vedic 這個英文字是從印度文 Vedas 來的，中文翻譯的「吠陀」常讓人聯想到精油或瑜珈，但在古印度文中它的意思是知識，所以可以把吠陀方形想像成是一個帶有知識的正方形。嗯？怎麼聽起來很像《平面國》這本書的故事情節呢 [1]。

《平面國》的主角是一位活在平面國的正方形男性，在一個偶然的機會下，一位「球體天使」帶他「向上」離開了平面國並遊歷了立體國，使得他成為最具知識的一號人物。回到平面國以後，主角迫不及待地想告訴大家「向上，而非向北」的體驗與真理，但先知總是孤獨的，平面國的人民會相信一個自稱掌握立體知識的正方形嗎？

吠陀方形可能早在佛陀之前就出現了

話說吠陀方形被發現的確切年代已經不可考，只知道數個世紀之前北印度的人們就已充分了解吠陀方形的性質，屬於古印度數學 [2]。古印度歷史有段時間叫做吠陀時期（Vedic period），大約是西元前 1500 年至西元前 500 年。如果說吠陀方形是在吠陀時期被發現的，那就是佛陀的年代甚至更早以前，真的很深很遠很古典哎。

吠陀方形後來也影響了伊斯蘭文化，西元 770 年時穆斯林將吠陀方形併入他們的數學知識體系中。事實上早期伊斯蘭文化的數學知識是比西方還要先進的，而且當時無論在技術與哲學上都非常強盛。伊斯蘭世界的數學到底有多厲害呢，可以從傳統伊斯蘭幾何圖樣（Islamic pattern）的藝術性裝飾看見，例如西班牙的阿罕布拉宮。由於可蘭經禁止具象化的偶像崇拜，因此伊斯蘭藝術中並沒有描繪人或是動物的圖畫，而是運用大量對稱且看似繁複的幾何圖樣，這些圖樣有專文與專書探討 [3,4]。

吠陀方形中藏著秘密圖形

吠陀方形與位數根胚騰（digital root patterns）密不可分，胚騰又是個什麼東西？胚騰就是 pattern，可以代表圖樣、規律、模式，甚至是一切有跡可循的事物 [5]。而數學是一種胚騰的科學（the science of pattern），尤其是在現今資料科學蓬勃發展的時代尋找胚騰與關聯更是重要無比，單單數字計算並不是數學。從未知中探究與發現規律與胚騰，是數學研究中最讓人目眩神迷的地方，位數根的研究與發現正屬於這類的驚奇。

講了這些少為人知的歷史和名詞以後讓我們再次回到圖 2，裡頭也有許多隱藏的圖樣，建議讀到這裡先暫停花幾分鐘觀察一下吠陀方形，避免破壞大家的樂趣。

好，剛剛提到的位數根胚騰呢？那是由位數根所在的位置組成的胚騰，意思是說，代數和幾何扯上關係了！

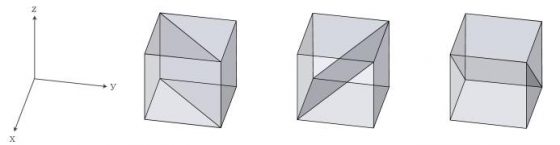
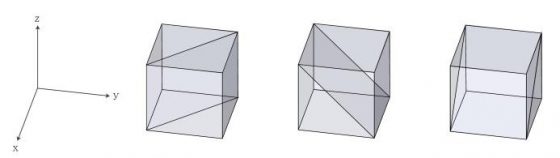
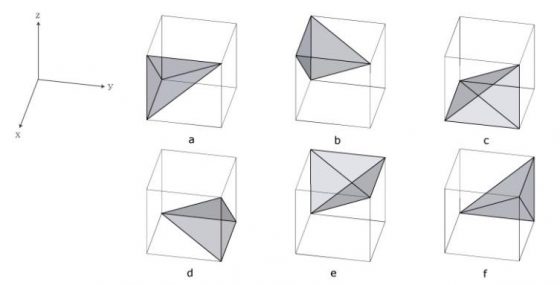
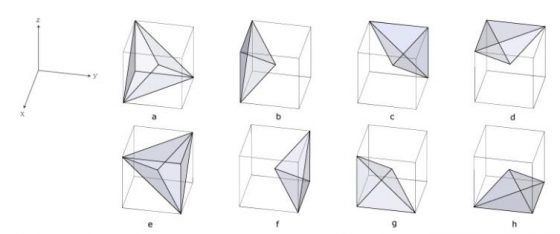
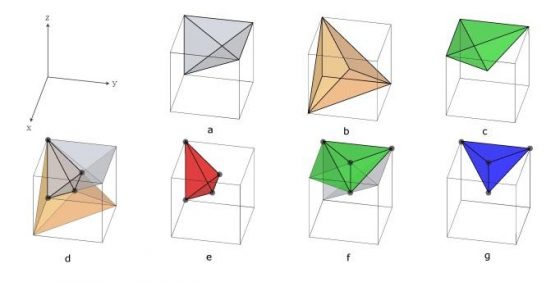
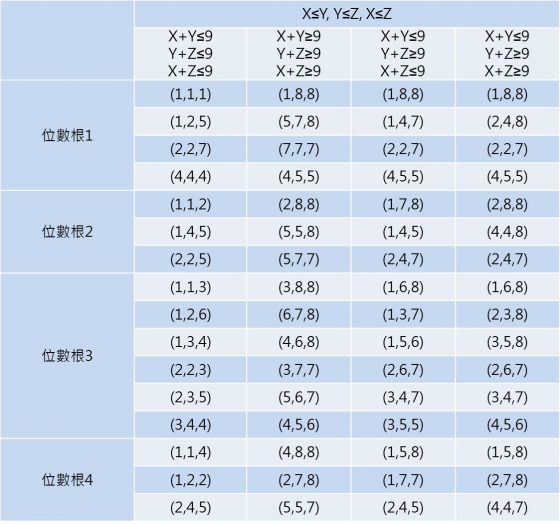
吠陀方形的行列數字組成與特定數字構成的胚騰，有著許多對稱性與互補性。位數根的分布也呈現有趣的幾何圖樣。下面的圖3中 D1 至 D9 分別為位數根 1 至 9 在吠陀方形中構成的圖樣 [6]，裡面的圖樣看起來有六邊形、長方形，還有多邊形等。

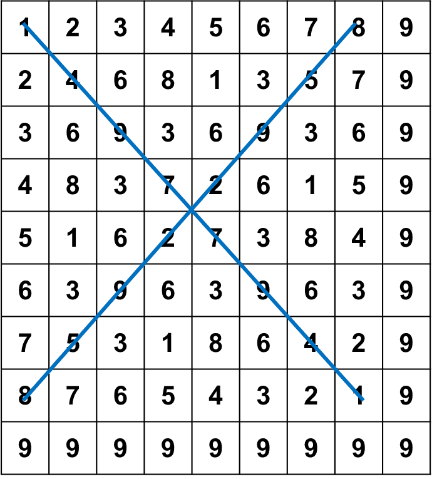
若是構成兩個圖樣的位數根總和為 9，這兩個圖樣將沿著鉛直線相互鏡射。像是數字 1 與數字 8 的位置構成的幾何圖案，是沿著鉛直線鏡射對稱的，或者是旋轉 90 度也可以得到。而數字 2 與數字 7、數字 3 與數字 6、數字 4 與數字 5 為另外三組以數字構成的對稱圖樣，由此可見數字 9 在位數根的世界中是個重要的數字，有發現一個整數加了 9 的倍數以後位數根不變嗎？數字 9 的胚騰比較特別，沒有和其他的數字構成互補圖樣自成一個世界，所以就暫時先不探討它。

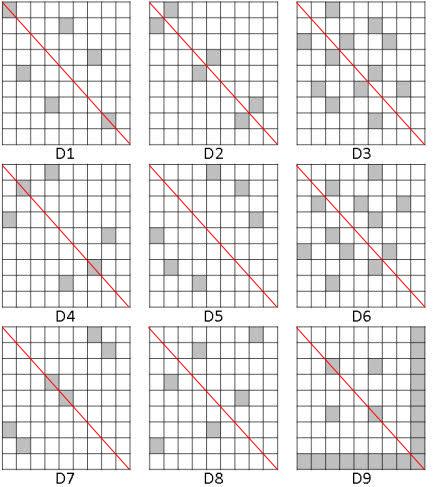
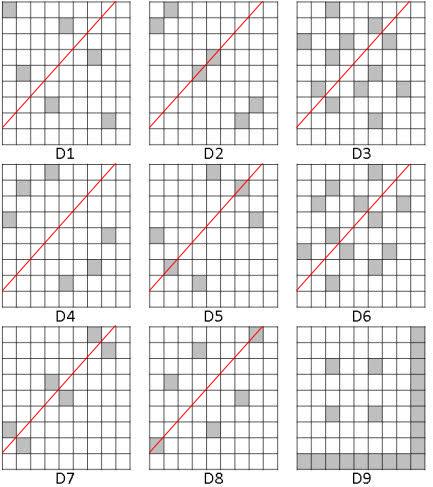
仔細觀察一下會發現 D1 至 D8 這 8 個胚騰有兩條對稱軸，其中一條是 X=Y，另一條是 X+Y=9，他們的交點是 (4.5, 4.5)。裡面的點都會照著這兩條對稱軸相互對稱與鏡射，可以從代數上解釋，也可以直接看圖找規律。X=Y 這條對稱軸代表的意思是一個座標點 (X,Y) 的 X、Y 值可以互換變成 (Y, X)，其位數根不變，像是 (4,7) 和 (7,4) 的位數根都是 1。X+Y=9 這條對稱軸可以藉由 (X,Y) 這個點找到 (9-Y, 9-X) 這個點，也就是可以從 (4,7) 找到 (2,5) 這個點，如此一來就可以用少數的座標點找到其他點簡化問題。

沒想到小時候背的九九乘法表，居然藏著這麼多數學奧秘！數千年前的位數根胚騰和吠陀方形，讓世界為之瘋狂稱為 Magic。

• 此文作者本系列文章獲得臺北市政府文化局藝文補助

參考資料

1. 愛德溫．A．艾勃特，平面國：向上，而非向北！，新北市：魔酒出版，2014
2. Jones, L. “Mathematics and Islamic art”, Mathematics in School, 18(4), 32–35, 1989.
3. 塞伊德．蔣．阿巴斯和阿默．夏克爾．薩爾曼，伊斯蘭的幾何藝術，台北縣新店市：左岸文化，2004。
4. Lu, P. J., Steinhardt, P. J. “Decagonal and Quasi-Crystalline Tilings in Medieval Islamic Architecture”, Science, 315(5815), 1106–1110, 2007.
5. 曹亮吉，從生活學數學(第二版)，臺北市：遠見出版，2009。
6. Lin, C. Y. Digital Root Patterns of Three-Dimensional Space. Recreational Mathematics Magazine, 3(5), 9–31, 2016.

到目前為止，吠陀立方系列文章已經介紹過流傳千年的古印度數學－吠陀方形（Vedic square），我運用數字感把它加上一個維度定義了吠陀立方（Vedic cube），再以樓層法去解析位數根胚騰（Digital root patterns）層層之間的關係[1]，這回來介紹吠陀立方對稱面法。

吠陀立方：將吠陀方形從平面延伸成立體

吠陀方形就是將大家熟悉的九九乘法表中每一個數字進行位數根（digital root）運算，例如說 4 乘上 8 會得到 32，把  3 加上 2 得到 5，這個 5 即為 32 的位數根，也是吠陀方形裡座標點（4, 8）的數值。吠陀方形在西元 770 年被穆斯林納入伊斯蘭文化的數學知識體系之中[2]。

其中位數根所在的位置互相連結後組成的胚騰（pattern）構成了特定的幾何圖案如下圖：

吠陀立方則是將吠陀方形從平面延伸成立體，也就是三個數字相乘的三維乘法表（9×9×9），是整個立方體中各個座標點的數字進行位數根運算後的結果，可以用函數 D(X, Y, Z) 代表吠陀立方中座標 (X, Y, Z) 該數字的位數根，實際運算時的數學式為 D(X×Y×Z)。例如座標點 (2, 4, 7)在吠陀立方中的數值即為 D(2×4×7) = D(56) = D(11) = D(2) = 2。

之前提到以程式繪出吠陀立方中的位數根胚騰，其散布情況相當複雜（可見此篇），難以看出這些座標點在空間中構成的意義。用樓層法解析吠陀立方，能夠觀察出位數根胚騰在各層本身的性質，甚至可從二維的吠陀方形推算不同樓層之間的變換。只是樓層法是把三維空間轉化成許多二維平面，較少探討位數根胚騰在三維空間中彼此的相關性，這時又該如何是好呢？

解構吠陀立方

回到數學或科學研究的基本方法，觀察、觀察、再觀察。

吠陀方形中，位數根 1 至位數根 8 位置構成的八個圖樣會沿著兩條對角線 X=Y 與 X+Y=9 對稱，兩條對角線為對稱軸，不僅在 X-Y 平面可以成立，在 Y-Z 平面、X-Z 平面同樣成立。從二維拓展至三維的過程中，對角線就變成了對角面同時也是對稱面，因此吠陀立方共有六個對稱面。

為了找到空間中最小不可分割的塊體，也就是不重複的基本元素（element），以及內部對應的座標點，希望能探討位數根胚騰在三維空間中的關係，所以我將沿著對稱面群切割與解構吠陀立方。

吠陀立方的對稱面群分為兩組，一組叫做主對稱面群（main symmetry planes, MSP），為 X=Y, Y=Z, X=Z，這三個對稱面都有通過原點，如圖 4；另一組則為副對稱面群（secondary symmetry planes, SSP），為 X+Y=9, Y+Z=9, X+Z=9，如圖 5。

圖 4 和圖 5 的每一塊灰色塊體，都可藉由一次鏡射後得到完整的吠陀立方。至於分析的塊體取對稱面群兩邊任何一塊皆可，並沒有限制要取對稱面群的哪一邊。除此之外，可以選擇先在 X-Y, Y-Z, X-Z 平面沿著主副對稱面群切割，得到的塊體將是三角柱體，其底面為 1/4 正方形面積的等腰直角三角形。

沿著主對稱面群分割吠陀立方的結果如圖 6，得到 6 個 MSP 四面體（MSP unit tetrahedron），值得注意的是這 6 個四面體為雙直角四面體（birectangular tetrahedron），顧名思義此四面體包含兩個直角，在數學上也稱為 Schläfli orthoscheme。此雙直角四面體的底面為 1/2 正方形面積的等腰直角三角形，高為立方體的邊長，因此體積為吠陀立方的1/6。

每一個 MSP 四面體可沿著 X=Y, Y=Z, X=Z 共鏡射三次得到吠陀立方。主對稱面群的交集為一條線，也就是吠陀立方的對角線 X=Y=Z，因此會將吠陀立方分成 6 塊。

副對稱面群分割後的結果為 8 個塊體如圖 7，包括 2 個 SSP 六面體（SSP unit hexahedron），體積各佔吠陀立方的 1/4；以及 6 個 SSP 四面體（SSP unit tetrahedron），其底面為 1/2 正方形面積的等腰直角三角形，高為吠陀立方邊長的 1/2，體積各佔吠陀立方的 1/12。副對稱面群的交集為一個點，為吠陀立方的中心 (4.5, 4.5, 4.5)，因此會將立方體分成 8 塊，而這 8 塊的體積並不完全相同。

把幾何問題從書桌搬到餐桌！

在思考副對稱面群分割問題時，為了驗證自己的想法，在愛爾蘭的聖誕假期，我把所有的研究材料從書桌搬到了餐桌，以做菜來輔助研究，餓的話馬上補充體力。

平常雖然沒有那麼喜歡豆腐，但豆腐不僅好切、還能增進空間幾何的思考，更可以照顧到五臟廟，在廚房實作數學效果意外倍增！老實說，這麼可愛的幾何豆腐還真讓人有點捨不得吃掉呢。

切完豆腐和著其他食材煮湯飽食一頓以後，問題也快解完了。最後的步驟是沿著另一個對稱面群繼續分割，即使副對稱面群分割出的塊體並不全然相同，但最終結果為一單位四面體，其底面為 1/4 正方形面積的等腰直角三角形，高為立方體邊長的 1/2，體積各佔吠陀立方的 1/24，如圖 9。

原先主對稱面群分割的 MSP 四面體（1/6 立方體體積）會被副對稱面群的邊界條件分為形狀相等的 4 小塊；而副對稱面群分割出的塊體則有二種情況，第一種為 SSP 六面體（1/4 立方體體積）將會被主對稱面群的邊界條件分為形狀相等的 6 小塊，第二種情況則是 SSP 四面體（1/12 立方體體積）將被分為形狀相等的 2 小塊。

無論由主對稱面群或是從副對稱面群開始分割，得到的結果相同，為 24 塊全等的四面體如圖 10，稱之為吠陀立方單位四面體（unit tetrahedron of Vedic cube, UTVC），為三直角四面體（trirectangular tetrahedron），表示其中一個頂角包含三個直角。任一個 UTVC 已是最小不重複的基本元素，可沿著對稱面群鏡射六次得到原先的吠陀立方。

也就是說，我們只要列出 UTVC 裡面的位數根 1、2、3、4 座標點位（可藉由旋轉分別得到位數根 8、7、6、5，如吠陀方形的位數根胚騰），就可以將原先複雜的座標點位分布，簡化成不能再簡化的胚騰。

表1列出了位數根 1、2、3、4 在 4 個 UTVC 中的座標點位。表中的點包含了邊界條件上的點，這些點會被數個 UTVC 同時共用。UTVC 中的位數根座標點沿著對稱面群確實能鏡射出其他位數根座標點，而每個 UTVC 中座標點構成的向量也相同。

• 表1｜位數根 1、2、3、4 在 4 個 UTVC 中的座標點。

從二維平面至三維空間，吠陀立方的更多應用

吠陀立方的發展是從二維平面至三維空間，其簡化是了解三維空間的位數根胚騰性質的重要步驟。從對稱面群解構的方法可大幅簡化吠陀立方的複雜度，也可找出三維空間的基本元素，不再限於吠陀方形於二維平面隱含的圖樣與規律（樓層法）。

位數根於吠陀立方散布的胚騰，是大自然本身形成的奧妙形態，除了純數學研究或是建構演算規則外，也許能和分子晶體、空間、藝術或是建築等相關領域結合應用。像是行為藝術教母瑪莉娜·阿布拉莫維奇（Marina Abramović）與她的夥伴曾在Nightsea Crossing的作品中，根據吠陀方形而決定各自所穿的衣服顏色。

吠陀立方是受到古印度數學吠陀方形、伊斯蘭幾何圖樣、倫敦蛇形藝廊 2002 的啟發，跨越數千年與東西方文化最終在台灣這個文化交融之地產生的數學。我身為吠陀立方的發明與發現者，特別期待未來有人能受到啟發，將吠陀立方的概念運用於建築設計或藝術創作，就像是塞西爾．巴爾蒙德（Cecil Balmond）運用演算法把正方形轉化成蛇形藝廊 2002 那樣令人驚艷。

對我來說，數學與藝術是兩面鏡子，可以一直相互映射彼此的光亮；而東方和西方，也能夠不斷跨越邊界彼此對話與啟發。

後續，我們再來聊聊如何將吠陀立方轉化成數學藝術創作。

參考資料

1. Lin, C. Y. Digital Root Patterns of Three-Dimensional Space. Recreational Mathematics Magazine, 3(5), 9–31, 2016.
2. Jones, L. “Mathematics and Islamic art”, Mathematics in School, 18(4), 32–35, 1989.