- 文/郭君逸 │國立臺灣師範大學數學系副教授
編按:說到乘法,我們很快都會想到國小的共同回憶「九九乘法表」。背誦它對我們來說可能是一位數相乘最快的解方,多位數我們就用直式乘法運算。但如果是超超超超超超超級多位數互相相乘呢?有沒有更快的方法?
對於人腦來說可能大位數的乘法已經沒有意義,但對於電腦來說,有新的乘法方式可是大大的不一樣!三月時有數學家發表了有史以來將大數字相乘最快的新乘法方式,讓我們一起來一探究竟吧!
從「九九加法表」與「九九乘法表」談起
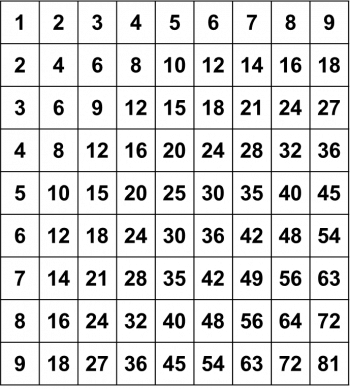
我們在國小時的數學,一開始就會先學「數數」,要會數 1、2、3、⋯接下來才能學加法,例如:8+5 就是 8 往後數 5 個…9, 10, 11, 12, 13,所以 8+5=13。但每次都這樣做建構式的加法太慢,成不了大事,於是大家就背了「九九加法表」(雖然老師沒提這個表,但事實上大家的確都背了!)來快速處理一位數的加法,後來再學直式加法搭配進位,就能夠計算多位數的加法。

學習乘法也是差不多的歷程。正整數的乘法其實本質就是「重複做很多次加法」,例如 6 × 4 其實就等於 6+6+6+6 或是 4+4+4+4+4+4,但很快地我們馬上就會發現這樣做建構式的乘法,速度太慢,成不了大事,於是大家就背了「九九乘法表」來快速處理一位數的乘法,然後再學直式乘法搭配進位,來處理多位數的乘法。
加法跟乘法我們都可以做到高位數,但究竟是加法比較快,還是乘法較快呢?

到底要算幾次?加法與乘法運算次數比較
若是一位數對一位數的話,當然是一樣快,因為「九九加法表」跟「九九乘法表」我們都倒背如流了;但當「2 位數加 2 位數」與「2 位數乘 2 位數」來比呢?
明顯乘法的運算次數一定比加法多,光直式乘法最後的 522+3480 就超越了 87+46 的加法數,何況還要做 7×6, 8×6, 7×4, 8×4 四次乘法;然後 7×6 與 8×6 也要做一個加法才能算出 522,7×4 與 8×4 也一樣。
一般來說 n 位數加 n 位數,連進位都算進去的話,要做 2n-1 次一位數加法;但 n 位數乘 n 位數的話,最多會用到 2n(n-1)的一位數加法,與 n2 次的一位數乘法。可見,乘法的運算次數是隨著位數的平方成長,所以計算乘法比較慢。

Karatsuba以加減法取代乘法,加快運算速度?
1960年,俄羅斯的大數學家 Andrey Kolmogorov 在一次研究討論中提出他的猜測(n 位數的乘法必須用到至少 n2 數量級的一位數乘法),例如 2 位數乘以 2 位數必須進行 4 次一位數乘法,他認為不能再快了。
結果一個禮拜後他的學生 Anatoly Karatsuba 就推翻這項猜測,找到僅需 3 次一位數乘法的計算。以 87×46 為例,Karatsuba 的方法是這樣的,先算十位相乘 8×4=32,與個位相乘 7×6=42,這個部份與傳統直式乘法一樣,但他卻只用了一次乘法就算出了 8×6和 7×4 且同時把它們加起來。我們先把傳統直式乘法改成如下:
中間的方框就是要計算 8×6 加 7×4,Karatsuba巧妙的用 (8+7)×(4+6)- 8×4-7×6 來達到同樣的效果。注意到,上式中只有第一個乘號要算,後兩個剛剛已經算過了,也就是說 Karatsuba 用一個加法與兩個減法取代了一個乘法。讀者這時可能會想說,拿一個一位數乘法去換三個加減法,又不是頭殼壞去,這樣不是反而慢嗎?
我們來看一下 4 位數的情況, 2531×1467 一樣先算 25×14 與 31×67,然後中間的 25×67+31×14 用 (25+31)×(14+67)-25×14-31×67 計算,最後加總起來。
如同前面的分析,此處一樣用到三個二位數乘法,而每個二位數乘法又用到三個一位數乘法,所以總共用到 3×3 =9 次一位數乘法。因此一般 n 位數的乘法,用這種技巧,可以只用到
3log2 n=nlog2 3=n1.58
個一位數乘法。位數越高,用到的一位數乘法數就會越接近 n1.58 的常數倍。對於人來說,因為把一個乘法換三個加減法,並沒有比較快,何況還要遞迴的操作;但是,對電腦而言就不是這樣了。

電腦運算的本質:二進位
電腦的本質上是二進位的系統 (哪有!我用電腦這麼多年,沒看到什麼二進位啊!那是現在電腦發展很快,事實上隨便顯示一張小圖、或一個字,背後都做了數百萬次的二進位運算。)而電腦的加法是用位元的邏輯運算來達成(也就是 AND、OR、XOR、NOT、Shift 這些東西來組成的),而位元邏輯運算超快,詳細我們就不說了,總之電腦的加法非常快。
那電腦的乘法,真的是用 Karatsuba 的方法嗎?其實也不是,我們先來看一下 8 位元的電腦怎麼做乘法好了。以 11 乘以 14 來說,化成二進位變成 00001011 與 00001110 (前面要補 0,因為 8 位元的電腦它就是用 8 個位元儲存數字。)
這不就是直式乘法嗎?這樣哪有比較快?有的。因為人類習慣十進位,所以要背「九九乘法表」;電腦用的是二進位,所以要背「一一乘法表」!!沒錯,所以等於不用背,二進位的直式乘法,其實只是被乘數的平移,然後加起來而已,換句話說,其實乘法,也是一堆位元邏輯運算而已,所以也是超快的。
那 Karatsuba 的方法用在哪呢?用在很大很大的數字相乘的時候。電腦的乘法雖快,但 8 位元電腦,最大就只能處理 2⁸-1=255 以內的乘法,乘完後超過 255 的話就不能處理了,16位元電腦最大可以處理到 65535 以內的數,而現在的64位元電腦就可以處理到……一個非常大的數,呵呵。
那超過電腦能處理的數的話,到頭來,還是要用傳統的方法來處理,為了不要讓數字太大,我們以 8 位元的電腦為例,處理數字就會看成 256 進位來處理,533×499 就會變成
所以當數字大的時候,這時 Karatsuba 的方法就有用了。
值得一提的是,當電腦硬體從 8 位元升級到 16 位元時,軟體若沒有改成 65536 進位的話,而用 16 位元電腦來存 255 以內的數,前面就會補了更多的 0,處理起反而會浪費時間。而若軟體有跟著處理成 65536 進位的話,533×499 就會變只有位元邏輯運算而已,會超快。這就是為什麼電腦硬體剛進入 64 位元時代時,軟體沒有跟上的話,執行程式反而變慢的原因。
歷經三十年的演算法改進
OK,我們再回來乘法的問題。Karatsuba 的方法,在數字大的時候的確可以加快乘法,以一千位數的乘法來說,此法的速度大約是傳統乘法的 17 倍。
隔年,1963 年,A. L. Toom改進到了 ;後來 1966 年 Arnold Schönhage 用了新的方法推進到
;1969 年 Knuth(沒錯,就大家所知道的Knuth),改進到
。
後來 1971 年,Schönhage 捲土重來,與 Volker Strassen 利用快速傅立葉變換改進為 O(nlogn log logn),此為有名的 Schönhage–Strassen algorithm,在差不多三萬位數以上的乘法,會比 Karatsuba 方法還要快。此法也是目前大數字乘法的主流,著名的梅森質數搜尋網(Great Internet Mersenne Prime Search,在 2018 年 12 月找到第 51 個)就是用 Schönhage–Strassen algorithm 來達到快速乘法。
隔了三十幾年,一直到了2007年,Martin Fürer一樣是用快速傅立葉變換,將複雜度下降到了O(n (log n) 16log*n),其中 log*n 就是 n 取幾次 log 會讓這個數小於 1,這是一個成長很慢的函數,基本上可以視它為常數了。
最後最後,David Harvey 與 Joris Van Der Hoeven 寫了幾篇的論文,把這個結果改成 O(n(logn)8log*n),然後 O(n(log n)4log*n),直到 2019 年,終於證明了 Schönhage 與 Strassen 的猜測 O(n log n)。
Volker Strassen 的大矩陣乘法
值得一提的是,Volker Strassen 除了是「大整數乘法」的始祖外,他也是「大矩陣乘法」的始祖(筆者寫到這裡,不自覺的跪了下來)。以 2×2 的矩陣來說,傳統計算
時,由於 x = ae + bg, y = af + bh, z=ce + dg, w=cf+dh,總共需要 8 次的乘法,但 1969 年,Strassen說,先計算下面 7 個值,
然後讀者可以自行驗證
因此只用了 7 個乘法就完成了。天啊!這是怎麼想到的!
一般 n×n 矩陣乘法,用 Strassen algorithm 只需要 O(nlog7) = O(n2.8) 次乘法。從此大家才知道,原來矩陣乘法竟然可以比 n³ 還要快,矩陣乘法的改進也有相當精彩的發展歷史,詳細就不再一一介紹了,目前最好的結果是 2014 年 François Le Gall 的 O(n2.3728639)。
演算法已經超越所需要的計算尺度啦
不管是大整數乘法,或大矩陣乘法,目前都是以 Schönhage–Strassen algorithm 與 Strassen algorithm 為主流,沒有採用後來看起來較好的方法主因是後來的方法太複雜,且要在很大很大很大的整數、矩陣執行效能才會比較好,已經超越了人類目前所需要的計算尺度。另一方面,電腦硬體的發展快速,會直接把這些演算法寫到晶片,變成指令集,讓程式直接呼叫,甚至是多條相同的指令可以平行處理,經由硬體的加速,乘法的速度已經超越了演算法改進的速度了(尤其是矩陣的乘法)。
不過只要還沒達到所謂的最佳解,相信數學家們都還是會繼續為數學理論極限而努力。
參考文獻
- Schönhage and V. Strassen. Schnelle Multiplikation großer Zahlen. Computing, 7:281–292, 1971.
- Fürer. Faster integer multiplication. In Proceedings of the Thirty-Ninth ACM Symposium on Theory of Computing, STOC 2007, pages 57–66, New York, NY, USA, 2007. ACM Press.
- David Harvey, Joris Van Der Hoeven. Integer multiplication in time O(n log n). 2019. hal-02070778


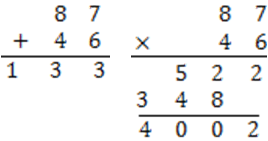
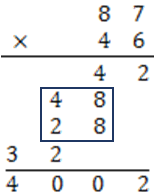
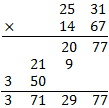

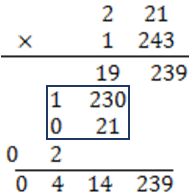

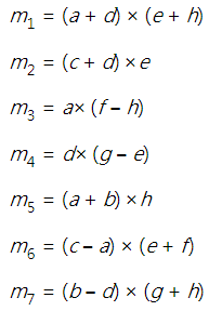
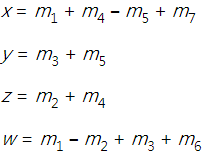






























![吠陀方形中的位數根胚騰[6]](http://pansci.asia/wp-content/uploads/2016/12/eccbc87e4b5ce2fe28308fd9f2a7baf3-1.jpg)