「數感盃青少年寫作競賽」提供國中、高中職學生在培養數學素養後,一個絕佳的發揮舞台。本競賽鼓勵學生跨領域學習,運用數學知識,培養及展現邏輯思考與文字撰寫的能力,盼提升臺灣青少年科普寫作的風氣以及對數學的興趣。
本文為 2019數感盃青少年寫作競賽 / 高中職組專題報導類佳作之作品,為盡量完整呈現學生之作品樣貌,本文除首圖及標點符號、錯字之外並未進行其他大幅度編修。
- 作者:李元萌、 施宥旭/國立臺南二中。

一、研究動機
古代詩人常因主觀心情的劇變,使得客觀時間或空間的描述產生放大或縮小的意象,用以類比其喜怒哀樂的轉折。「朝辭白帝彩雲間,千里江陵一日還」,即因李白獲赦後喜悅至極,而感覺時間變短;「劉郎已恨蓬山遠,更隔蓬山一萬重」,乃因詩人在送別友人時,對其日後的旅途而感覺距離的拉長;「似將海水添宮漏,共滴長門一夜長」則描寫女子因思念之情而對夜晚感覺格外漫長。
在高中國文〈師說〉一課中認識韓愈,藉由欣賞詩詞更讓我們了解他人生中的挫折與難關,在〈瀧吏〉、〈食曲河驛〉、〈武關西逢配流吐蕃〉、〈過始興江口感懷〉⋯⋯等詩中,皆描繪其貶謫途中之感,尤在〈左遷至藍關示侄孫湘〉中,刻劃其剛被貶謫的抑鬱之情, 我們也對詩中空間與時間的真實度感到好奇,遂以其生平與貶謫途中的地理位置,深入探討並進行研究。我們將從幾首詩中提及關鍵的數字,進行研究並分析其空間、時間的真實性:
- 韓愈的貶謫路途十分遙遠,〈左遷至藍關示侄孫湘〉中「一封朝奏九重天,夕貶潮州路八千」 一句,不禁讓人想一探是否真如詩中所寫從長安城到潮州長達八千里呢?
- 韓愈是否真能在一日之間到達這潮濕蒸鬱,暗無天日的潮州呢?「我今罪重無歸望,直去長安路八千。」韓愈在〈武關西逢配流吐蕃〉中亦提及「路八千」, 這樣的關聯是與上首詩巧合嗎?
- 〈瀧吏〉一詩中「下此三千里,有州始名潮。」究竟是否自昌樂瀧至潮州真要三千里呢?
二、故事背景
貶謫文化讓中國文學史更添色彩,作家余秋雨在《文化苦旅》一書中認為:「詩人被貶到外頭,失了寵,摔了跤,只好與山水親熱,這樣一來,文章有了,詩詞也有了,而且往往寫的不錯。」也因為貶謫路途的遙遠,跋山涉水,所到之處無不是蠻荒之地,生活極其困頓, 憂憤之下才能寫出流傳千古的作品。
而名列唐宋古文八大家的韓愈亦是如此,元和十四年, 唐憲宗派使者往鳳翔迎佛骨進宮中,供奉三日後送寺。韓愈毅然決然上呈〈諫迎佛骨表〉, 內容提及歷代信佛的帝王大都「運祚不長」,要求將佛骨「投諸水火,永絕根本,斷天下之 疑,絕後代之惑」遂引起皇帝震怒;但在崔群及國戚貴人為他說情之下,改貶潮州刺史。潮州位於廣東沿海,唐朝時尚未開發,韓愈長途跋涉,奔走任所,值藍關(今陝西省一帶)時逢大雪,人與馬早已疲倦,心中感到痛苦和絕望。還好其姪韓湘的勸慰,心情才稍為好轉, 寫下〈左遷至藍關示侄孫湘〉這首流傳千古的詩。
三、研究內容
路程的巨大數字,雖有可能使用誇飾筆法,但仍令人好奇,其實際的空間距離有多少? 需花費的時程多少?是否為刻意放大?
(一)距離的演算首先,我們以距離來探討韓愈這短艱苦的貶謫歲月。韓愈因〈諫迎佛骨表〉被貶,自唐代政治中心長安出發,依下列詩詞分析,陸續經過藍田關、武關西、曲河驛、楚昭王廟、昌樂瀧、 始興江及潮州市。
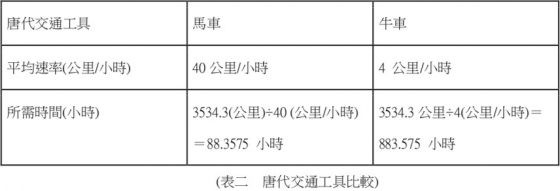
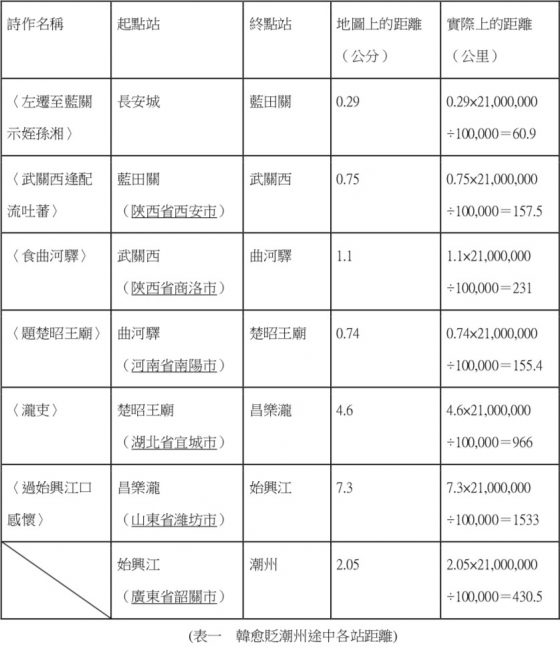
唐代以唐太宗李世民的雙步(左右腳各跨一步)為距離單位的標準,叫作「步」,並規定三百步為一里,一里為 454.2 公尺。一「步」的五分之一為一尺。唐代一尺相對於現在約 0.303 米,一里換算約 454.2 公尺。依照唐代古地圖所示,比例尺為 1:21,000,000,試計算各段路程的直線距離。(如表一)
【公式:地圖上的距離(公分)× 比例尺(1:21,000,000)÷100,000=實際上的距離(公里)】
1.〈左遷至藍關示姪孫湘〉
一封朝奏九重天,夕貶潮州路八千。欲為聖明除弊事,肯將衰朽惜殘年。
雲橫秦嶺家何在?雪擁藍關馬不前。知汝遠來應有意,好收吾骨瘴江邊。 本詩是在韓愈貶潮州時,自潮州出藍關時之作,可見其剛被貶謫時憂憤怨恨之心。由上 述資料得知,這段路程的總距離約為 3534.3 公里(=3534300 公尺),即 3534300 ÷ 454.2 = 7781.37 里,故韓愈在詩中所提及的八千里與實際距離相去不遠。
2.〈武關西逢配流吐蕃〉
嗟爾戎人莫慘然,湖南地近保生全。我今罪重無歸望,直去長安路八千。
此詩為韓愈謫潮州,途經武關西而作之。依唐朝古制,西邊所擒之蕃囚,皆會發配至南 方且不會被殺戮。而韓愈在南貶途中,自藍田入商洛於武關西時,遇到一群發配湖南的蕃囚, 感懷自己因言論不敬、冒犯帝王,被遠貶至瘴癘之鄉,覺得不如「蕃囚」,心情沉痛抑鬱,有感而作〈武關西逢配流吐蕃〉,也因為受到如此大的打擊,詩中才會用八千里一詞來說明自身的境遇。由上述資料可知,自武關西至潮州距離約 3315.9 公里(= 3315900 公尺),即 3315900 ÷ 454.2 = 7300.53 里,與詩中「直去長安路八千」相去不遠。
3.〈瀧吏〉
(節錄) 南行逾六旬,始下昌樂瀧。險惡不可狀,船石相舂撞。 下此三千里,有州始名潮。惡溪瘴毒聚,雷電常洶洶。 鱷魚大於船,牙眼怖殺儂。州南數十里,有海無天地。 潮州雖云遠,雖惡不可過。於身實已多,敢不持自賀。
韓愈赴潮州途中所作,聞潮州瘴癘之地,此種痛苦抑鬱的心情清楚呈現在此詩。 韓愈自昌樂瀧至潮州仍有約 1963.5 公里(= 1,963,500 公尺),即 1963500 ÷ 454.2 = 4322.98 里, 與其三千里之敘述有落差,推究原因可能是因連續六十天的「南行」,離長安愈來愈遠,驚怖之情愈增,故感覺離潮州十分接近。(二)時間的計算接著,我們利用幾項唐代的主要交通工具(馬車、牛車)計算其速率與時間,並檢驗合理性;再綜合現代的交通工具,討論如何才可使這八千里在半天內迅速抵達。
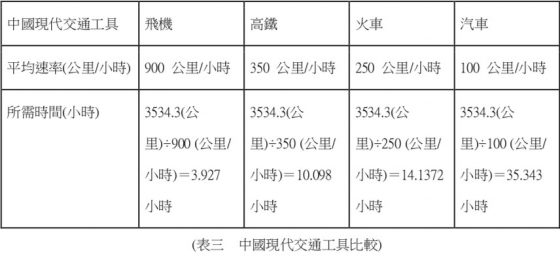
我們分析古代的交通工具,並計算出其速率與所需時間(如表二),由此得知,韓愈自長安城至潮州的這段路程至少需 3.5 天,故「一封朝奏九重天,夕貶潮州路八千」所描寫的時間是不合理的。再比較現代各種交通工具,並計算出其速率與所需時間(如表三)。
由此得知,韓愈若身處現代,應搭乘飛機或高鐵,才能如詩中所寫的在半天的時間內抵達潮州。
四、結論
韓愈在〈左遷至藍關示侄孫湘〉詩中,藉由「路八千」營造距離之遙以及「朝奏」、「夕貶」的用詞,刻劃出時間壓迫的侷促感;在〈武關西逢配流吐蕃〉詩中,韓愈以八千里之遙凸顯自身遭遇不如蕃囚,再加上是貶謫途中的第二站,故距離尚無誇大之詞;在〈瀧吏〉詩中因貶謫之途越來越接近潮州,憂憤之情油然而生,故恐懼感愈增,感覺離貶謫地潮州十分接近,距離因而縮短,感到迫促。
正如「朝為青雲士,暮作白首囚」(韓愈〈赴江陵途中寄贈王二十補闕李十一拾遺李二十六員外翰林三學士〉)所寫,韓愈真切敘述貶謫後的痛苦之情,字裡行間流露出憤恨之情,令人印象深刻。
再根據我們分析、驗算後,發現詩中對於空間(距離)的描寫並無誇大其詞,但在時間的描述明顯不符古代交通工具之性能。這也證明對客觀時間或空間的感受,常因作者當下主觀的生活際遇與心情,產生放大或縮小的情形,而這種變化也加深了文學的趣味性。