文/郭君逸|數學科普 Unimath 網站作者,國立台灣師範大學數學系助理教授、魔術方塊收藏家
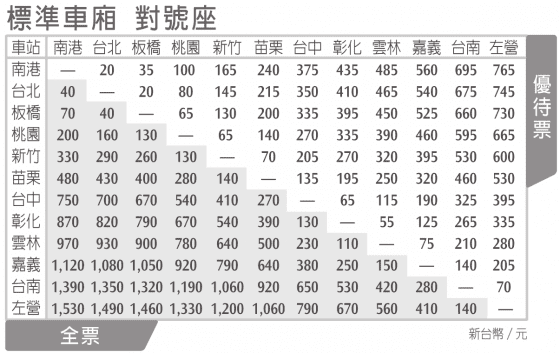
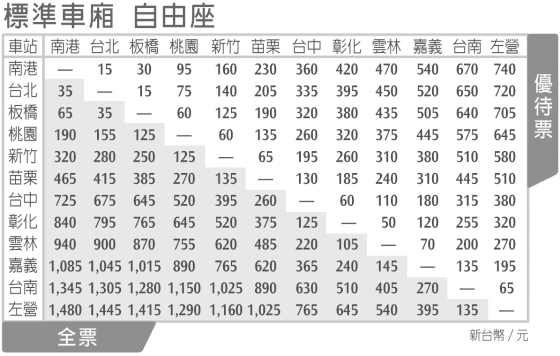
這是一張從高鐵網站下載的票價表。眼前除了一堆數字之外,你還注意到哪些數學呢?
「矩陣!」
對的,你的觀察很正確。矩陣是大學線性代數這門課裡的主角,線性代數和微積分兩者並列為一窺高等數學的計算基礎,因此除了自然科學領域的學生強迫必修,甚至一些社會科學領域的學生也需要修讀,例如經濟、商管······等。聽起來或許有點恐怖,不過別緊張,撇開複雜的計算,單純矩陣表示法其實是生活中蠻常見實用的技巧,可以做為一群事物中兩兩彼此之間的關聯表格。像是上圖高鐵票價關係就是「起」「訖」點間的票價關係,還有各種比賽中選手或球隊彼此間的勝負關係。
這張圖右上半部是半價的優待票,以下討論我們只要看左下半部的全票即可。不知道讀者有沒有發現,「彰化→左營」的票價原本是 670 元,但「彰化→嘉義 250 元」加上「嘉義→左營 410 元」卻是 660 元,分開買居然可以省 10 元!?
是不是一直把票分段買,就可以越來越便宜呢?
其實並非如此!
例如「嘉義→左營」是 410 元,但改成「嘉義→台南 + 台南→左營」兩段票的話,會變成 420 元,反而變貴了。
為什麼會有這種現象呢?

首先我們先來研究一下高鐵的票價訂法。政府每年會先用「消費者物價總指數(GICP)」來訂定每人的基本消費率,交通部把基本消費率乘以 1.2 當作高鐵的基本費率(2016 年)的基本費率是 4.386 元/人公里。(註:詳細計算方式請參閱:交通部高速鐵路工程局常見問答集或高鐵票價調整案說明專區)
而台北到左營站的距離為 339.284 公里,所以 4.386 * 339.284 = 1488.099 元/人,四捨五入到十位,所以才變成了 1490 元。問題就出在四捨五入的部分,1488 若拆成兩段 744 的話,四捨五入都變成 740,總合就是 1480 省了 10 元。相反地,如果 534 拆成兩個 267 的話,四捨五入後就會多出 10 元。
拆票的時機
那到底要什麼時候要拆票,什麼時候不拆呢?這是個很麻煩的問題,只能夠用暴力法,把所有情況都試過,才會知道。這時手算實在太累,我們要藉助電腦的幫忙了。但「暴力法」只是個大方向,實際要如何使用「暴力」,巧妙各有不同。
此類的問題,我們通常會用「動態規劃」(Dynamic Programming),這是一種「用空間換取時間」的概念來寫程式讓電腦幫我們解決問題的方法。當然這細節並非一時一刻可以講的清楚的。不過,教電腦如何解決問題就是數學!若我們可以把生活上遇到的難題(尤其是需要重複操作的動作),跟所學結合,很多都能夠迎刃而解。
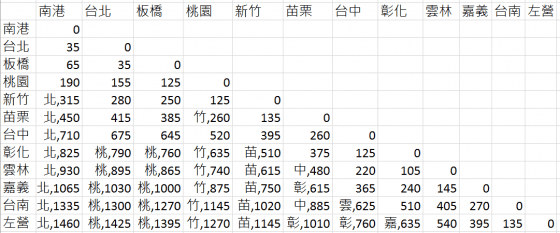
筆者利用最短路徑演算法中的「無圈戴克斯特拉演算法」(Acyclic Dijkstra’s Algorithm),經過一些改進,並利用電腦計算出所有最便宜的票要如何購買,結果如下表:
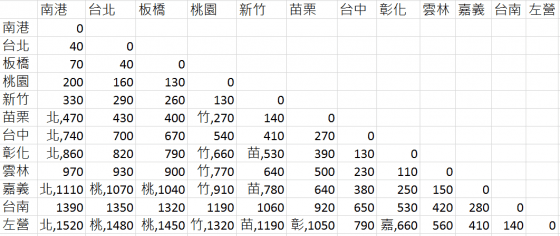
此表要怎麼查呢?是這樣的,不管南下或北上,都先視為南下,例如要買嘉義到新竹的票,先視為「新竹→嘉義」,查上表得「苗, 780」這串字,代表要先拆票買「新竹→苗栗」,剩下「苗栗→嘉義」這段,再查表,得「640」,沒有國字在數字前面,表示直接買是最便宜的。因此嘉義到新竹,就可以拆成「嘉義苗栗」與「苗栗新竹」兩張票買,只有 780 元,比原票價的 790 省了 10 元。
若是「台北→左營」的話,查上表可知,買「台北、桃園、新竹、苗栗、彰化、嘉義、左營」拆成六段票,會是 1480元,也是省 10 元。但這樣買的話,可能屁股還沒坐熱,就又要起來換位置了,還蠻麻煩的。
比較實用的是自由座。我們先來看一下現在高鐵自由座票價:
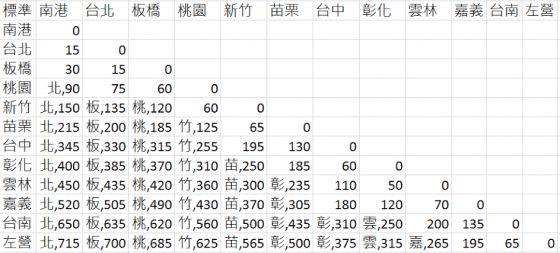
自由座全票價計算規則是把標準全票打 95 折後取比較靠近的 5 的倍數,也是類似四捨五入,其最佳的拆票表如下:
上表可以看出自由座長途車票拆票的話,最多可以省到 20 元。而且坐上車後,不用換位置,可以坐到底,非常方便。自由座優惠票(半票)最佳拆票表如下,最多可以省到 25 元:
至於商務艙屬於特殊服務,票價並不受交通部規範,所以它的計算方式並沒有用到「四捨五入」,而是每一段直接疊加的,所以怎麼拆票價錢都是一樣的。
至於團體票、早鳥票,實用性不高,這裡就不列出了。若讀者真的有需要,或是想檢驗自己跑出的結果,都歡迎來信跟我索取。
從上面的例子,有個很重要很重要的現象:「誤差是會疊加的!」標準全票因為用到四捨五入,所以會有誤差,最多差到 10 元,自由座把標準全票乘以 0.95 後再四捨五入,最多可以差到 20 元,自由座半票又再乘以 0.5 後再四捨五入,所以最多可以差到 25 元。若自由座半票,直接是把標準全票的原始票價乘以 0.95,再乘以 0.5,最後再做四捨五入的話,這樣誤差就小很多了。
事實上,筆者也把台鐵的票價表做了計算,下表是西部幹線山線的拆票表:
(台鐵各列車票價請參考:台鐵自強號票價查詢;台鐵票價計算方式請參考:台鐵票價試算。)
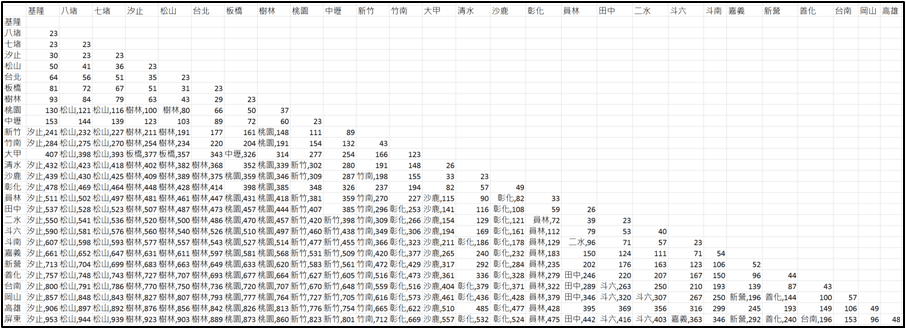
因為台鐵票價是四捨五入到個位數,所以即使基隆到屏東最長的路線拆成了 13 段票,也只省了 2 元。我想應該沒有人會為了省 2 元,自找麻煩吧。
考考讀者,若所有票價計算,皆改成無條件捨去的話,那會如何呢?改成無條件進入呢?
數學就在你身邊!
由以上幾個分享的例子(以及文末推薦的延伸閱讀),可以了解到數線、平面坐標、極坐標的制定概念,其實早就存在生活中,只是數學家將它更嚴謹地用數學語言描述出來。另外,同餘概念、最優化、微積分、演算法,這些求學過程各階段中學到的數學,也都可以運用到生活上。
大多的知識,其實都有其演進堆疊的過程,而且生活上的事物,常常也可以跟所學連結。因此,多學總是有益無害的,但通常我們的學習環境,都是只有學習,卻不常訓練學生如何去應用,「培養數感」其實就是「培養數學時常能跟生活結合的感覺」,有了「數感」就會有學習動機,有了學習動機,學生就會主動學習。
前陣子爆紅的手機遊戲 Pokémon Go,社群網站上,就可以看到各種神人分享所學與遊戲結合的結果:
- 演算法熟悉的人,就分享怎麼安排行走路線會最省時省力;
- 熟悉統計與最優化的人,就會分享如何撒花比較划算,提升抓到怪的機率;
- 學組合數學的人,可以計算所有怪獸搜集完全所需要時間的期望值、同樣的怪要轉換(transfer)誰、怪的體質與屬性的相剋分析、預估升級時間;
- 學電子的人會設計一個雷達裝置放在身上,路上遇到怪就會發出通知、利用無人裝置孵蛋;
- 駭客就會攔截遊戲訊號,取得怪的隱藏數值(IV)······等。
每個主題都不是一時一刻可以講的清楚,但看到不同背景的人,無不使用渾身解術,把所學運用到生活中,著實為我們帶來了不少正能量。
UniMath,You need Math,本期刊就是希望能培養大眾的數感而生,雖然每個人的學習背景不同,但只要能夠時時抱持著自己的知識都能用在生活上的信念,相信一定能蹦出不少的火花。
後記
編按:這篇文章近期在各大新聞也有許多相關的討論(例如:「數學老師幫你算好了 高鐵票分段買最便宜」 /以及後續的「高鐵票分段買最便宜?高鐵:恐造成行程延誤」),原作者郭君逸老師也在PTT上針對這個主題撰寫的初衷和一些網友的提問做了回答。而這些回應也讓文章的討論更臻完整,於是泛科學以後記的方式在此將原本的回文進行增補。
拆票有可能變便宜,我想很多人很早就知道了;如許多鄉民所講,只要利用加法還有比較大小,就可以知道了。其實會這樣想的話,表示已經可以把數學用到生活中了。
不過再更進一步去想你可能會想問:
- 有時拆票又會變貴,到底為什麼?是不是高鐵的Bug?
- 又怎麼拆會最便宜?
不管答不答的出來,會這樣想的人就是有著數學思維,Unimath的目的其實就達到了。而這篇文章的重點其實就是為了幫大家回答這兩個問題:
- 因為「誤差是會累加的」,高鐵票的計算方式是四捨五入到十元,有誤差,所以分越多段的誤差就會越大。
- 但怎麼拆才會「最佳」,這就要靠電腦的幫忙了。(演算法用在哪?後面會講)
而記者把重點放錯了,都著重在省20元,或是去售票機買不會影響別人之類的。 而且下的標題還很聳動!(這當然不能怪記者,因為不聳動的標題,沒人要點進去看!但至少重點要放對啊……)其實還蠻高興大家對這個主題有興趣的, 若有什麼好的科普主題或文章,歡迎投稿Unimath,跟大家一起分享。
下面是一些比較 boring 的部份,也順便回答一些鄉民的問題:
1. 演算法用在哪?不是只要加法就可以了嗎?
會這樣問的人,應該是沒有碰過程式。知道怎麼拆票的話,當然是直接把每一段票價加起來即可,所以只用到加法。但問題就是不知道怎麼拆,有時拆了還會變貴。
一個簡單的想法是:如果A到F中間有B,C,D,E站的話,每個站要分不分,總共2^4種切法都去試,這樣就是一種演算法。但這樣的爆力法,效率很差(指數時間),高鐵站可能還好,但如果像台鐵當中間的站點一多,連電腦也會算不完。
那要怎麼省時間呢?我觀察到了中間有很多重複計算的部份,例如: 計算A到F站的話,在試切C點時,也會把AC與CF的最佳解都算過了,後來就不用再重複算。 所以我就採取空間換取時間的方法(Dynamic Programming)把算過的存起來就不用再重算, 這樣的演算法就會快很多,即時算台鐵的所有站的分票,也是按個Enter馬上就算完了。
整個演算法雖然是我自己想的,後來還是查了一下書, 發現在演算法書中,最短路徑一章就有很多類似的東西,然後我的演算法跟Dijkstra無迴圈的版本很像。 (其實還是有點不同只是原理相同, 有興趣的同學可以自己寫程式列出所有站點之間的分票方式,比較能體會其奧妙,程式其實很短。)
2. 誤差疊加很重要,求學時老師每次講,台下的我聽了都沒感覺。
明明多項式計算就代進去就好,為什麼還要改成巢狀計算; 矩陣就直接乘就好,為什麼還要對角化、Jordan Form……然後就會在台下說,學這個到底要幹嘛、多此一舉, 後來等到自己遇到麻煩了,才知道自己當時的無知。
3. 時間成本很重要,誰會省這20元。
這當然是這樣,現在比較忙時間都不夠用,我自己每次坐高鐵都坐直達的,誰想每站在那裡換位置!省錢只是文章的手段,讓讀者願意點進來看,但重點不在此,不要再被記者拉著走了。
4. 數學教授整天算一些沒用的東西。
其實有沒有用每個人都不同, 否則籃球員為什麼要一直把球丟到籃框裡? 畫家為何要畫畫?攝影不就照起來,再用一些濾鏡就好了? 這都是他們的工作、成果、興趣。 自然會有欣賞的人,自然也都有它的價值在。
5. 只要會加減乘除就可以活的好好的,為什麼要學這麼多?
這老生常談了。這就讓大家幫忙回答吧! 連加減都不會,也是可以活的好好的。
- [數學妙用]不會測速的測速相機,郭君逸,UniMath。
- 生活中的數學:交通篇(上),郭君逸,UniMath。
- Pokémon Go 指南:如何用數學幫助你 Catch ’em all,賴以威、陳宏賓,UniMath。
本文轉載自 UniMath,《高鐵票分段買比較便宜?》
作者簡介:郭君逸 - 國立台灣師範大學數學系助理教授、魔術方塊收藏家。
主要研究興趣為組合、圖論、演算法。近年來致力於科普的推廣,喜愛玩各種數學遊戲、益智玩具以及各類型魔術方塊。目前為世界魔方聯盟(WCA)台灣地區認證員。曾開設整個學期的魔術方塊通識課程,跑遍全台進行魔術方塊系列演講。
關於 UniMath:UniMath (You Need Math)是一個 Online 數學媒體,