上回介紹了我運用數字感把風靡世界數千年的古印度數學──吠陀方形(Vedic square)加了一個維度以後定義與發明了吠陀立方(Vedic cube)[1]。
吠陀方形就是將大家熟悉的九九乘法表中每一個數字進行位數根(digital root)運算,例如說 5 乘上 5 會得到 25,把 2 加上 5 得到 7,這個 7 就是 25 的位數根也是吠陀方形裡座標點(5, 5)的數值。吠陀方形在西元 770 年被穆斯林納入伊斯蘭的數學知識體系之中 [2]。
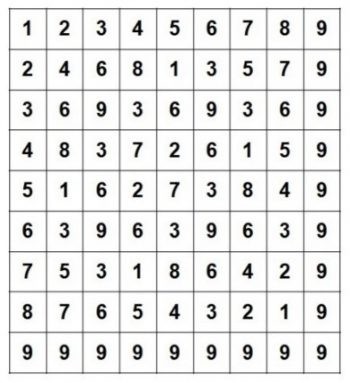
其中位數根所在的位置互相連結後組成的胚騰(pattern)構成了特定的幾何圖案如下圖,晚一點還會繼續用到:

吠陀立方則是將吠陀方形從平面延伸成立體,也就是三個數字相乘的三維乘法表(9 × 9 × 9),是整個立方體中各個座標點的數字進行位數根運算後的結果,可以用函數 D(X, Y, Z)代表吠陀立方中座標(X, Y, Z)該數字的位數根,實際運算時的數學式為 D(X × Y × Z)。例如座標點(2, 3, 5)在吠陀立方中的數值即為 D(2 × 3 × 5)= D(30)= D(3)= 3。
然而,上回提到以軟體繪出吠陀立方中的位數根胚騰散布情況相當複雜(可見上一篇),難以看出這些座標點在空間中構成的意義,因此需要以其他方法解析。結束有點長的前情提要以後,這一回我要以樓層法(Floor method)深入解析吠陀立方,帶大家往更高的樓層邁進,發現數學蘊含的規律。
既然無法一眼就看出三維空間的位數根胚騰散布情況與這些座標點在空間中構成的意義,那何不把吠陀立方視為有 9 層樓高如同建築物的立方體,這方法我稱它為樓層法。下圖是吠陀立方 1 樓至 9 樓的所有數值,樓層區分的原則是 Z 軸的高度。

基本圖樣與行列的代碼定義
把 1 樓至 9 樓的所有數值都列出來以後,就可以來進一步觀察位數根在不同樓層之間構成的圖樣,這些圖樣其實是幾種基本圖樣(basic pattern)的變換或是變形,這些基本圖樣是吠陀方形中出現的幾何圖樣。
為了方便稱呼與後續討論,必須先定義這些基本圖樣的名稱。像是數字 1 在吠陀方形中所組成的圖樣,就稱為 D1F1,因為是基本圖樣所以可以將 F1 省略,簡稱 D1;而數字 8 構成的圖樣 D8F1 為數字 1 對鉛直線的鏡射或說旋轉 90 度後的結果,簡稱 D8,其他數字構成的圖樣名稱以此類推。

2 樓以上樓層代碼中的 F 則不可省略,例如位數根 1 於 2 樓的圖樣稱為 D1F2,位數根 4 於 7 樓的圖樣稱為 D4F7,其他位數根於其他特定樓層的圖樣代碼也依照此原則表示。至於行列代碼的定義如下,以 C2F1 表示吠陀立方中 1 樓的第 2 行,即 246813579,其他樓層的行列以此類推,實際上行與列的組成數字相同,在此以行(column)代表行與列。
動手發現數學胚騰
介紹完代碼以後,建議大家實際拿出筆來試著自行發現數學胚騰。初階的玩法是選定一個數字,例如自己生日的位數根,也就是俗稱的生命靈數。例如泛科學的生日是 2011 年 11 月 4 日,生日位數根是 1,就把 1 到 9 樓的數字 1 都塗上顏色或是圈起來做標記,再對照前面提到的基本圖樣 D1 至 D9 看看兩者對應的關係。
如果還意猶未盡的話進階玩法是下載吠陀立方每一層樓的 pdf 檔案,觀察其他 8 個數字在每個樓層的數學胚騰與其變換的規律與規則,檔案中同一層樓印 9 個為了方便大家觀察完自己選定的數字以後,還可以觀察其他 8 個數字在同一樓層的數學胚騰,畫記數字時才不會把圖樣混在一起。
不同樓層的位數根圖樣變換
經過這些觀察以後,我發現同個位數根構成的圖樣在不同樓層之間也具有對稱、鏡射的性質,像是位數根 1 在 2 樓(D1F2)與 7 樓(D1F7)的圖樣其實為 D5 與 D4,兩個圖樣在 X-Y 平面的投影為相互對鉛直線鏡射,此外 1 樓與 8 樓、3 樓與 6 樓、4 樓與 5 樓也都具有這樣的性質。也就是說 5 樓至 8 樓的位數根圖樣可分別由 4 樓至 1 樓鏡射得到,位數根 1 在各個樓層構成的圖樣如下圖:
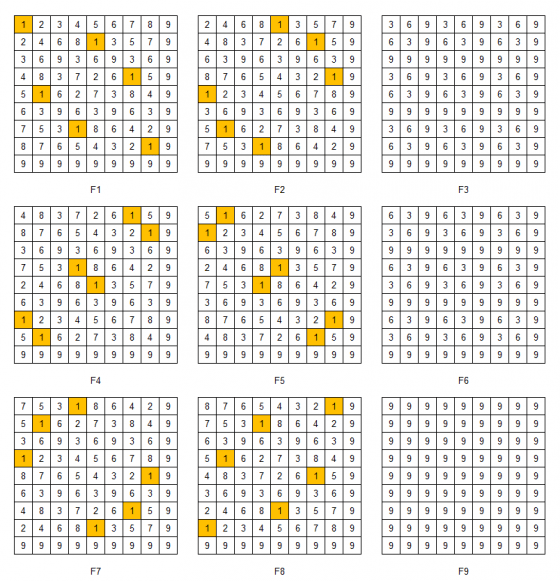
有趣的是,這些位數根胚騰在不同樓層之間變換的規則,可由吠陀方形(1 樓的 X-Y 平面)清楚看見。下圖同樣先以位數根 1 為例解釋。我把位數根 1 在不同樓層之間的圖樣變換紀錄在下圖(a)表格中的圖樣欄位,該欄位代表在 X 樓時,位數根 1 構成的圖樣是對應吠陀方形中哪一種基本圖樣。
我在研究時發現,位數根 1 在吠陀方形中 X 位置出現時對應的 Y 值,就是基本圖樣出現的順序!例如說下圖(b)當 X 為 2 時對應的 Y 值為 5,D1F2 對應的即是 D5 圖樣,其他樓層 X 的圖樣變換可由箭頭指向的 Y 值辨認之,像是可以看到由 X 樓對應的 Y 值與箭頭辨別出在 4、5、7、8 樓對應的圖樣各為 D7、 D2、 D4、 D8。

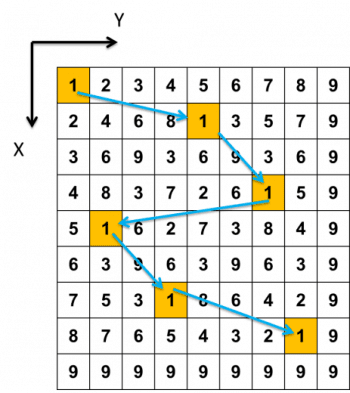
圖樣變換解釋
由吠陀方形指認吠陀立方位數根胚騰的變換順序是巧合還是有根據呢?由上面我們知道 D1F2 會等同 D5 圖樣,D5 圖樣對應的是吠陀方形中位數根 5 的圖樣。由定義我們知道 2 樓的組成數字是 1 樓的所有數字都乘上 2,那什麼數字乘上 2 之後的位數根會等於 1 呢?從乘法表中於 X = 2 的地方,只有 Y = 5 此相對應的位置,才會得到位數根為 1,因此 D1F2 = D5。
在 4 樓我們發現 D1F4 = D7,也可以想成是原本在 1 樓的 D7 圖案,到了四樓以後乘上 4 之後的位數根自然而然就變成了 1。如此一來便能解答為什麼 3 樓、6 樓、9 樓都沒有1(以及 2、4、5、7、8)呢,因為沒有任何數字乘上 3、6、9 之後的位數根會是 1 啊!除了位數根 1 之外,其他的位數根都遵循上述的原理,讀者可由前面提供的檔案自行對照。
只要圖解吠陀方形,就可以知道其他位數根於特定樓層中會是哪一種圖樣。也就是我們可經由二維平面的吠陀方形進一步了解三維空間的吠陀立方。吠陀方形這個二維平面不只為三維空間的一個剖面或是一樓而已,更是了解三維空間位數根胚騰非常重要的基礎。
若是想用方程式求得位數根 p 在 q 樓的圖樣會與哪一個位數根 r 在 s 樓的圖樣相同,可利用此式判別與求解未知數 D(p × s)= D(q × r),若等式兩邊相等則 DpFq = DrFs 成立。s = 1 時求得的 Dr 即為對應的基本圖樣,表示 Dr 位置的位數根在 q 樓層會是 p 位數根。例如說想要知道位數根 7 在 8 樓的圖樣會對應哪一個基本圖樣 Dr,可以用D(7) = D(8 × r)得出 r 為 2,D7F8 = D2 與直接觀察的結果相同。
圖樣可以多重組合
有的時候特定數字於特定樓層構成的圖樣將會不只涵蓋一個基本圖樣,而是多個基本圖樣組合而成。舉 D3F3 的圖樣組合當做例子,下圖左方在吠陀方形可以看到 X = 3 時,對應的 Y 值有 3 個,分別是 Y = 1、4、7,對應的基本圖樣為 D1、D4、D7。下圖右方顯示了 D3F3 的圖樣,是由 D1(黃)、D4(綠)、D7(藍)這三種圖樣組合而成的,以數學式表示則為 D3F3 = D1 + D4 + D7。
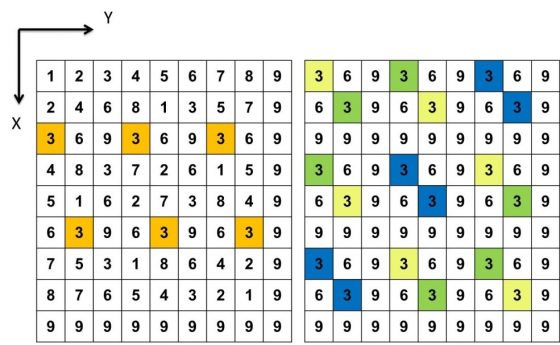
從上圖可以發現 X = 6 時對應的數值為 3 也有 3 個,分別是 Y = 2、5、8,也可寫成 D3F6 = D2 + D5 + D8,表示位數根 3 在 6 樓是由 D2、D5、D8 圖樣組合而成。類似的多重圖樣組合尚有 D3F6、D6F3、D6F6、D9F3、D9F6、D9F9。
圖樣多重組合的原理可以解答為何 9 樓每一個位數根皆為 9,因為不管 1 到 9 是哪一個數字,乘上 9 之後都會是 9 的倍數,位數根也會是 9,所以在 9 樓每一個位數根皆為 9,也表示了 D9F9 為所有的基本圖樣組合而成。以數學式表達可以寫成 D9F9 = D1 + D2 + D3 + D4 + D5 + D6 + D7 + D8 + D9。
吠陀方形除了隱含三維空間位數根圖樣變換的根據之外,還蘊藏了不同樓層之間行列變換的規則,例如吠陀立方 2 樓的行順序事實上為 1 樓的行順序乘上 2,也是 1 樓第 2 行對應的數字。2 樓的 1 至 9 行的組成順序為 1 樓的第 2、4、6、8、1、3、5、7、9 行。2 樓的第 1 行等同 1 樓的第 2 行,以代碼表示則為 C1F2 = C2F1,其他樓層以此類推。
若是想知道 i 樓的第 h 行列會與 k 樓的第 j 行相同,可利用此式判別與求解未知數D(h * i)= D(j * k),若等號兩邊相等則 ChFi = CjFk,k = 1 求得的 Cj 即為對應的基本行,表示 Cj 在 i 樓層會出現於第 h 行。這個公式和前面的是不一樣的。
次回預告
樓層法專注在解析吠陀立方各層本身的性質以及與吠陀方形的關係,較難探討位數根胚騰在三維空間中彼此的相關性,所以下回將會帶大家以第二種方法──對稱面法切入吠陀立方的中心一探究竟。
參考資料
- Lin, C. Y. Digital Root Patterns of Three-Dimensional Space. Recreational Mathematics Magazine, 3(5), 9–31, 2016.
- Jones, L. “Mathematics and Islamic art”, Mathematics in School, 18(4), 32–35, 1989.