文/黃誠熙(Sky Huang),目前為UCLA材料系博士候選人
我們都有這樣的經驗,在工作、學習的時候會一邊想著玩樂的事情;雖然身體還坐在桌前,心已經飛到窗外遊玩去了,非常沒有工作效率。又或者,有時受不了誘惑,跑出去玩樂了半天,一回到書桌前,內心感到無比內疚,反而激發起破表的效率,快速完成工作。

這是相當普遍的現象,有死線(deadlines)當前時會更為明顯,效率值無限上升。在心理學上也有相當多的研究,尤其在死線前的效率提升方面。例如說,有時候人們在面對deadline的時候,會為自己設置另一個「自己的死線」(self-imposed deadlines),以防止自己拖延而超過實際上的死線。心理學家發現,雖然這樣有助於提升在死線前的工作成效,但是增進效率的效果並沒有外部死線來得強烈(很可以理解,錯過外部的deadlines就要被炒魷魚拉,錯過自己設定的deadline只是有點沮喪而已)[1]。
然而,這邊想跟大家討論的不是心理學的部分,而是如何使用數學來增進工作效率!更精確地說,如何使用「內疚學習法」來增進工作效率。
內疚學習法顧名思義表示當你學習的時候,是處在內疚的狀態,也就是說,為了增進學習效益,在學習之前先花一段時間玩樂,玩樂結束後會覺得很內疚,因此學習效果大增,比一邊念書一邊想著玩樂效果還要好。筆者自己本身在考升大學考試時發現了這個現象,但同時也發現,要是花太多時間玩樂,雖然內疚值會累積很高,效率非常好,但是因為玩樂佔去的時間太多,剩餘時間太少,無法將效率轉成實際效果。因此,內疚值累積和學習時間必須要取得良好的平衡,才能發揮內疚學習法的最大效益。
下面我們用數學來推論內疚學習的最佳解。首先,我們知道唸書的時間是隨著玩樂的時間線性的遞減,譬如說,假如我們總共可以唸書的時間是8小時,花了3小時玩樂,那就剩下5小時可以唸書。如果我們把總共唸書的時間等比縮放(rescale)變成1,而玩樂時間是t,則剩下可以唸書的時間就是(1-t)。
(編按:注意喔!以下是數學的推論,並非心理學研究)
接下來要知道的就是:讀書效率如何因玩樂時間的增加,內疚值的累積而增加。當我們知道效率隨玩樂時間的變化eff(t)之後,即可計算總學習成效,也就是f(t) * (1-t),事實上效率函數應該是兩個時間的函數,一個是玩樂花費的時間t,一個是當開始唸書之後效率隨時間T的變化,因此為f(t, T),而真正的讀書效率為積分。這邊假設開始唸書之後的效率為一定值,因此積分可以簡化為f(t) * (1-t)。
效率成長的變化曲線沒有一定的樣子,因此必須使用假設的模型。下面使用兩個假設來計算最佳的玩樂時間。
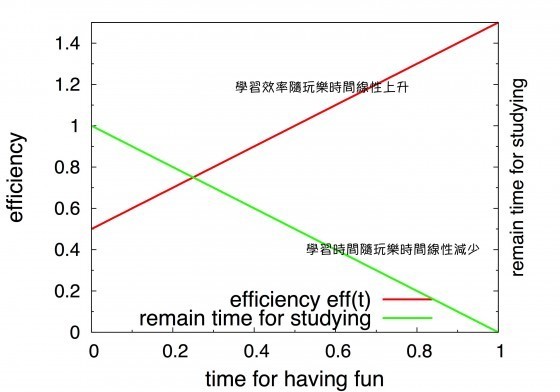
讀書效率正比於玩樂時間(反比於剩餘讀書時間)
假設讀書效率 eff(t)= a + bt
(如下圖,綠線為剩餘學習時間,紅線為效率變化)
- t為玩樂時間
- a是基本的讀書效率(沒有使用內疚學習法)
- b則是效率隨玩樂時間增加的斜率
由於(1-t) 為剩餘可以用來學習的時間,最後學習成效是時間 * 效率,即表示:
學習成效f(t) = eff(t) * (1-t) = (a + bt) * (1-t)
在得到學習效率函數之後,我們只要求得f(t)的最大值,就可以知道最佳玩樂時間,可以得到最好的讀書成果。求最大值的方法之一為將f(t)對時間微分=0,即為:d f(t)/ dt =0
可以求得必須花多少時間玩樂學習效益才會最大化。這個方程式的解為:
t = 0.5 – a/2b
a和b都必須是正數(a為沒有使用內疚學習法的學習效率,為正;b為使用內疚學習法時效率隨玩樂時間的上升斜率,為正。)
檢視這個式子,我們可以知道因為時間永遠為正數,若是t<0,表示內疚學習法為沒有效率的學習方式,因此只有當0.5 – a/2b大於零時,才可以使用內疚學習法,最終我們可以得到 b > a(小提醒:a為基本學習效率,表示沒有使用內疚學習法的學習效率;b為效率隨玩樂時間上升的斜率)。這表示如果花費所有唸書時間來玩樂時,在最後一瞬間準備要唸書時,念書效率可以提升為基本學習效率的兩倍時,則內疚學習法是有效的。
結論:先做一個實驗,假設你把所有時間拿來玩樂,你必須要保證在花掉幾乎所有時間玩樂之後,你的內疚值累積足夠讓讀書效率提升到原本的2倍,你才可以考慮使用內疚學習法。而內疚學習法的最佳化效率為:把0.5-a/2b的時間拿來玩樂,剩下的時間唸書,也因此若是玩樂的時間超過所有時間的一半,那一定不是有效率的內疚學習法。
當讀書效率的增加有極限值
在實際狀況下,效率是會受限於學習的人的學習能力、科目的難度…等等,因此,隨著玩樂時間上升,效率值的提升不會一直線性上升,而是有一個極限值,效率的增加就會慢慢趨於緩和並逼近最大效率值。下圖為在此假設下念書效率隨玩樂時間t的變化:
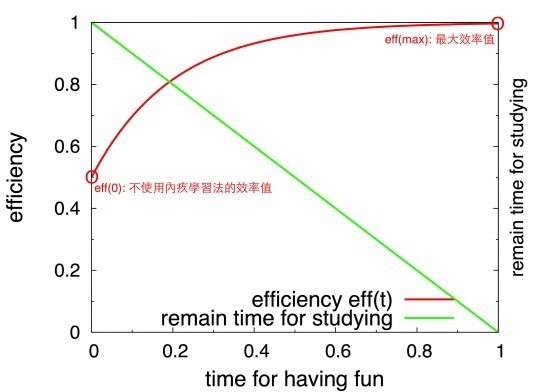
我們可以用一樣的方法最大化eff(t) * (1-t)來求得最佳玩樂時間(可以使用exp函數來描述,eff(t)= A – a*exp(-bt),然後再次使用df(t)/dt=0 求解最佳玩樂時間。但是此數學處理有點複雜,有興趣的讀者可以自行研究。)。
結論:當有一效率最大值時,整體最佳玩樂時間會比上述第一種模型來得少(從圖形中觀察可得知)。而可實行內疚學習法的狀況會越來越嚴苛。最佳的玩樂時間長度將會大幅遠離整體時間一半的附近,而趨向更小的值(1/4或是更小)。
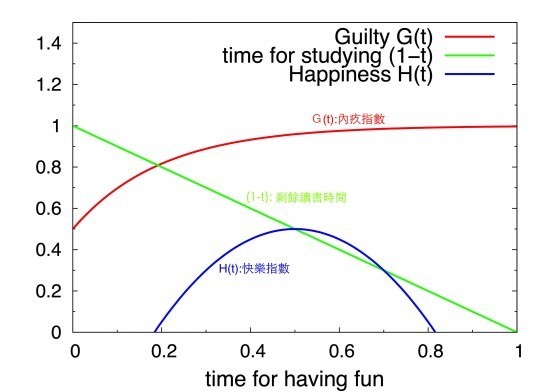
另外一個要考慮的因素是快樂指數。我們會發現,若是太過內疚,譬如說太接近deadline還沒有把作業做出來,會產生焦慮的心情,進而影響工作效率,並減低內疚學習法的效果;但是另一方面來說,玩樂也會帶來快樂,進而提升工作效率。在考慮快樂指數後,最佳化變得更加困難。唸書成效函數可以寫成:
f(t)= H(t) * G(t) * (1-t)
- H(t):快樂指數
- G(t):內疚指數
- (1-t):玩樂之後剩餘的唸書時間
三個函數分別作圖如下:
最終結論:
適當的玩樂對於學習成效是有好的幫助的;然而,過量的玩樂將導致學習成效低落(恩,或許大家早就知道了) 。而最佳的玩樂時間必須遠小於整體時間的一半,至於實際的最佳玩樂時間長度則決定於個體產生內疚的程度以及內疚心理造成效率提升的程度。
在心理學上,大致上還是視「拖延」為不好的行為,在此前提下研究人類為什麼會拖延,以及如何可以避免拖延行為發生。這邊筆者則是從數學模型提供另一個角度,讓大家思考拖延、玩樂行為對於整體成效的提升/降低,以及玩樂/學習的比例分配。
參考資料: