作者:Shane L. Larson
譯者:王人德(Ray)
我為什麼喜歡網路上的流言呢?因為它們的的確確代表著現代生活中極為荒誕的事物,說起來也不特別啦,但顯然我算是處在一群科學家中的少數族群。我可以理解那些對於時事的評論(或是網路流言),或者願意去看一部好萊塢的鉅作(像是《世界末日》),這些事物跟我腦中處理科學的機制完全搭不上邊,但它們卻和我平常所思考的事物產生衝突,我的腦因而產生化學反應,這些衝突感也為我帶來充實以及愉悅。這種「實事不求是」的精神其實對科學家們來說是非常痛苦的。
為什麼呢?科學家們已經被訓練成為一個不帶任何感情的個體,一切都只為了能夠更公正地觀察著這世間萬物。也就是說,他們已經完全和自然背道而馳,也總是將我們個人的想法像是放在一張桌子上一般,透過放大鏡來檢視。不過,我們終究是人類。但科學這項機制就是設計來保護我們的,不是嗎?我們想要並且需要一直重複做著實驗,而所得到的結果也需要被大家檢視以及懷疑,就為了找出是否哪個小細節有所矛盾。當我們發現了有矛盾的地方,而後新的實驗以及新的想法又出現了。這整個過程一直不斷地、不斷地重複著,永遠都不會停止。縱使實驗後所得到的新數據和想法被大家所肯定了,也只是被大眾認定為這是最好的「實驗示範」,快點改觀吧!若你不在科學這門學問中懂得變通,那你就錯了。若你一直墨守成規,就算你得到令人讚嘆、完美的數據,那麼你也錯了。科學這門學問會自行修正錯誤的數據,所以呢,我們做越多的實驗,我們會越來越了解大自然,對於那些自然界中的迷思也會越來越少,從小學的那些錯誤資訊也會日趨減少。
為何會日趨減少呢?而「高可能性」和「低可能性」又是甚麼意思呢?我們又該如何去理解呢?再一次地,為了理解這一切,我們又要回到先前所提到的「網路流言」了。曾經這麼流傳著:當有一百萬隻猴子站在一百萬台打字機前開始打字,最後一定會完成整部莎士比亞所寫的「仲夏夜之夢」。
科學的美在於它的接觸範圍非常的廣,而且早已有著合適的方法去套用在你所感興趣的課題上,例如我們先前提到的想法「猴子竟然能夠完成一部莎士比亞的作品?」(這是一個很有趣的智力測驗,雖然也有人認為這樣的事情就像電影「決戰猩球」一樣令人害怕。 )
我們來討論一下「可能性」吧!這是一個被人們濫用的概念,而且常常被用在稀奇古怪的地方,但我們可以從這些基礎的假設當中來思考那些網路迷因(meme)。這裡是一個簡單的範例 : 擲銅板。(但我們這次要擲的是Oreo餅乾,正反兩面各是巧克力以及原味。) 遊戲規則如下 : 若結果是原味,你就可以得到那片餅乾;反之,若是巧克力,餅乾就屬於我。對於實驗結果,我們兩個人有著同樣的利害關係。現在假設我們兩人是公平的,沒有任何方法能夠控制其變因,就暫且稱它「公平的Oreo餅乾」吧!(其實就跟硬幣和骰子是同樣道理)
所以當我擲一枚餅乾,你有一半的機率可以得到它。這是甚麼意思呢? 也就是說你擲到原味的結果是兩種結果中的其中一種。
你想要的結果/有可能的結果 = 1/2 = 0.5 → 50%
一個對數學有著狂熱的人可能會向我們解釋 : 當我們拿著每袋各裝有100個餅乾的袋子,總計有10袋,而後將每一片像餅乾擲硬幣一樣,那麼平均來說,每一袋裡面都會有50片是我們想要的結果。「平均來說」是一個很重要的敘述─對於數學的困惑、爭議、發現以及理解,都隱含在這個敘述當中。統計並非一直都正確,稀奇古怪的事確實會發生機率遭到推翻的情況,所以他們才會被稱為「事變」!
那麼我們來點更複雜的問題吧!假設現在我們兩個人想要一次擁有兩塊餅乾,那麼機率又會是如何呢? 我將這個想法製作成下列的表格。有幾種方法可以得到原味Oreo餅乾呢? 兩種:在第一輪或者是第二輪拿到;同樣地也有兩種方法可以得到巧克力口味:在第一輪或者是第二輪擲到。
以上就是我們在這場良性競爭下所得到的結果。依序是:你得到所有的餅乾(G1-G2)、我得到所有的餅乾(C1-C2)、以及各自分攤自己的餅乾(C1-G2和G1-C2),我想應該不會影響到我們兩個人的友情吧?
看看這表格,你有四分之一的機率(1/4 = 0.25 = 25%)成為「Cookie Monster」拿走兩種餅乾。那麼我能夠不做表格就知道這結果嗎?當然!只要將每件事情發生的機率相乘就能夠得到你想求的獨立事件之機率。我們先前說過在正常情況下想得到原味餅乾的機率為50% (1/2 = 0.5 =50%),那麼如果我擲了兩次,就會得到 :
天啊!但老實講:就算我贏得了兩塊餅乾,到最後我還是會分你一塊的啊 😛
現在,我們言歸正傳吧。關於猴子和莎士比亞。經過了一番搜尋之後,我還是找不到有哪個人會知道仲夏夜之夢裡頭到底有幾個字!其實我大可寫出一個程式來計算裡頭的文字量,但我還有名聲要顧啊!怎麼可能讓這種怪事讓大眾知道呢!我們還是想點簡單一點的方法吧。
試問:猴子隨機在鍵盤上打出一個英文單字的機率是多少?就拿「cookie」這個字來當範例吧。我們假設鍵盤上有27個鍵─26個英文字母以及空白鍵。猴子打出任何一個字的機率為27分之1(1/27 = 0.037 = 3.7%) 。而先打出「c」再打出「o」的機率如下:
這並不是個大數字吧? 那麼打出完整的單字「cookie」呢?
我們可以發現,猴子想要隨機打出「cookie」這個字的機率就高達40億分之1!那麼一部莎士比亞的劇作難度就更高了。裡頭有更多的字需要訂正呢!
但是呢,「猴子」們在網路上更加活躍(當你看過網路上的評論或者是部落格就能夠理解)。當有一大群猴子開始打字,理所當然地一定會有一隻能夠完成這項壯舉,就讓我們來看一下這個有趣的想法吧:仲夏夜之夢一共有2165行,而每一行大致上有45個字,因此:2165(行)X 45(字) = 97425(字),猴子們有97425個字需要去完成。
一隻猴子完成這件事的機率會是多少呢? 以「cookie」這個實驗當作範例,1/27一共要相乘97425次,就成了97425分之一了(以數學符號來表示就是1/2797425)。如果你將27相乘97425次,那數字不只是大,更是令人嘆為觀止!因此1/2797425理所當然是個超級小的數字了。在科學中,我們學到了如何簡潔有力寫出極大和極小的數字,也就是科學記號,方法其實很簡單,只要將在一個數字後面乘上10的次方就行了。
舉例來說吧,1×103的意思就是將10連乘3次後再乘1(也有此一說:每當要乘以10時,就在數字後加個0),因此,1×103 = 1000,理所當然地,7×104 就是7x10x10x10x10 = 70000。
將這個想法套用在猴子實驗身上之後,我們該怎麼表達2797425呢? 科學記號中,這也可以轉換成1×10139,450(1後面有139,450個0)。所以一隻猴子想要完成一部仲夏夜之夢的機率將會是1/10139,450。換句話說,在我們開始實驗之前,我們需要先收集到10139,450隻猴子。
這是個令人瞠目結舌的數字啊!這麼龐大的數字根本不存在我們所認知的宇宙當中。例如:一個Oreo餅乾大約等於7×1023個原子;相較之下,太陽大約等於1×1057個原子;而整個銀河系大約等於1×1069原子;而在我們可見的宇宙中大約包含1×1080個原子。所以倘若你想要讓一隻猴子意外地打出一部莎士比亞的劇作,你會需要比整個宇宙的原子數量還要多的猴子,似乎是不可能的呢。
其實做這些實驗只是有趣的消遣娛樂而已,但他們真的跟現實世界有所關聯嗎?當然,統計一直與我們的生活息息相關。其實呢,Oreo實驗所使用的計算方式也能套用在其他事情上;得了癌症之後的存活率、無線網路一次可以支援幾支手機、以及計算我們未來登上那未知的星球─火星的成功率。(http://mars.jpl.nasa.gov/)
猴子實驗只是一個對現代文化的反思,也從來沒有想要去挑戰科學,但它卻真實反映了非常人性化的一面─也就是根深蒂固在我們心中的,那種人類無法掌控整個宇宙的無力感。但不可否認的─藝術和科學是我們唯一可以抒發無力感的管道。天才莎士比亞因為沒有同儕之間的影響,所以他能夠以純人類的角度來思考並且創作故事,不只啟發了我們,也深深影響著後代。同樣地,科學也是那些因為那些天才們努力不懈地發掘才有今日的成果。我們能夠發現新事物,並且藉由所學的知識來改善生活品質。我們能夠將所發現的事情記錄下來,而後啟發我們的子孫們,使他們更加了解自己所生活的世界中的點點滴滴。
對於透過科學來了解事物這件事,我深信不疑,甚至是相當有自信。我很欣慰並且敬畏我擁有「發現」的能力。但這並不代表每個問題都能夠容易解決。發展出能夠穿梭於星球間的科技依舊困難;完全了解動物(或植物)的演化依舊困難;了解癌症的本質也依舊困難。但我還是有信心,只要給我足夠的時間、足夠的資源、以及充足的腦力,任何問題都可以得到一個答案,而你們也應該這麼想。「盡信書,不如無書」,再看一次電影「世界末日」吧,雖然是個逃避現實的科幻故事,但卻也同時表達了一件事:科學永遠在你身邊。
原文:The Commonality of Armageddon, Oreos, & Shakespeare’s “A Midsummer Night’s Dream”



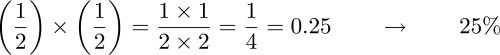
































-200x200.jpg)







