
猴子問題成為機率論裡統計機制的題目,最早是出現在法國數學家埃米爾.博雷爾(Émile Borel)於一九一三年所寫的文章中,題為〈統計機制與不可逆性〉(Mècanique Statistique et Irrèversibilitè)。文中說,如果給定足夠的時間,一隻猴子可以在鍵盤上隨機敲出莎士比亞全集。當然,「足夠的時間」指的可能是無限長。
英國物理學家亞瑟.艾丁頓公爵(Sir Arthur Eddington)對於隨機性的態度則更為開放,他在一九二七年受邀到愛丁堡大學的紀福講座(Gifford Lecture)演講時說:
「如果我把手指放在打字機的按鍵上隨意亂敲,這個行為『可能可以』造出詞意通順的句子。如果一批猴子大軍亂敲著打字機,牠們可能可以寫完大英博物館中所有的藏書。」
讓猴子敲出指定字句的機率有多高?
現在,讓我們把目標簡化一下。先別指望到大英博物館,也不要談論莎士比亞全集,連十四行詩都先擱在一邊,只討論這一句:
Shall I compare thee to a summer’s day?(我怎能將夏日與你比擬)
如果一隻猴子要能依照這樣的字母順序敲出來,我們肯定會認為這是極罕見的巧合。這可能性有多大呢?絕對非常微小!

假設鍵盤上只有二十六個鍵,只能敲出小寫的字母,那麼猴子要敲對「shall」第一個字母的勝率為 25 比 1。而每一次的敲擊與任何一次的敲擊之間都互為獨立,因此,正確打出頭五個字母的機率,只有26×26×26×26×26=11,881,376 分之一,勝率為 11,881,375 比 1。不過這只是第一次打字就成功的機率,麻煩在於應該不只有一次機會,而有很多很多次。
讓我們算一下第一次嘗試時無法成功打出單字的機率,即是 1–(1 ⁄ 26)5,大約為 0.99999991583,幾近必然會發生。試驗 N 次之後,猴子沒敲對的機率為 (1–(1 ⁄ 26)5)N。
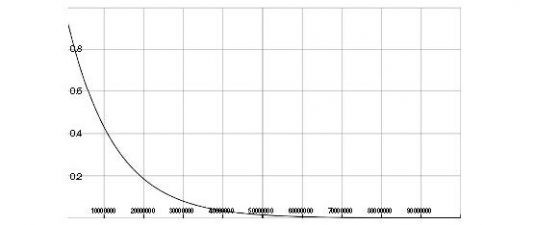
N=8235542 時,牠會有超過一半的機率打對莎士比亞著名的十四行詩的第一個單字。上圖可以說明,在經過約莫五千萬次試驗之後,沒有打出「shall」的機率趨近於零 。[10]
內容越複雜,打對的機率越低
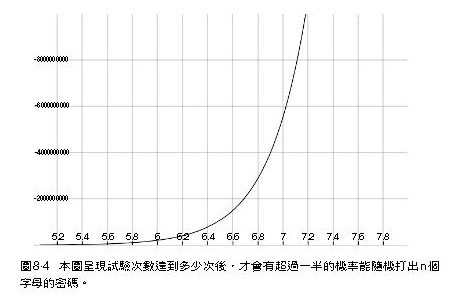
把這方法應用到密碼保護裝置上,可以得知,藉由隨機敲打字母,電腦程式就能夠輕易地破解由五個字母組成單字的密碼。如今,就連相對慢的電腦,中央處理器(CPU)都可以在少於十秒的時間內試驗五千萬次。但如果你把密碼多加上一個字母,試 214124096 次之後,才會有一半的機率能破解密碼。困難度會隨著字母(包括混合使用字母、數字及符號或大小寫)的增加而呈指數增加。請見下圖。
隨機在鍵盤上亂打,敲對 π 前六個位數的機率為 0.000001,也就是百萬分之一的機率。如果一千隻猴子中,每一隻猴子都敲鍵盤一千次,出現敲對 π 的前六個位數的機會便會超過一半。或許,這會使你覺得 π 畢竟不是那麼特殊的數,不過,這當然是因為我們只取前六個位數而已。接著,取 π 的前一百個位數。就算隨機挑選宇宙間每一顆沙粒與星辰直到時間的盡頭,寫出 π 的前一百個位數的機率還是幾近零,難以動搖。
一九一三年,埃米爾.博雷爾要我們想像一百萬隻猴子,每天花十小時隨機敲擊打字機:
Les contremaîtres illettrés rassembleraient les feuilles noircies et les relieraient en volumes. Et au bout d’un an, ces volumes se trouveraient renfermer la copie exacte des livres de toute nature et de toutes langues conservés dans les plus riches bibliothèques du monde.
(不識字的領班會把髒掉的紙收集起來疊成冊。某一個歲末之際,這些書冊會恰好與世界上藏書最豐富的圖書館中,所有語言與種類書籍的冊數相同。)

而英國物理學家及數學家詹姆士.金斯爵士(Sir James Jeans)則在其著作《神祕的宇宙》(The Mysterious Universe)中這麼寫:
有人說,我想是赫胥黎吧,把六隻猴子放在打字機前胡亂敲打,數十兆年後的某個時點,會恰好打出所有大英博物館中的藏書。
如果我們檢查某隻特定猴子所打的最後一頁內容,發現在亂打的情況下剛好打出莎士比亞的十四行詩,我們想必馬上就會認定這是一起驚人的意外事件,但如果我們看遍了數百萬頁猴子在難以計量的時間內所打的內容,我們滿篤定會從中找到胡亂敲打的產物──莎士比亞的十四行詩。
同樣地,數十兆顆恆星在太空中隨意地遊蕩數十兆年,必將碰上各種意外,也必將在一定時間內製造出有限數量的行星系統。然而,若與天空中的星星數相比,行星系統的數目肯定非常小。
用電腦模擬的猴子,打出了前十九個字母
用電腦虛擬的猴子來模擬執行猴子問題。二○○四年八月四日,電腦虛擬的猴子在經過 42162500000 乘以十的十八次方個猴年之後,打出了以下內容「VALENTINE. Cease toIdor:eFLP0FRjWK78aXzVOw- m)-’ ; 8t …… 」驚奇的是,這胡亂敲打出的前十九個字母,正是莎士比亞的劇作《維洛那二紳士》(The Two Gentlemen of Verona)的第一行──VALENTINE: Cease to persuade, my loving Proteus。

在想到大寫鎖定鍵可能「碰巧」暫時遭到鎖定之前,我在思索的是那九個大寫字母。當然啦,四十二百京(編按:quintillion,即十的十八次方)是個相當龐大的數目,但平均得花上這麼久的時間才能等到這十九個字母以此特定的次序排列,並不代表這狀況不會在相較之下短得多的時間內發生。
也得承認,要想第一次亂敲就試出這樣的結果,機率實在小到難以想像,但並非不可能。意料之外的情事可能發生,也確實發生。以 DNA 配對為例,世界上是否會有兩個毫無瓜葛的人身上的 DNA 完全吻合?可能性微乎其微,但並非不可能。事實上,這機率僅僅只有十億分之一。


































-200x200.jpg)








