【性教育動畫下架公告】我們不夠謹慎，但不會停止討論。

• 文／雞湯來了 蕭子喬
  校稿／雞湯來了 陳世芃、張芷晴
  製圖／雞湯來了實習生 林佳宜
  編輯／雞湯來了 蕭子喬

剛剛在飯桌上，思琪用麵包塗奶油的口吻對媽媽說：「我們的家教好像什麼都有，就是沒有性教育。」媽媽詫異地看著她，回答：「什麼性教育？性教育是給那些需要性的人。所謂教育不就是這樣嗎？」思琪一時間明白了，在這個故事中父母將永遠缺席，他們曠課了，卻自以為是還沒開學。──《房思琪的初戀樂園》

多少家庭有國文、英文、數學課，甚至還有課外音樂課、籃球課、國際禮儀課，但卻唯獨沒有「性教育」課。孩子怎麼誕生的、到性徵發展、外表打扮、情慾萌芽……，「性」總被避而不談、模糊帶過。

究竟「性」怎麼了？為什麼這麼難啟齒？

沒被教過，也不知道該怎麼教小孩

缺席的性教育，正在一個個家庭上演中。兒福聯盟 2016 年「台灣兒童性教育知識調查報告」指出近七成（67.6%）家庭從未討論過「性行為」議題，超過一半（56.3%）從未討論過感情議題，將近一半（44.7%）家庭避免接觸 18 禁內容，三分之一（29.2%）家庭從未討論性生理發展的議題。

國內外探究父母為何不與孩子談論「性」，發現一方面源自保守的傳統觀念，一方面是多數父母在成長過程中，自己的父母很少，甚至從來沒有公開與自己談過性，自然而然就覺得這是一件羞於啟齒、不知如何談論的事情。

• 延伸閱讀：家庭如何影響一個人？、愛的方式不只一種，媽媽只是用她會的方法愛我

 六大常見家庭性教育迷思

台灣學者分析，父母排斥「性教育」可能來自以下幾個常見迷思：

迷思一：性知識孩子長大自然就知道？
快問快答：正確的性知識是靠學習而來的，網路性訊息泛濫而且容易取得，孩子自己隨意摸索有可能學到的是錯誤的。

迷思二：太早教孩子性知識，就是鼓勵孩子嘗試性行為？
快問快答：國內外研究報告指出，孩子懂得越多性知識，反而更懂得審慎自己的行為。

圖／轉載自原文章

迷思三：孩子一定要由同性別的家長教性教育？
快問快答：不一定！因為孩子可以從不同性別家長得到不同的知識及互動方式。

迷思四：父母必須有豐富的性知識，才可以談性教育？
快問快答：這是一個親子一起學習的好機會！用什麼都可以談的態度，讓孩子感到被傾聽、被接納，一起長知識。

迷思五：性教育只是老師的事？
快問快答：學校性教育授課時數仍不足！家庭是每個孩子「第一個」學習場域，在家落實性教育，很重要！

其實，性是人天生的本能，研究發現嬰兒即會藉由「撫摸」身體某些部位，滿足自己身體的探索慾。性不該是親子間的尷尬話題，而是愈早開始在家落實愈好。家庭性教育，並非真的很難，難是難在態度，關鍵在於跨出開口的第一步，用開放自在的心情談論。

不是只有性，家庭中各方面的議題討論

性教育是情感教育、家庭生活教育，也是品格教育，家庭性教育對於一個人的發展具相當重要的影響。性教育可以談論的面向很廣，由單純認識自我與生理「生殖器官」，到情感與人際的「情感、性別角色、交往戀愛」，再到保護自己和他人的「性騷擾、性侵害和家庭暴力」議題。完整的性教育可分為性生理、性病理、性心理、性倫理及性法理五個層面。

重要的是，家庭性教育並非要家長非常專業地教授性知識，而是用開放、可溝通的方式與孩子談論各方面的議題。台灣研究發現家長「教養態度」與孩子性知識程度具有非常顯著的相關，親子「經常溝通」的國小六年級學生在生殖生理知識、性騷擾及性侵害的認知知識均高於親子「不常溝通」的國小六年級學生。也就是說，親子之間越能開放談論各樣的議題，孩子對於自己的身體、保護自己的議題，了解程度通常也越高。

家庭性教育的三個入門策略

一、建立安全的溝通氛圍

研究發現，很多家長以為「談性」就要很專業、很嚴肅，其實並非如此。重要的是，讓家庭成為一個可以無話不談、可以一起討論想法意見的地方。學者建議家長掌握有問必答、掌握時機找話題（例如從影劇、時事出發）、分享父母自己的經驗…等，讓彼此的心更接近的方式與孩子藉由談心進行性教育。

• 延伸閱讀：迪士尼新童話告訴我們的事…

二、營造開明權威的教養風格

家長營造的家庭管教氣氛若是「開明權威」正向積極的方式，有助於子女培養正確性知識及性概念；相反的，家長若以「忽視冷漠、寬鬆放任、專制威權」等方式進行管教，那麼很可能從此關閉了孩子在家談性的勇氣（如本文開頭房思琪的故事），轉而從其他管道涉獵相關資訊。開明的性教育教養態度才能扮演子女的性解惑者、父母應主動增加與子女溝通的時間與內容。

• 延伸閱讀：「民主權威」最好？中西教養風格比一比

三、依據年齡選擇「談性」重點

從孩子還是個嬰兒，性教育就開始了！性生理（身體發展、性徵構造）、性心理（自我認同、性別氣質）、性社會（人際互動、性別角色）的議題，皆貫穿嬰幼兒階段至青少年，只是各階段側重點不同。下表是學者提出的各階段家庭性教育關鍵：

開口談性並不難，善用以上三點，開啟家庭的對話契機。不只是單純討論性知識，而是結合情感、人際、觀念與態度，讓性教育落實在每一天的生活中，讓家成為孩子最自在也紮實的安全堡壘。

參考資料

1. 兒福聯盟（2016）。台灣兒少性教育知識調查報告。
2. 林秀茹（2013）。親子談「心」說「性」落實家庭性教育。家庭教育雙月刊，45，59-67。
3. 高松景、晏涵文、劉潔心（2011）。高中生「全人發展」的性教育介入研究－以「生活技能」爲主。臺灣性學學刊，17（1），21-38。
4. 葉君玲、陳國彥（2012）。父母性教育教養態度與子女性知識關係之研究：以高雄市國小六年級學生為例。人文社會電子學報，8（2），68-98。
5. 余坤煌（1996）。國小學童家長性知識、性態度及對性教育看法之研究。臺灣性學學刊，2（1），11-24。
6. LARSSON, I., & SVEDIN, C. G. (2001).SEXUAL BEHAVIOUR IN SWEDISH PRESCHOOL CHILDREN, AS OBSERVED BY THEIR PARENTS.ACTA PAEDIATRICA, 90(4), 436-444.

本文與雞湯來了同步刊登，原文為家庭中為何不談性？3 個「家庭性教育」入門策略

• 文／雞湯來了 蕭子喬
  校稿／雞湯來了 陳世芃、張芷晴
  製圖／雞湯來了實習生 林佳宜
  編輯／雞湯來了 蕭子喬

曾有位中學生在情感教育的現場說「我們的教育一直跟我們說要避開恐怖情人，卻沒說如何當個好情人」。同樣的，性教育也是如此，時常倡導要「保護自己」，卻沒說怎麼「尋找自己、面對情感」。

被忽略的性教育：被跳過的健康課本，石頭蹦出來的孩子

「爸媽我怎麼來的？」
「就從石頭裡蹦出來的阿」

「這幾頁我們就先跳過喔，大家自己看」
「……」

兒福聯盟 2016 年調查發現，台灣中小學的孩子（調查樣本如註解）仍有將近三成（29.6%）曾遇過老師刻意跳過課本中的內容不談。

台灣學者 2009 年以問卷調查綜觀全國中小學（包含國小、國中、高中）性教育現狀，發現目前國中及高中職學校性教育的課堂教學仍偏重傳統的「性病預防」教育，對學生高度需求的性、愛、擇偶與婚姻等主動積極經營關係之「性心理、性社會」面向缺乏討論。

或許是因為許多師長年幼時在學校、家庭中都不曾有過「性教育」，使得許多師長不知該如何開啟這個話題，甚至害怕談了會不會反而讓孩子們太早接觸、太早嘗試。但其實研究發現，及早談、好好學，對於孩子而言對於性都會有更健康的態度。

研究指出，當學校性教育課程教得越詳細，教師教學技巧越好，且學生對學校性教育滿意度越高時，學生的性知識越佳，性態度越正向，相關生活技能的表現也越好。當家庭以越開放自在的教養態度談心也談「性」，孩子對於性知識的概念越完善、越健康。

更進一步分析，有學者以「前後測」探究實施性教育相關課程與活動的影響，發現性教育課程後對於參與者而言具有「立即效果」（剛上完課時，是真的和上課前不一樣），也具「延宕效果」（上完課兩個月後，仍把學過的東西留在腦子中）。

詳細而言，課程後及課程八週後參與者在性覺察度、性知識、性行為態度、拒絕性行為自我效能、交往生活技巧及性健康行為意向皆證實有效，且參與者認為確實能藉性教育課程活動，對人性、人生價值觀及愛等概念更加清楚。

• 延伸閱讀：家庭中為何不談性？３個「家庭性教育」入門策略

關於「性」，青少年關心的八個主題

從需求出發的教育，才能真正引起孩子學習動機，進而讓教學現場不只是師長單方的喊話，孩子的耳邊風；而是師生／親子的對話，深入孩子內心的體會與學習。台灣學者分析網路上青少年關於「性教育議題」的提問，從這些匿名提問網站，試圖了解青少年真正感興趣的話題有哪些。

研究結果可以整理出青少年上網提問的主要 8 個關注主題：性生理、性發展、自慰、避孕與懷孕、性別取向、兩性問題、性相關資訊、以及一般生活議題。

學者指出，這 8 大性教育主題的需求大致可和完整性教育主題對應，但不似完整性教育論者所提的那麼多；但是也不是禁慾教育路線者所提供的限制性資訊可以滿足。因此，以開放態度和孩子討論、讓孩子適度獲得解答，或許是性教育更符合「實際需求」的做法。

雖然此學者是以國外的完整性教育課程大綱、禁慾教育大綱為對照，但我們仍可反思此架構與台灣教育現況是否也有些雷同之處。或嘗試將教育部提出性平教育架構進行對照，藉以借鑑反思。

親師生共學對話，開啟性教育的溫柔革命

教師可嘗試用更多元有趣的方式進行性教育

學者發現目前性教育的課程活動以單向講述、缺乏互動式課程活動，是參與者對於性教育滿意度低的重要因素之一。教師可藉由學生感興趣的媒材，嘗試以設計思考、媒體融入等方式，避免單向講述、標準答案的教學，讓教學現場成為師生都能分享意見、融入參與的體驗學習環境。

家長可透過影劇媒材與孩子討論經驗與觀點

孩子們對於性的疑問，比我們想像得早、問題也比我們想像得多，家長可藉由和孩子共看電影討論劇情、共看新聞討論時事，來切入關於性這檔比較難啟齒的話題，接著家長可以分享自己的意見，也邀請孩子分享看法。可以「討論劇中人物／新聞中的角色」角度，將自己放在第三人稱的的角度中，降低自我揭露的害羞或尷尬感。

• 延伸閱讀：用童話《白雪公主》《小紅帽》《紅鞋》跟孩子開啟「性」的對話

參考資料

1. 兒福聯盟（2016）。台灣兒少性教育知識調查報告。
2. 曹恬珍（2018）。如何回應幼兒常見的性好奇行為。臺灣教育評論月刊，7（3）， 98－103。
3. 宋素卿、黃慧琪、林梅香、林秀純、陳慧郡、侯淑雲（2014）。推動校園性健康促進計畫歷程與成效之初探。臺灣性學學刊，20（1），27-54。
4. 高淑貞、黃以文（2004）。從網路性提問分析青少年性教育需求－他們究竟想知道什麼？中華輔導學報，16，1-34。
5. 林秀茹（2013）。親子談「心」說「性」落實家庭性教育。家庭教育雙月刊，45，59-67。

註解：

資料來源：兒福聯盟(2016)。台灣兒童性教育知識調查報告。
施測年份：2016 年
施測形式：實體問卷
施測對象：11-14 歲學生，有效樣本共 1479 份。
樣本描述：按台灣本島各縣市人口比例分層隨機抽樣，51.4%為男生、48.6%為女生；52.6%為國小五六年級生、47.4%為國中七八年級生。

本文轉載自 雞湯來了，原文為致老師與家長的一封信：我們一起練就面對性教育的勇氣

• 文／蔡宇哲，臺灣應用心理學會理事長、「哇賽！心理學」創辦者兼總編輯。

去 (2019) 年底所公布的國際學生能力評量計畫結果 (Programme for International Student Assessment, PISA) ，是在 2017 年進行測驗評量，主要評估項目為學生的閱讀素養，輔測數學與科學的素養，因此倍受科學教育社群關注。從結果看來，臺灣在這幾項素養的表現上都高於全球平均，看起來沒有太大問題。不過，卻有一項指標臺灣的分數高出平均甚多，甚至名列前茅，那就是害怕失敗指數 (index of fear of failure) 。臺灣學生在這項的得分是全球最高，這是怎麼一回事呢？

害怕失敗指數

研究是用以下三道問題的同意程度，來計算害怕失敗指數：

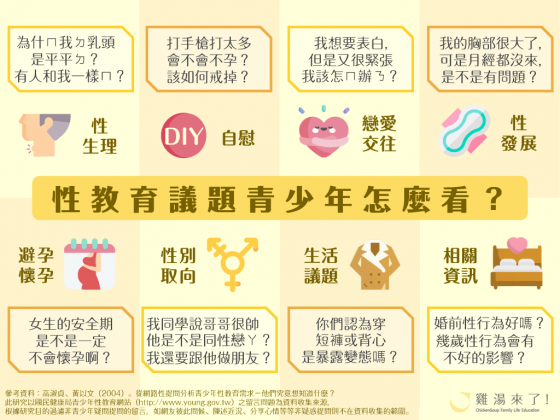
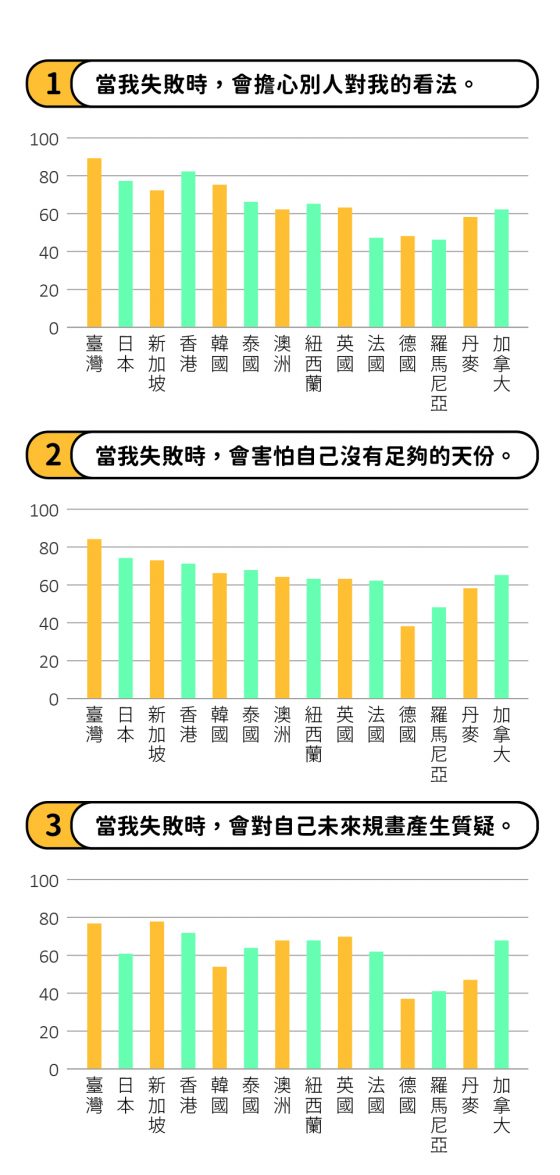
1. 當我失敗時，會擔心別人對我的看法。
   (When I am failing, I worry about what others think of me.)
2. 當我失敗時，會害怕自己沒有足夠的天份。
   (When I am failing, I am afraid that I might not have enough talent.)
3. 當我失敗時，會對自己未來規畫產生質疑。
   (When I am failing, this makes me doubt my plans for the future.)

除了計算之後的害怕失敗指數高於平均值外，即使是看各題得分也很高，都傾向害怕失敗所帶來的後果。看到這個結果似乎不太妙，會有一種「臺灣學生是全球最玻璃心」的結論，但筆者建議可以把這項結果當成一個警訊但不需要太過於悲觀。

對失敗的看法與學生本身的能力無關，而由獲得高分數的國家有很多來自亞洲這點來看，或許文化上本來就存在差異，像是新加坡與日本也都名列前茅，但並不代表這兩國家的學生特別玻璃心吧。況且，只有三道題目，筆者認為並無法完整評估學生對於失敗的態度，頂多是呈現一個面向。

想不害怕失敗，或許得先有成長型思維

雖然前述說了不需要太悲觀與在意，但仍可提供教育工作者作為參考與自省，畢竟學生太過於害怕失敗而不願意去挑戰並不是件好事。況且人們常會說「失敗為成功之母」，教育的目的應該是希望培養學生成為不畏艱難、不怕挑戰的人。

那要怎麼樣的人才會從失敗中學習成長，而不是一蹶不振呢？史丹佛大學 (Leland Stanford Junior University) 心理學教授杜維克 (Carol S. Dweck) 提出一個很重要的概念，就是需要有成長型思維 (growth mindset) 。

認為自己在各方面一直是可以成長的、遇到困難會認為有挑戰性而勇於嘗試、遭遇挫折不會放棄，會尋找其它可能成功的方法，這就是成長型思維的人所表現出來的樣子。與之相反稱為固定型思維 (fixed mindset) ，這樣的人會認為自己的能力是固定的，因此遇到新的困難會不願意嘗試，當遭遇挫折時也會很快就放棄，認為自己無法解決。杜維克教授認為，成長型思維的人能忍受困難、找出工作意義，長期下來比較容易進步，也就比較能夠成功。

過程決定方向，方向造就思維

那這兩種不同的思維模式是怎麼形成的呢？可以從一個研究的過程看出端倪。實驗找來一群孩子，先讓他們做簡單的作業，完成後會對一部份的孩子稱讚他「本人」，例如：「做得太棒了，你一定很聰明。」；對另一部份的孩子則稱讚他的「過程」，例如：「做得太棒了，你一定為此付出很大的努力。」

接著讓他們自由選擇第二輪的作業，結果發現，被稱讚「聰明」的孩子大部分都選擇了簡單的題目；相反地被稱讚「努力」的孩子則超過九成都選擇困難的題目。也就是說，如果人們注重的是孩子在過程中的努力，會讓他比較願意去嘗試有挑戰性、難度比較高的任務，培養出成長型思維；相反地如果只將結果連結到他本人的才能，就比較會為了維持同樣的好成績，而避免去挑戰與冒險而成了固定型思維。

這兩種思維的差異不僅在孩子身上，在醫學生及職場工作者的研究也都發現類似的結果。題目之一為「當我失敗時，會害怕自己沒有足夠的天份。」這樣把成功與失敗直接連結個人天份的想法，正是固定型思維的展現。因此，從這份結果來看，可以思考的是：教育過程是否讓學生關注過程而不是結果？

找出不害怕失敗的勇氣

筆者一直認為，科學教育是最好的成長型思維養成。試想，一個科學實驗的形成在於觀察、假設、驗證與預測，最精華的部份就在於前半段的過程。因此，在教學當中需強調過程的重要性，讓學生細緻地去理解與體會過程中的細節與難處，而不是去強調用高科技、很特別的研究方法所做出來的驚人結果，才不會讓學生誤以為結果才是最重要的。

當然這概念說來不難但實際執行上並不容易，過去幾年筆者負責帶領幾組大二的學生進行心理學實驗，都會向學生事先說明實驗過程中一定會經歷失敗與挫折，甚至最後也不會得到預期的結果，但這些都是很正常的現象。實驗重要的是過程而非結果，即使最終結果與假設不同，也是很好的機會去探討過程是否有偏差及其它可能原因，這才是科學實驗課程想要帶給學生的體驗。

不過礙於進度與時間有限，學生常在沒得到預期結果後就得倉促完成報告，後續的討論與再驗證的部份沒能有足夠時間進行，以至於學生無法領會到科學研究的醍醐味，只記得曾經做了一個沒成功的實驗，有點可惜。或許，許多教學現場的老師們也都面臨類似的難處吧。

用素養翻轉科學教育

108 新課綱強調的科學素養方向是正確的，嚴峻的少子化是危機也是轉機，讓老師們可以有更多的心力讓學生體驗科學的過程，而不是去背誦公式與各種科學結果。科學教育可以是「軟硬兼具」的，讓學生培養科學素養的同時也塑造了成長型思維，兩種實力都能夠在同一個歷程中成長，如此的教學改變是值得嘗試的。

〈本文選自《科學月刊》2020年 2 月號〉

在一個資訊不值錢的時代中，試圖緊握那知識餘溫外，也不忘科學事實和自由價值至上的科普雜誌。