本文轉載自中央研究院研之有物,泛科學為宣傳推廣執行單位。
- 文/採訪編輯|郭雅欣;美術編輯|林洵安
後量子密碼學標準化競賽
為了迎接後量子密碼學時代的來臨,美國國家標準與技術局(NIST)自 2016 年起舉辦「後量子密碼學標準化競賽」,吸引了來自全世界的團隊參賽一較高下,在這場競賽取得最終優勝者,將成為新一代的標準化密碼系統。最近,中研院資訊科學研究所楊柏因研究員的團隊以名為「Rainbow」的密碼學系統,通過了第一、二輪的考驗,於 2020 年成為進入決選的七組決勝者之一,距離成為世界標準,只剩一步之遙……

不論是網路購物,還是網路銀行的交易,我們在網路上的一舉一動,都依賴著嚴密的加密系統,保護我們的隱私不讓駭客從中盜取,守護我們的資訊安全。然而隨著量子電腦的發展,現行的加密系統卻面臨被破解的威脅。(有關目前的加密系統,請見研之有物另一好文〈量子電腦到底有多霸氣?即將引爆終極密碼戰?!〉)
因為當前加密系統的根基,都是一道複雜的數學難題,而主流的公鑰加解密系統,包括 RSA 加密演算法、橢圓曲線密碼系統,背後的數學難題複雜得讓古典電腦一籌莫展,卻正好是量子電腦最擅長解決的問題型態。
這些數學難題的答案,皆可轉化成週期性的結構。理論上,只要找到答案的週期,量子電腦就可以「較為輕鬆」的破解問題。
怎麼做?量子電腦的每個量子位元的數值是以機率呈現,意即每個位元會有一個最高機率的數值,代表這個位元最可能的數。研究者可針對以上答案具有周期性構造的數學函數,構造出相應的量子組態,使量子位元最高機率數值之間的差距,恰恰就是原本函數週期的整數倍 (例如:函數的週期是 4,量出來的差距可能是 4、8、12……。)接著,研究員只要測量這些差距,就能反推出函數的週期,破解古典密碼學加密系統所仰賴的數學難題!
密碼界的華山之巔
幸好,加密系統不只一兩種,這就好像武俠小說中總會有武當派、峨嵋派等,各種派別都有自己的獨門招式,加密系統也根據數學難題結構分成好幾派,除了當紅的 RSA 加密演算法、橢圓曲線密碼系統外,還有晶格、偵錯修正碼、多變量二次函數、雜湊函數及超奇異橢圓曲線同源等等。
為了因應量子電腦即將引爆的終極密碼戰,美國國家標準與技術局(NIST)自 2016 年起舉辦「後量子密碼學標準化競賽」,就如同一場武林大會,要找出能夠抵禦量子電腦的武林盟主,做為後量子密碼學時代的新標準。不過最後的標準至少要有兩個,分別用在數位簽章和加解密,所以與賽者也就很自然分成兩組。
武林大會的英雄帖一出,自然吸引了全世界的密碼學高手前來較勁,而中研院資訊所研究員楊柏因也是其一——他組了一個團隊,以 Rainbow 演算法參賽。在多變量二次函數這個派別,楊柏因也算是長老了,這一派的獨門絕技,就是多變量二次函數這個數學難題,也是楊柏因長期投入的主題。他和團隊也殺進了這場武林盛會中,而 Rainbow 這個難題的核心,是要解一個多變量方程組,其中包括 100 個變數,64 個二次方程組。
多變量二次函數問題的答案,沒有週期性結構,不是量子電腦擅長的難題,因此在後量子密碼學時代也能擁有很好的安全性。
兩階段廝殺:先攻擊,後防守
武林大會的第一場比武是個大亂鬥── 69 組參賽者提出的演算法,必須接受彼此的攻擊,如果被破解,代表安全性不夠,在這個階段就會被淘汰。楊柏因形容:「過程很像練蠱,最強的才能從甕裡爬出來。」2017 年 12 月 21 號公布這 69 組演算法後,雖然緊接著美國的聖誕節,但才短短幾天,就有不少演算法被破解,「大概阿宅是不過節的。」楊柏因笑稱。在一番廝殺後,Rainbow 順利通過考驗,成為進入第二階段的 26 個參賽者之一。
第二場比武要看的則是演算法的性能。一個派別的武功如果到了深山或森林等特殊環境就難以施展的話,那便無法成為武林盟主。同理,NIST 要求晉級的團隊將自家演算法在一般電腦、計算能力較弱的微處理機、硬體晶片上,都要能順利運作,而且效果不能太差。楊柏因解釋:「我們在這階段要做的是,在能保證 Rainbow 安全性的情況下,找出讓它跑得最快的參數。」
事實上,通常密碼系統的複雜度都是可大可小的,所以一個跑得比較快的演算法,相當於可以修改成跑得跟其他演算法一樣快、但更安全的演算法。
在現在的密碼學上,速度基本上可以等同於安全性,效能愈高相當於實用上安全性愈好。
第二階段的比武仍舊沒有難倒 Rainbow,一路過關斬將,Rainbow 成了七個有資格站上決選擂台的候選者之一。此外,在中研院資訊科技創新研究中心,周彤助理研究員所屬團隊提出的 Classic McEliece 也和 Rainbow 一樣是 Finalist。在七組 Finalist 中,中研院就佔了兩組,整體表現可說是相當不錯呢。
雨過天晴見 Rainbow
Rainbow 晉級的過程並非一帆風順。Rainbow 演算法的關鍵部分,被來自中國的的美籍學者丁津泰教授申請了專利,當楊柏因要組隊以 Rainbow 參賽時,曾詢問丁教授是否同意「如 Rainbow獲選,將免費釋出專利」。丁教授第一時間並沒有答應,後來楊柏因總算說服他如果Rainbow 獲選,將放棄專利營利。
密碼學上沒有什麼是非你不可的,換句話說,一旦 Rainbow 包含了一個沒有被釋出的專利,這個演算法幾乎不可能被選上。
另一個插曲發生在第二階段快要結束時,有人提出了一個以前就有的、針對 Rainbow 的攻擊的新研究,對方表示這個攻擊比楊柏因的團隊認為的更有效一些,楊柏因說:「我們重算了一遍,對方說的沒錯,但其實即使照著重算的結果,對我們的演算法造成的影響也還好,只要小小調整一下參數即可。」後來楊柏因重新提交修改的系統給 NIST,有驚無險的過關了。
強敵:晶格演算法
晉級最後一階段的除了 7 個候選團隊,另外還有 8 個備選團隊。總共 15 種演算法中,就有 7 種是「晶格派」的。數位簽章的三組決選者,除了 Rainbow ,另兩個都是晶格派。晶格通常指的是物質內原子的規則排列,但在此處指的是一個空間中向量構成的離散加法群。而「晶格派」背後的數學難題,則與空間中的向量有關——若在一空間中有 N 條向量,要如何從這些向量彼此的加加減減中,得到最短的向量?只要向量夠多,這個難題一樣複雜的讓古典電腦一籌莫展,而且,還不像 RSA 演算法一樣可以轉換成答案具有週期性結構的問題。
楊柏因承認,以目前後量子密碼學的發展狀況來說,晶格派是顯學,原因在於以晶格演算法產生出的公私鑰、密文、數位簽章等,長度約是現行的 RSA、橢圓曲線密碼系統的十倍左右。相較之下,Rainbow 所產生的公鑰長度是現行的數百倍之長,這也是 Rainbow 所屬這個派別最主要的弱點。
儘管有這樣的弱點,但 Rainbow 卻很適合運用在根憑證的數位簽章與驗章上,或是用在 CPU 的內碼微程式更新這類應用。這一類的過程不需要時常傳送公鑰,所以公鑰長一點也無所謂。而 Rainbow 在數位簽章與驗章的速度上,在候選系統中都是最快的。
公鑰長度很長是 Rainbow 的主要缺點,
不過它的簽章和驗章都是最快的。
Rainbow 的用途:數位簽章
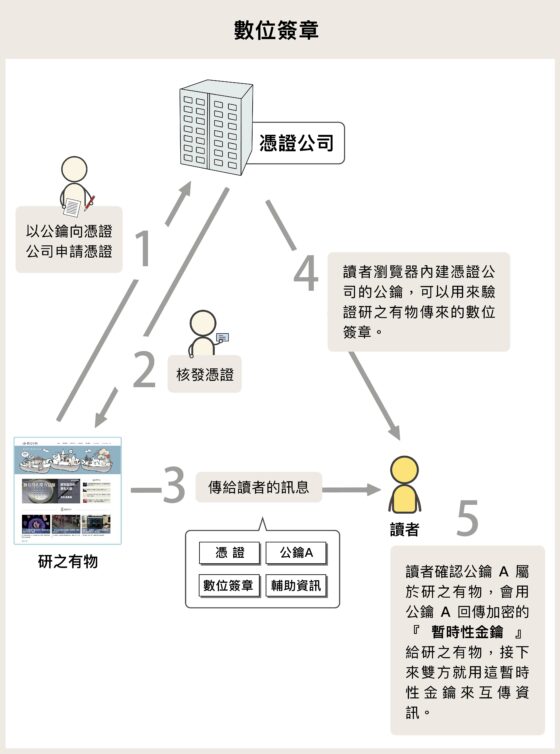
數位簽章(digital signature)在資訊安全上的重要性,並不亞於公鑰加解密。舉例來說,當我們在「研之有物」的網頁上買書時,除了不想讓我們的個資在與「研之有物」傳遞時被駭客獲取外,我們還得確定正在使用的網站,真的是「研之有物」,而不是駭客隨意建造的假網站。
為了讓前來購物的消費者安心,「研之有物」必須向第三方的憑證公司申請憑證,也就是請憑證公司證明「這個網站真的是我們,安啦!」「研之有物」必須提供自己的資料、自己的公鑰給憑證公司,憑證公司確認後,就會在「研之有物」的公鑰上簽一個數位簽章,就好像蓋個印章一樣。這個數位簽章只有憑證公司能簽得出來,其他人偽造數位簽章成功的機率極小,只有2 的 128 次方分之一!
消費者使用的瀏覽器中,則內建憑證公司的公鑰,這個公鑰可以辨認數位簽章(驗章),一旦辨認成功,代表「這個『研之有物』網站是憑證公司驗證過的,係金ㄟ!所以使用者可以安心購物囉。」
憑證裡的數位簽章可以認證網站的真實性,
保障使用者的資訊安全。
「NIST 曾說過,公鑰加解密與數位簽章會分開選擇,而(兩個組分別)決選出來的優勝者可能不只一個團隊。」楊柏因說。即使 NIST 選擇了以晶格為本的數位簽章系統 Falcon 或是 Dilithium,也大有可能讓 Rainbow 一起獲選。在數位簽章上的優異速度,可能成為 Rainbow 最終獲選的優勢。而楊柏因也開始「超前部署」,他正打算和資訊工程專家合作,準備嘗試將 Rainbow 放入實際的網路應用中,測試看看應用上會不會產生問題。「Rainbow 一旦成為新的標準,我們馬上就會需要這些東西。如果我希望 Rainbow 被選上,應該準備這些實作上的支援。」楊柏因說。
Rainbow 最後是否真的會成為世界標準?「謀事在人,成事在天。」楊柏因對此表現得很輕鬆,他說:「Rainbow 在簽章和驗章的運作表現數據確實最佳,但決定權還是在 NIST 手上。」身為盡責的研究者,「我會繼續我的工作,包括繼續研究 Rainbow 的安全性、測試 Rainbow 的實際應用狀況,其他的,就看 NIST 吧!」
事實上,楊柏因也加入了另一個團隊:NTRU Prime, 這一隊是屬於晶格派,而且不是七組最終候選者 (Finalist),而是八組備選者 (Alternate) 之一。他們在競賽中的地位相當於打入敗部,正在苦苦掙扎力爭上游。同樣的,他對此表示,盡力之後,就看老天爺 (NIST) 賞不賞光了。