via faungg’s photos
作者:阿捷〈捷學的哲學 〉
日常生活中,我們談及或接觸到的事物,譬如自然景物、生物、人造的物件……我們都會承認它們存在。它們的存在是那麼顯然,我們幾乎不會懷疑它們是否真實存在、只是腦裡虛構的事物。
為什麼?這很大可能源於我們可以直接觀察到(可以直接看到、摸到)它們。但科學理論裡,許多科學家提及的東西,譬如基因、電子、力場、光子等等,我們都不可以直接觀察到它們。那麼,我們如何肯定它們真正存在呢?
有人可能說:我們還是可以觀察到它們啊!譬如電荷,我們可以從安培計裡看到有多少電荷在流動。但請想清楚,當你在實驗室裡用安培計測試電流,透過安培計報告那裡有多少電流通過時,你並非真正見到有電荷在流動,你只是見到安培計裡的數值,然後才報告那裡有多少電流。
當代科學理論提到的許多東西都是不可直接觀察,雖然科學報告裡描述到它們像是可被直接觀察似的,譬如「兩個粒子現在正碰撞」、「不同的基因在重新組合中」……但嚴格而言,這些報告有誤導成份,科學家不可能真的觀察到兩個粒子在碰撞,他們只是透過各類儀器、數據,間接地推測這些東西如何活動。
讓我們把這些科學理論所假設的,卻無法直接觀察的物件,稱為「理論存有物」(theoretical entity),譬如粒子、力、波、電子、場等等。同時,我們把稱謂這些理論物件的名詞稱為「理論名詞」,例如「粒子」這詞是理論名詞,它稱謂粒子這理論存有物。
科學實在論:理論存有物真的存在嗎? 現在問題來了:我們能否用證明日常事物存在的原則,證明這些理論存有物存在?答案似乎否定。因為這些理論存有物無法直接觀察,我們不能用相同的原則──如果我們能夠直接觀察到某個東西,則這個東西是真實存在──推論它們存在。
雙縫實驗中電子真的像子彈般真實存在嗎?via universe-review.ca
假如你開始懷疑理論存有物的真實性,恭喜你,你已正式踏入科學哲學的領域。
有些科學哲學家認為理論存有物是真實存在。他們的想法是:如果我們相信科學理論為真,而理論存有物是科學理論所假設的東西,那麼我們應該很自然地相信它們存在才對。譬如,我們相信電子理論為真,那麼我們應該很自然相信電子存在,否則一方面相信電子理論為真,另一方面卻否定電子存在,豈非矛盾?
上述的想法可以寫成如下的論證:
(1) 如果某個科學理論為真,則這理論所假設的理論存有物是真實存在。
(2) 這些科學理論為真。
(3) 所以,這些理論存有物真實存在。(根據1,2)
這個論證是確當的(valid),我們質疑這個論證,只可以質疑它的前提。
有些哲學家反對(1),即使科學理論為真,也不代表理論存有物真實存在。哲學家羅素就反對(1),他的進路是:我們可以透過某種重寫的方式,使得這些本來需要假設理論存有物存在的理論,變成不再需要這些假設。
譬如,現假定電子理論為真。羅素認為,我們可以把理論裡假設電子存在的描述或內容全部進行改寫。改寫後的新理論,或是完全不需要使用到「電子」這理論名詞,或是理論裡照樣有「電子」這理論名詞,但它只是某種形式定義,並無真正指涉事物(如電子)。羅素相信,通過這種重寫,即使科學理論為真也好,它根本不需要假設這些理論存有物存在,因此也就不能推論出它們真實存在。
羅素的任務:重寫科學理論真的可能嗎?via pinterest
有些哲學家反對(2)。當這些哲學家反對(2)時,他們關注的是科學理論是否反映著世界的真實面貌。他們大多認為,當我們說一個科學理論為真,這變相承認它描述了世界的真貌,譬如電磁學理論告訴我們有多少電荷在電線裡流動,假如電磁學理論為真,電線裡便真的有電荷流動。
但反對(2)的哲學家認為,無論這些理論多麼有用,預測多麼準確、可以透過各種實驗去保證它們有某種合理性也好,這些理論只不過是人類理智的工具,它們並不描述世界的真實面貌。我們可以用一個誇張或嚴厲的說法表述這想法:科學理論並不配有「真」或「真實」的名號。
譬如基因工程逐漸變得和製造鋼鐵一樣普遍平凡,但這些哲學家會說:不要被騙了,不要以為真的有一串串很長的胺基酸分子在串連一起。當生物學家用金屬線或彩色球建構基因的模型,這些模型可以幫助生物學家更仔細思考生物學的問題,去發展更新更有用的微型科技(microtechnology),但不代表它反映事物的真實圖象。
這就是說,科學理論只是我們的模型工具,我們可以建構各式各樣的模型工具去解釋、預測、發展科技,但我們不能說這些模型工具真實地描繪世界。也許,讀者會問:這種說法有道理嗎?
基因只不過是模型? via kastglows.ca
我們可以嘗試用以下例子回答:我們能夠用滑輪、槓桿、滾球軸承、法碼等,做個經濟模型。重量代表貨幣供應量、角度傾斜度代表通貨膨漲率,而天平盤上的滾球軸承代表失業工人的數量。當貨幣供應的重量減少,通貨膨漲率的角度便會降低,而天平盤上代表失業工人量的滾球軸承便會增加。在這個模型裡,我們可以有正確的輸入與輸出,但它只是經濟模型,幫助我們思考經濟是什麼回事,我們不會說通貨膨漲率就真的是那些角度的傾斜度。同理,一串串很長的基因模型只是幫助我們思考生物學的問題,不代表真的有像模型般一串串很長的基因分子結構存在。
伊恩·哈金論兩種科學實在論 通過上面的討論,哲學家伊恩·哈金(Ian Hacking)認為我們可以區分兩種科學實在論:存有物的實在論與理論的實在論。
存有物的實在論主張,許多理論存有物確實存在。存有物的反實在論則認為,理論的存有物都是虛構的,它們只是某種形式的邏輯建構,或是科學家的工具。又或者,比較不獨斷地說,我們沒有任何理由假設它們真正存在。
理論的實在論則主張,科學理論至少是以真理為目的,而真理則是反映世界的真象。當一個理論為真,就表示它反映了世界真實的一面。理論的反實在論則認為,理論頂多只是實用、可接受它有某種合理性,但絕不反映世界真實的一面。
哈金提到,理論的實在論與存有物的實在論並沒有必然的邏輯關係,你可以接受其中一者,但反對另一者。現在,我們可以看到四項選擇:
(一) 同時接受理論的實在論與存有物的實在論
(二) 同時反對理論的實在論與存有物的實在論
(三) 接受理論的實在論,反對存有物的實在論
(四) 接受存有物的實在論,反對理論的實在論
(一)可以算是堅實的科學實在論者。通常有一班稱為「工具主義者」的人支持(二),這些工具主義者認為科學理論只是思考世界的理智工具,所以理論中假設的理論存有物同樣是工具,並非真實存在。(三)是有可能的,譬如上述提到的羅素,他就是一個理論實在論者,但存有物的反實在論者。
至於(四),哈金認為也是有可能的,譬如,雖然我們沒有完備的電子理論描述電子,但我們有很好的理由相信電子存在。我們的理論常常被修改,而且為了不同目的,我們可以使用不同的電子模型理論,這些電子模型理論都不應被理解為反映了世界的真貌,或者正確地描述了電子的特性;但無論如何,電子的確存在。哈金更提出了一個宗教上屬(四)的有趣例子,他認為很多神父都相信上帝存在,但同時認為任何人類所構造出來描述上帝的理論都不可能是真的,因為人類無法真正了解上帝。
哈金這本書是非常好的科哲書 via cnstrctvsm
科學實在論只是哲學家的玩意兒嗎? 有些人聽到這裡,可能認為這樣的討論很無聊,只是哲學家的玩意兒。尤其是一些科學家,他們認為整個科學實在論與反實在論都是虛假的問題,沒有實質的意義,也對科學完全沒有影響,如同理查·費曼(Richard Feynman)的名言:「科學哲學對於科學的用處,如同鳥類學對於鳥的用處。」(Philosophy of science is as useful to scientists as ornithology is to birds)
我自己對這問題的回應是:不全對,也不全錯。科學哲學的問題確實只有哲學家會關注,科學哲學也對科學發展沒有影響。不過,即使如此,這也不代表科學哲學只是一種「無聊的玩意兒」。當我們嚴肅、認真地看待我們的知識,並作出最根本的反省──即使這是瑣碎無用的哲學反省也好──我們還是可以問「原子是否真的存在?」這樣的問題並沒有錯誤,即使問得愚蠢也好,它也是人類愚蠢得來最深刻、最漂亮的反省。
其實,科學界裡都會有實在論與反實在論的討論,不過主要針對的是個別理論,並非所有科學理論。譬如,在哥白尼時期,天文學家不願意相信哥白尼的日心說,他們堅信宇宙的中心是地球,雖然他們承認太陽中心系統有助於運算,但這不代表世界的真象。在一些時期,物質主義者(materialist)主張存在的事物都是由微小的物質所構成,他們相信原子存在,卻反對非物質的力場存在。到了現代,量子力學詮釋的討論中,也掀起了一些實在論的討論:我們應該說粒子的確有確定的位置和動能卻無法測知,還是我們應該說波包塌縮(Wave packet collapse)是它和人腦的某種活動效應。
不過,哈金提醒我們,這些個別理論的反實在論問題都可以藉由科學解決。譬如統計力學發明者之一詹姆斯·克拉克·馬克士威( James Clerk Maxwell),曾認為氣體並非真的由那些很細小、像軟皮球的東西所組成,這些東西只不過是模型,方便我們解釋溫壓效應。但當這個模型愈來愈能解釋物理現象,他便傾向實在論。在科學界,某種理論或理論存有物的反實在論者,最後因理論成果愈來愈出色而逐漸成為實在論者的情況十分普遍。
有些人可能因此主張,所有反實在論的問題都可以通過科學的發展解決。譬如,當弦論、黑洞理論變得愈來愈成熟,最後懷疑這些理論的反實在論者都必定要閉嘴和投降。不過,我認為,科學家和哲學家討論「實在論v.s.反實在論」,是兩種完全不同的層次。科學家討論的是某個科學理論是否足夠成熟、有很高的可信度、比其他理論為佳;假如答案是肯定的,它就屬實在論。哲學家討論的則是退一步的問題(後設問題):我們是否應該視科學理論為反映世界真貌的真實理論?
如果我們的立場傾向工具主義,便會認為科學理論再成熟也好,我們仍是無法確定它們是否反映世界真貌、沒法確定這些理論所假設的理論存有物是否真實存在。或者,我們應該更進一步地問,何謂「真實性」(reality)、「真理」(truth)、「真實存在」(really exist),如何回答這些問題,也將令我們遊走於實在論與反實在論之間。
我對科學哲學有興趣,是因為我中學時,從科普書裡認識到霍金理論有所謂虛時間的東西。數學家用√-1 定義虛數,虛數似乎沒有任何物理意義。如果說宇宙中存在著虛時間,它到底是什麼東西?它只是一個數學模型,可以方便我們進行預測、應用,還是反映了世界(時間)的真實一面?假如你對這些問題有興趣,那就表示你可能有興趣踏入科學哲學的討論裡。
Reference
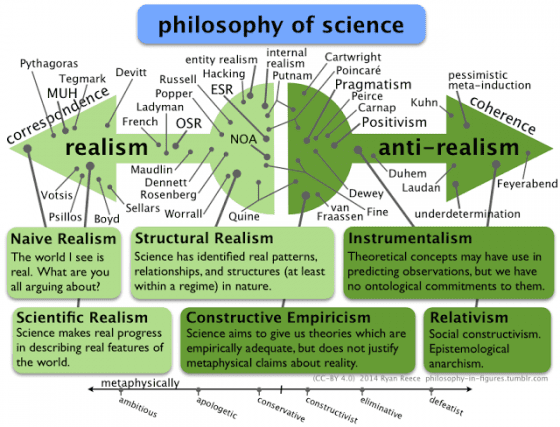
這幅圖簡介了幾個科學哲學的重要理論 via thumblr