小時候,我最喜歡 9 這個數字了,因為它似乎蘊含許多神奇的特性。我想給你看一個例子,請照著下列充滿魔力的數學指示:
- 想一個在 1 到 10 之間的數(如果不滿意,你也可以挑更大的整數並使用計算機)。
- 將這個數乘以 3。
- 然後加上 6。
- 把得到的數字再乘以 3。
- 如果你願意的話,把這個數字再乘以 2。
- 將這個數字的所有位數相加,如果是個位數,就停止運算。
- 如果是二位數,那麼將兩個位數再次相加。
- 專心想著你的答案。
直覺告訴我你正在想的數字是 9,對不對?(如果不是的話,你或許該回過頭驗算一下。)
是什麼讓 9 這個數字如此神奇?我們會在本章看到它的一些神奇特性,然後我們甚至會考慮有另一個世界的存在,在那裡 12 和3 的功能相等而且完全合理!
觀察 9 的倍數
9 的第一個神奇特性可以從它的倍數中看出來:
9、18、27、36、45、54、63、72、81、90、99、108、117、126、135、144⋯⋯
這些數目有什麼共通點?
如果你將每個數字各自的位數相加,似乎每次都會得到 9。
讓我們挑其中幾個來試試看:18 的各個位數之和是 1 + 8 = 9;27 是 2 + 7 = 9;144 則是 1 + 4 + 4 = 9。但是慢著,這裡有一個例外:99 的位數和是 18,不過 18 本身仍是 9 的倍數。所以我們得到下面這個重要結論,這件事你可能在小學就學過了,而我們稍後也會在這一章中解釋:
如果一個數字是 9 的倍數,那麼它的各個位數之和也必定是 9 的倍數(反之亦然)。
舉例來說,123,456,789 的位數和是 45(9 的倍數),所以這個數就是 9 的倍數。反過來說,314,159 的位數和是 23(非 9 的倍數),所以這個數就不是 9 的倍數。
整數的強大性質
讓我們用這個規則來了解前面的那個魔術戲法,並仔細檢驗其中的代數。你先想一個數字,我們稱之為N。乘上三倍之後你會得到 3N,在下一步變成 3N + 6。將這個數字再乘上三倍則是 3(3N + 6)= 9N + 18, 也就是 9(N + 2)。如果你決定要再乘上 2, 就會得到 18N + 36 = 9(2N+4);但不管有沒有乘上 2,你最後的答案都會是9 乘上一個整數,所以最後一定會得到 9 的倍數。(編按:這就是整數的強大性質之一,任何一個 a 倍數乘上任意整數,仍然還是 a 的倍數)
當你計算這個數字的各個位數之和,你一定會再度得到一個 9 的倍數(可能是 9 或 18 或 27 或 36),而且這些數目的各個位數之和必定為 9。
還有另一個我也很喜歡用的魔術戲法,它是前面那個魔術的變形。找一個有計算機的人,請他從下列四位數中挑出一個:
3141 或 2718 或 2358 或 9999
這些數字分別是 π(詳見第八章)的前四位數、e(詳見第十章)的前四位數、連續幾個費氏數(詳見第五章),以及四位數的最大值。
請他將所選的四位數乘上任何一個三位數,結果會是一個你不可能會知道的六位數或七位數。接下來請他在腦海中圈出答案中的任一位數,但不要是 0(因為它已經像是個圓圈了!),然後要他以任意順序將所有沒圈起來的數字唸出來,並且專心想著那個剩下的數字。你只要稍加注意,就可以成功地揭開答案了。
又是 9!
所以說祕密是什麼呢?請注意,能選擇的這四個數字都是 9 的倍數。
既然是從一個 9 的倍數開始,那麼乘上一個整數之後結果仍然會是 9 的倍數,因此它的位數和也一定會是 9 的倍數。隨著數字被逐一唸出,你只要將它們統統相加即可,被藏起來的那一個數字在加上之後能使總和變成 9 的倍數。舉例來說,假設他唸出 5、0、2、2、6 和 1,這些數字的總和是 16,那麼被藏起來的數字一定是 2,因為加上之後能得到最接近的 9 的倍數,也就是18;如果唸出來的數字是1、1、2、3、5、8,總和為 20,那麼隱藏的數字一定是 7,這樣才能得到 27;假設你將唸出的數字相加得到 18,他藏起來的是哪個數字?由於我們告訴過他不要圈選 0,所以缺少的數字一定是9。
謎底揭曉
但為什麼一個 9 的倍數其位數和永遠是 9 的倍數呢?讓我們來看看下面這個例子,當 3456 以 10 的次方項表示時,看起來如下式
3456 = (3 × 1000) + (4 × 100) + (5 × 10) + 6
= 3(999 + 1) + 4(99 + 1) + 5(9 + 1) + 6
= 3(999) + 4(99) + 5(9) + 3 + 4 + 5 + 6
= (9 的倍數)+ 18
= (9 的倍數)
運用同樣的邏輯,如果一個數字的位數和是 9 的倍數,則此數本身一定也是 9 的倍數(反之亦然:任何一個 9 的倍數其位數和一定是 9 的倍數)。
編按:任何一個整數,都可以寫成 9 的倍數+各個位數數字的和,如同上式第四行,因此只要各個位數數字的和是 9 的倍數,整個數字就會是 9 的倍數。

——本文摘自《數學大觀念:全面理解從數字到微積分的12大觀念》,2023 年 3 月,貓頭鷹出版,未經同意請勿轉載。















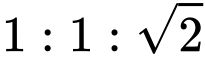 。圖/
。圖/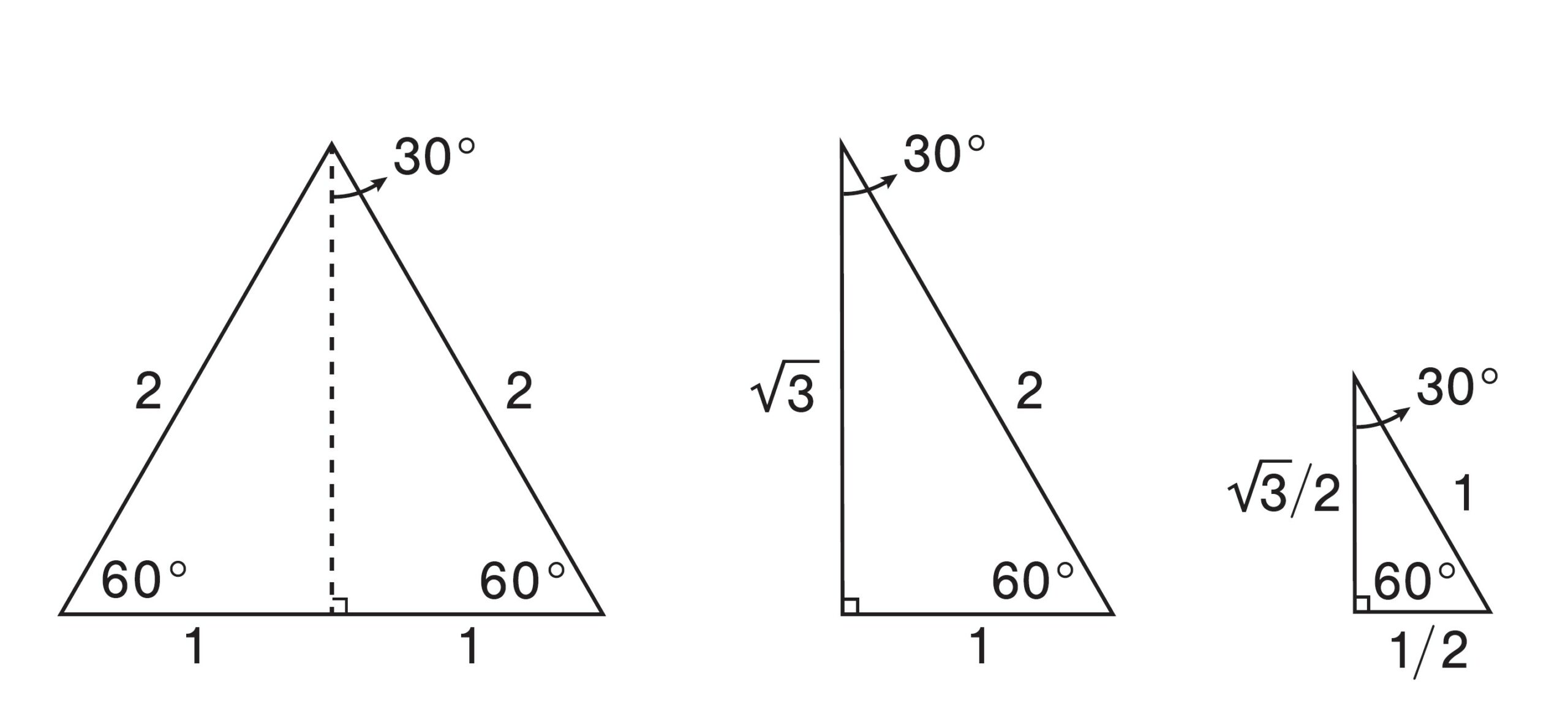
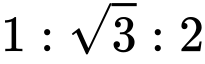 。圖/
。圖/