你是,這樣的人嗎?
- 你總是覺得,自己沒有別人說的那麼聰明。
- 你總是害怕,自己所擁有的才能或天賦,有一天就會消失殆盡、然後其他人就會不喜歡你了。
- 在感情裡面,你總是被拋棄的那一個,並且每次開始交往的時候,就時時刻刻在倒數計時你所殘存的戀愛。
- 因為青少年時期被霸凌的經驗,讓你對於人際關係和感情失去的信任,於是你把真實的自己藏起來,只用「假面」在過生活。
- 和伴侶分手之後,你很不意外的並沒有感到很難過,因為你早就知道:「如果你太一個人,他就不會很愛你了」,所以這次的分開對你來講殺傷力很小,但不知道為什麼,想起來的時候還是覺得有一種很悲哀的感覺——為自己的防衛感到悲哀。
前幾天收到了《再見凱薩琳》這本書問我是否能推薦,由於是《生命中的美好缺憾》的作者約翰所寫的書,想說應該蠻有趣的,於是就把他帶到花蓮去渡假。裡面的主角,就是擁有上面這些特色的人,沒想到……。
雖然帶這本書去花蓮,不過還是在回來台北的火車上才有時間真正的開始看,剛剛看完之後有幾個很複雜的感覺。基於許多原因,我覺得實在無法推薦這本書。不過,倒是有很多地方值得討論與評論的,所以我特別寫了一篇文章。
__________以下有雷__________
解析「再見凱薩琳」

一分鐘讀完這本書(谷X莫):這本書描述男主角天才兒童柯林和他的好基友哈桑利用暑假進行一段公路旅行的過程,對於柯林來說,這是一段走出失戀的旅程。這是他第 19 次和名叫「凱薩琳」的女孩分手,你可以想像你總是和叫「怡君」的女孩交往,但每個都最後都甩了你。而對於哈桑來說,這是一次逃避上大學的旅程,他已經多次休學,這次也想「照舊」繼續休學。他們在開始旅行之柯林後不久就遇到了女主角琳西以及存在感很低的女二卡特蓮娜(不是英雄聯盟裡面的那一個)。
柯林整本書都在研發他的「凱薩琳分手公式」,他想知道為什麼自己一直是被甩的那一個,因緣際會之下與哈桑一起到琳西她家打工,三人一起訪問她們家族事業體的員工,要作一本回憶錄之類的,因此產生了感情,柯林還很幸運地獲邀和琳西一起到她的秘密基地(一個洞穴)喝酒聊天。後來,哈桑和琳西的好友卡特蓮娜在一起、接著琳西的男友(也叫柯林)劈腿卡特蓮娜被抓包,最後哈桑與卡特蓮娜分手,琳西與主角柯林在一起(貴圈真亂 XD),柯林很悲觀得以為他們 4 天之後會分開(照他的理論預測)沒想到竟然沒有,大家幸福快樂、哈桑也準備去上大學了,故事結束。
整本書用了非常多冷僻的註解,包含不同的語言、柯林最喜歡的字母重組遊戲、一些你不知道也不會怎樣的歷史或者是科學知識、以及數學圖形和公式,不過這並不是我「不能推薦」的原因。一言難盡,下面簡單用六個小點解析這本小說,以及說說我個人的想法:
1.用科學「解」失戀
故事的主角柯林根本就是多年前的我呀,當時我也是歷經一場失戀,想要在各種論當中去找出預測分手最適合的數學模型,實際上也找到了一些看起來勉強可以用的模型(請參看《這才是分手の心理學》),但最終發現:
它們並沒有辦法拿來預測「真實」的戀情,因為……所有的模型都是化簡最後的結果,可是一段感情的「生生滅滅」需要考量的變數太多,我們不可能考量到所有的變數。就算把效果最大的變數考慮進去,其中的交互作用也複雜到無法用數學模型來表示。
2.主角柯林:亞斯伯格症?
老實說一開始在讀這本書的時候,覺得非常卡卡 der 凍茲凍茲,受限於他裡面跟文化有關的用字。我對於裡面許多讀起來覺得不好笑的諧音或者是拼字遊戲,感到很苦惱(跟陳澄波本人一樣感到很苦惱),並且嚴重的阻礙的閱讀,我想這個如果換成我們中文其他的一些諧音,可能會比較接近我們的文化,不過畢竟是翻譯書,也無法苛求阿(阿不然你來翻譯阿~)。
另一種可能是,或許我對於美國、阿拉伯、德國等等的文化了解很有限,所以真的不太能夠了解故事當中兩個主角哈桑和柯林開的一些玩笑。不過,我倒是很能夠理解柯林有點像是亞斯伯格症的特徵(當然,這只是我個人的猜測,畢竟作者也沒有設定他是亞斯),例如會專注在一些非常小的事情,而且有非常低的社會化能力,沒有辦法察言觀色、而且沒有辦法容忍不公平不正義的事情。如果你懷疑你是,可以參考 Baron-Cohen、Wheelwright、Hill、Raste 與 Plumb 等人(2001)「亞斯柏格成人量表」,由國內設計團隊 Re-lab 製作50題清晰易填的線上檢測。
3.基友哈桑:逃避型人格?
我覺得蠻特別的是,就是傳說中的「逃避型人格」的人(和逃避依戀有一些重疊,但不完全等同)(Johnson、Murray,2008;岡田尊司,2017a,2017b),人生所擅長的事情就是「逃避情緒」與「自我設障」。
- 「逃避情緒」:根據胡展誥(2017)的定義,長期逃避情緒的種「情緒殭屍」有幾種特徵──
- 問題解決至上:深信「情緒」是庸人自擾、毫無必要的阻礙物。
- 超理智:對每件事都只是理性分析利弊、評估成效,毫無情感成分。
- 說不出口:除了煩悶之外,無法清楚表達自己當下的情緒。
- 自我設障(self-handicapping):「什麼事都不做」來避免可能的失敗(就像你期中考之前會通宵打電動,這樣考差了就可以說「我只是因為不念啦,認真起來連我自己都怕!」;考好了更秋,「恁爸沒念都考這樣了,你們這些小嫩B!」)(Jones、Berglas,1978),有這款情形,掐卡0800-……。不過最讓我最感動的是,在故事的最後,他終於了解自己一直以來的逃避,並且嘗試要做出和以往不一樣的事情。
4.女主角琳西:情緒殭屍
在我看起來是一個不相信愛情、或者可能是逃避依戀(岡田尊司,2017a)的人。或許受到爸媽離婚的影響(Mustonen、Huurre、Kiviruusu、Haukkala與Aro,2011)、或許人生當中發生一些事情(例如求學時代曾經被排擠)(吳姵瑩,2017)而影響到他對自我的感覺以及安全感,她選擇把心鎖起來,不再對任何人付出真心,可是也因為這樣,她在和「另外一個柯林」(故事當中另外一個同名配角,身材魁梧)分手之後,沒有感覺到有任何的悲傷—— 然而,這才是最大的悲傷——那些自以為把感覺隔離開來就不會感覺到痛苦的人,實際上,也失去了快樂的可能。她把自己變成沒有任何感受的情緒殭屍(胡展誥,2017),卻也傷害了要進入她內心的人。
5.關於男女主角的感情
這本書當中,我覺得最可惜的是,對於男女主角感情的刻劃稍微少了一點,如果按照過往主角柯林的感情經驗來說,我猜想這段感情雖然在故事結束之前還沒有分開,但應該會走上他過往的「凱薩琳曲線」(柯林鑽研出來的定理,用來預測一段感情的生生滅滅,不過大部分都是悲劇收場),原因有兩個:
其實他們根本沒有真正非常了解彼此。會在一起,只是因為兩個人曾經在秘密基地黑暗的洞穴裡面,交換彼此的秘密、自我揭露(Self disclosure)。做了親密的行為(碰碰額頭),就好像很愛彼此的樣子,可能只是一開始的假象。
另外,柯林與琳西某種程度上都是自卑的人。根據我的了解,一個人的自卑不太可能在「瞬間」就有所轉變。雖然他們兩個人都體會到,自己對於其他人的不信任、對於感情的失望,也願意嘗試看看新的感情,不過,我認為他們真正的生命課題並沒有解決,所以這段感情看起來有一個不錯的開始,但我猜測應該結束不會太慢。雖然不是柯林自己的定理所預測出來的4天,但有可能不會超過40天或者是400天。另外,他們這樣的感情我們在心理學上面稱作「籃板球戀愛」(Rebound Relationship)(Brumbaugh、Fraley,2014;Spielmann、MacDonald與Wilson,2009;Wolfinger,2007),通常是指在分手之後不久立刻開啟的另外一段新的關係,當事人往往會和過去的極端感情作比較,尤其是柯林,一定會把琳西和他前面19個凱薩琳進行比較──然後發現,舊愛還是最美。
6.關於數學公式
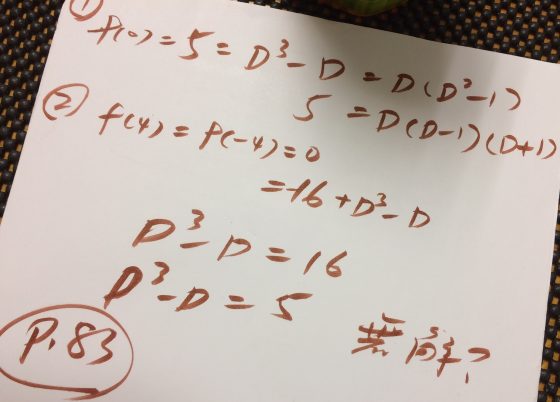
其實我覺得這是這本書最大的賣點,不過也是最大的敗筆。一開始我覺得會不會是我才疏學淺,沒有辦法真正理解公式,還拿出了紙認真的計算了一下,後來發現我可能真的資質駑鈍,完全無法理解這個天才兒童的想法。不過還好,這本書的最後面竟然有提供解答,真是讓我看得津津有味。看到後面的解答才突然想到,這個D根本不是常數,而是變數,難怪我會得不到解答。
不過我覺得非常可惜的是,作者在書當中所用的公式和裡面的劇情好像是截然劃分的兩個世界,作者並沒有在書中的19個凱薩琳分手的案例當中指出,他們是如何讓這些係數影響了彼此的互動,也沒有辦法說服我這幾個不同的係數他何以是最重要的係數。當然,作者在最後有提到,這個公式其實是他的數學家好朋友編纂出來的,而他自己的數學非常差,也難怪我們會發現公式和劇情之間有這麼大的隔閡,畢竟要用自己不熟悉的方式來串連劇情,其實很不容易。
真的存在所謂的「戀愛公式」嗎?
好啦,既然我曾經也想要找所謂的「戀愛公式」但為什麼我會覺得沒有辦法推薦這本書呢?
上面這個是柯林最終版本的數學公式,用來預測兩個人到底最後是誰會甩了誰,其中,y 如果越接近零(不論是正的還是負的),表示這段關係越接近分手,而 y 等於零的時候,就表示一段戀情的結束(或者開始)。這個曲線如果開口朝下,就表示是女性甩掉男性(以異性戀為例),如果開口朝上,就表示是男性甩掉女性。
柯林用了幾個不同的指標來建構這個公式(以下整理自書的 159 頁到 160 頁)
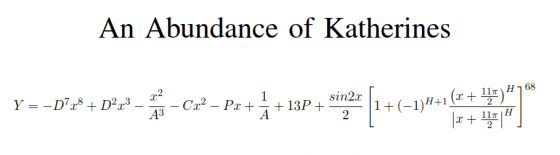
公式引自書中 p.240,由賴以威老師協助繪製而成。
- 年齡( A ) =[(男生的年齡+女生的年齡)/2]-5
- 人氣差異(C)=(女生的人氣指數—男生的人氣指數)/75,其中,人氣指數是介於 1~1000 的數字。在我的理解上,應該是指這一個人有多受到同儕或朋友的歡迎。
- 魅力差異(H)=(女生認為這個男生有多吸引她—男生認為這個女生有多吸引他),這個評估吸引力的分數會介於 0~5 之間,數字越大表示他認為這個人越省他
- 拋棄者/被拋棄者差異(D)=(女生習慣當拋棄者的機率-男生習慣當拋棄者的機率),由於是機率,所以括弧內這兩個數字應該都是介於 0~1 之間的數字。這個概念應該是,沒有人會一直永遠當拋棄者或者是被拋棄者,例如說,在 10 次戀愛當中,你大概有 8 次是當提出分手的那一個,那麼你的數字就是 0.8;如果你的前女友總是被甩的那一個(假設你是個男的),那麼她的數字就是 0,而這裡算出來的 D=0-0.8=-0.8
- 內向者/外向者差異(P)=(女性的外向程度-男性的外向程度),(唸的兩個數字以 0~5 分來估計,分數越高表示這個人越外向,越低表示越內向。

這個公式,可信嗎?
本書作者的朋友(也就是一個數學家)在書的最後面有交代這些公式的創作原理,不過就算我們還沒有看到公式,光是看這個設定可能就會有許多的問題:例如,一個人的內外向可以用單一向度來表示嗎?有沒有可能有人是同時內向又同時外向的人?上面這些要素真的涵蓋了所有交往的時候重要的條件嗎?
如果我們再仔細看這一個公式,會發現更多問題。在心理學上面,我們必須交代兩個數字相減的意義(其實這個和以往在做伴侶研究的邏輯是相符合的,有興趣可以參閱此文), 以及為什麼要除以某個數字、加上幾次方(可是書裡面都沒有交代),其實主要就是基於這點,沒有辦法推薦這本書。
雖然我理解這本書的初衷或許就是再告訴我們:愛情是不能夠用公式來預測的,不過,作為讀者的樂趣立場,以及心理學研究者,我還是比較希望他可以去解釋每一個係數的形成原因以及結果,在這本書的最後面,作者的朋友(也就是那位協助他的數學家)附錄給的那個網站,裡面 John Gottman 提到的一些公式也和作者的這個公式完全不一樣(至少使用的要素不同),所以如果說是參考來的,我覺得也有一點不太一致(有興趣的可以參考這幾篇論文)(Bakeman、Gottman,1997;Gottman,2014),或是以威老師的這篇文章。
另外,柯林的公式其實離目前親密關係的研究,相去非常遙遠(沒辦法,畢竟他只是一個學生,也不能夠太苛求他)。
舉例來說,我讚同有些人在感情上面就是習慣當拋棄者或者是被拋棄者,也就是 D 這個數字的確有可能會坐落在一個常態分配上面,的確是一個合理的參數;其他的數值我覺得也挺合理的,不過有2個最重要的參數,是目前研究當中發現效果量很大的:
- 自我揭露:其實就是你講一點你的秘密,我一點我的秘密,也就是男女主角在秘密基地裡面做的事情。許多研究顯示他是會增加兩個人之間親密感的好方法。但在柯林的公式中,並沒有考慮到此因素
- 面對衝突的時候的溝通:然而,上面這個要素通常只會預測兩個人在一起的速度,而沒有辦法預測兩個人「是否能夠快樂的在一起」。其實如果你觀察那十九個凱薩琳,你就會發現同樣一件重要的事情就是,柯林從頭到尾沒有真正學會去處理溝通這件事情,這也是為什麼我預測他其實和琳西也不會太久哈哈哈。
然而,在柯林上面最新的(而且看起來很酷炫的)公式當中,沒有把這兩個重要的條件擺進去,是我覺得非常可惜的原因,某種程度上也解釋了,為何後來他的公式沒有辦法預測他們兩個人是否會在第四天分手。琳西喜歡他這個公式,充其量只是認為看起來很酷而已,以及他覺得兩個人有一種同病相憐的怪咖的感覺(其他還有很多預測分手的因子,柯林都沒有考量,有興趣的人可以參看下圖)(Le、Dove、Agnew、Korn與Mutso,2010)。

預測柯琳戀的結局
換言之,這樣的結局只說明了幾件事情:
- 兩個人或許(在漆黑的洞穴裡面)卸下了一些自己的心房,但仍然在感情最開始的交換秘密的階段,可能表面上看起來很甜蜜,但能不能夠撐過後面的風雨就不得而知了。
- 我認為很大一種可能是,這個新的對象也會走向前面19個凱薩琳一模一樣的結局——在柯林還沒有學會如何好好的人際交往以及溝通之前。
- 這兩個人之間會互相吸引,我猜還有一個重要的因素是來自於,他們對於感情的看法都比較悲觀,而這個悲觀形成了某一種吸引力,讓兩個人有一種「同病相憐」的感覺。不過,根據我的了解,對於關係的悲觀,其實是來自於對於關係的缺乏安全感,以及低自尊。就像是兩個男主角在吵架的時候,你可以很明顯的看到,這兩個大男孩,其實都是很沒有自信的人。在這樣的情況下開始一段戀情,可能會有許多辛苦以及需要調整的地方。
如何走出一段失戀
如果有人也正經歷一段失戀,然後正在想要怎麼樣才能夠走出來,那麼這一本書將會是一個很好的示範。
等等,先別高潮,這並不是說本書教你如何走出失戀,也並不是因為當事人用了什麼神奇的招式,使得他得以走出這個悲傷,而是幾乎所有的人都會用自己所習慣的方式來面對悲傷(例如,這個天才兒童柯林習慣的方法是不斷地重組字彙、不斷地專研他所謂的定理)——這個事情本身沒有太大的幫助,真的。後來真正發生效果的,或許是在這些「重複」當中所產生的一些新奇的事情——去打獵山豬、被蜜蜂咬、被別人踢睪丸、進入一個大工廠的倒閉事件、訪談那些與自己年紀相去甚遠的老人們、在一個漆黑的洞穴裡面喝著純釀威士忌、和好基友進行一場看起來似乎沒有盡頭卻一開始就走到盡頭的公路旅行等等。
其實你可以跳過上面一段,那是寫給文青看的哈哈。
想要變好?你只要跟柯林一樣找下一個對象在一起就好了。研究發現,相較於上面這些狗屁倒灶的事情,找到下一個對象,往往是走出失戀,效果最大的方法。有新伴的人比起沒有新伴的人,感到更幸福、更有自信、前一段感情的殘渣越少、越不會與前任藕斷絲連(Brumbaugh、Fraley,2014)。雖然我很不想承認(因為這樣似乎顯示我們這些心理學家的失戀介入好像沒什麼用),不過這的確是事實。
其實你也可以跳過上面這一段(好啦但是這一段不要跳過),因為我漸漸發現,如果我們用數字來測量,當然可以很明顯的看到「認識新的對象」、「和新的人在一起」有正向的影響,例如當事人可能會對自己的看法比較正面、不會再和前任情人糾纏、不會再反覆想起前一段感情當中的起伏、比較少的失落等等,但是——有些東西是無法用數字所測量出來的。例如,你在失戀過後一直到遇到下一個人之前,這段時間心情的起伏、對於自我的整理、因為失戀促使你去做的一些愚蠢或者是從來沒有嘗試過的事情,其實都會成為你人生當中很重要的一部分。
真正重要的並不是「有沒有走過失戀」、 是否真的和心中的「那個凱薩琳好好、完整的說再見」,而是在離開前任之後,你有沒有展開另外一種,和以往截然不同的人生;有沒有辦法接受自己只是一個平凡人、接受其實自己真的「沒有很完美」的那種失落。
這個沒有辦法用數字或用統計來測量的、屬於你的故事,才是對你來說,最重要的小事。
延伸閱讀
- Bakeman, R.、Gottman, J. M.(1997)。Observing interaction: An introduction to sequential analysis。:Cambridge university press。
- Baron-Cohen, S.、Wheelwright, S.、Hill, J.、Raste, Y.、Plumb, I. (2001)。 The “Reading the Mind in the Eyes” Test revised version: a study with normal adults, and adults with Asperger syndrome or high-functioning autism。J Child Psychol Psychiatry, 42(2),頁 241-251。
- Brumbaugh, C. C.、Fraley, R. C. (2014)。 Too fast, too soon? An empirical investigation into rebound relationships。Journal of Social and Personal Relationships。 doi: 10.1177/0265407514525086
- Gottman, J. M.(2014)。What predicts divorce?: The relationship between marital processes and marital outcomes。:Psychology Press。
- Johnson, B.、Murray, K.(2008)。搞定怪咖情人(Crazy Love:Dealing With Your Partner’s Problem Personality)(柯乃瑜譯)。台灣:印刻。
- Jones, E. E.、Berglas, S. (1978)。 Control of attributions about the self through self-handicapping strategies: The appeal of alcohol and the role of underachievement。Personality and Social Psychology Bulletin, 4(2),頁 200-206。 doi: 10.1177/014616727800400205
- Le, B.、Dove, N. L.、Agnew, C. R.、Korn, M. S.、Mutso, A. A. (2010)。 Predicting nonmarital romantic relationship dissolution: A meta-analytic synthesis。Personal Relationships, 17(3),頁 377-390。 doi: 10.1111/j.1475-6811.2010.01285.x
- Mustonen, U.、Huurre, T.、Kiviruusu, O.、Haukkala, A.、Aro, H. (2011)。 Long-term impact of parental divorce on intimate relationship quality in adulthood and the mediating role of psychosocial resources。Journal of Family Psychology, 25(4),頁 615。
- Spielmann, S. S.、MacDonald, G.、Wilson, A. E. (2009)。 On the Rebound: Focusing on Someone New Helps Anxiously Attached Individuals Let Go of Ex-Partners。Personality and Social Psychology Bulletin, 35(10),頁 1382-1394。 doi: 10.1177/0146167209341580
- Wolfinger, N. H. (2007)。 Does the rebound effect exist? Time to remarriage and subsequent union stability。Journal of Divorce & Remarriage, 46(3-4),頁 9-20。
- 吳姵瑩(2017)。做自己最好的陪伴:找回安全感,讓你內在小孩不害怕、不寂寞的療癒五堂課。台北:遠流出版。
- 岡田尊司(2017a)。孤獨的冷漠:逃避型依戀障礙的分析與修復(邱香凝譯)。台灣:聯合文學。
- 岡田尊司(2017b)。戀愛這種病:解讀自我與對方的人格,診斷愛情的現在與未來(張婷婷譯)。台灣:時報出版。
- 胡展誥(2017)。別讓負面情緒綁架你:30個覺察+8項練習,迎向自在人生。台灣:寶瓶文化。