變身沙贊靠閃電夠力嗎？會是能源解方還是一場災難？《沙贊！ 》中的神力閃電之謎

從無法逆轉的抉擇，到平行時空

但人總喜愛想像，現實世界中無法「重頭來過」，但小說和電影的虛擬世界當然可以。在好萊塢電影《今天暫時停止》（Groundhog Day, 1993；港譯：《偷天情緣》）之中，男主角最先猶如惡夢般不斷在同一天的清晨醒來，後來卻利用這個機會不斷改善他的追求技倆（不但 take two，更take three、take four……），最後贏得美人歸。

電影為觀眾帶來了美滿的結局。但筆者最早領略「如果」作為小說創作中的奇思妙想，卻令我傷感不已。話說筆者自初中已經愛上科幻小說。大概是中三、四那年，我在公共圖書館借了一本英文的短篇科幻小說集，其中一個以「如果」為題的故事（名稱早已忘記）令我畢生難忘。

故事中，一對恩愛的小夫妻駕車外出，丈夫有點兒不適所以改由太太開車。不幸途中遇上車禍，坐在司機位的太太重傷身亡。丈夫悲痛不已終日借酒澆愁，揮之不去的自責是「如果我那天沒有跟她對調位置……」。

一天，他在拾理太太的遺物時，竟然發現她的日記簿中有新的記事！讀將下來，原來在另一時空裡，兩人當天的確沒有對調位置，所以因車禍去世的是他而不是愛妻！

這兩個「平行時空」原本不會重疊，卻不知怎的透過這本日記簿接通了。結果，「陰陽相隔」的倆人藉著日記互訴衷情。

這本已是十分淒美的情節，但後來日記中的字樣變得愈來愈模糊，最後完全消失，表示兩個「平行宇宙」最終分離而回到互不相通的狀態。筆者當年雖然只有十五、六歲，被觸動的哀愁卻是久久不能平復……。

年少的我已經深深感受到，人生中充滿了無數偶然的變數，而一個簡單的決定，足以改變一生。

多年後，我看到另一部電影《雙面情人》（Sliding Doors, 1998；港譯：《緣分兩面睇》），發覺也是用上了同一意念：女主角每天搭地鐵上班，但某天因事遲了一點而趕不上平日搭的那班車。電影基於「趕得及」和「趕不及」兩種情況，描述了女主角往後出現的兩種截然不同的人生。（我後來才知道，這乃改編自一部一九八一年的波蘭電影。）

歷年來，運用這類意念創作的小說和電影可謂不少，近年流行的好萊塢「超級英雄」電影中，《奇異博士》（Doctor Strange, 2016）和它的續集《奇異博士 2：失控多重宇宙 》（Doctor Strange in the Multiverse of Madness, 2022；港譯：《奇異博士 2：失控多元宇宙》）更將「平行時空」的意念延伸為「多重宇宙」（Multiverse）。陣容更為龐大的《復仇者聯盟 3：無限之戰》（Avengers 3: theInfinity War, 2018）和《復仇者聯盟 4：終局之戰》（Avengers 4: Endgame, 2019）皆以同樣的意念作為故事主軸。當然，這些電影都由漫畫改編，亦即這些意念的出現時間比電影還要早得多。

但將這個意念發揮至極的，毫無疑問是二○二三年橫掃奧斯卡最佳電影、最佳導演、最佳編劇多項大獎的「怪雞」¹ 電影《媽的多重宇宙》（Everything, Everywhere All At Once，縮寫是 EEAAO；港譯：《神奇女俠玩救宇宙》）。華裔演員楊紫瓊（1962-）更因此而封后（最佳女演員）；同樣是華裔的關繼威（1971-）以及潔美．李．寇蒂斯（Jamie Lee Curtis, 1958-）則分別獲得最佳男、女配角的殊榮。電影由兩位導演掌舵，雖然兩個都叫 Daniel，但一個是香港人關家永（Daniel M. Kwan, 1988-），一個是美國人丹尼爾．舒奈特（Daniel Scheinert, 1987-）。² 囊括了這麼多大獎，電影的風頭可謂一時無兩。由於有這麼多華人參與其間，全球絕大部分華人皆感到與有榮焉。

外國的評論幾乎一面倒地對這部電影讚譽有加，包括其中所包含的深刻人生哲理、愛情與理想之間的抉擇、亞裔移民在美國所遇到的生活困難、世代之間的價值矛盾、同性戀（非主流性取向）的社會認同問題，以及貫穿電影的、最重要的母、女之情。不少網友更留言說看至結局時感動流涕。反倒在華人世界，包括不少筆者所認識的朋友，皆對電影甚有保留，認為它寫情的部分毫無新意，而「科幻」的主題和情節則過於胡鬧不知云。（一些更認為電影被大肆吹捧，是近年席捲西方的「政治正確主義」的結果。他們更為另一位最佳女主角競逐者凱特．布蘭琪（Cate Blanchett, 1969-）不值。但那是另一篇文章的主題，暫且按下不表。）

註解

1. 粵語，意指奇怪、荒謬。
2. 因二人名字皆為「Daniel」，而被合稱為「Daniels」。

——本文摘自《超次元．聖戰．多重宇宙》，2023 年 11 月，二○四六出版，未經同意請勿轉載。

• 作者／劉柏宏
  • 勤益科技大學基礎通識教育中心教授

• Take Home Message
  • 電影《奧本海默》中，對於幾位匈牙利數學家如馮紐曼、波利亞等人的描述篇幅較少，但他們其實對科學界影響深遠。
  • 馮紐曼在曼哈頓計畫中建議以內爆透鏡設計原子彈，不僅所需的裂變材料較少，又可以防止原子彈過早引爆，達成更對稱與高效的爆炸。
  • 波利亞提出以「捷思法」等強調歸納實驗的方式思考數學問題，例如觀察找出數學公式的形成，此法也掀起了數學教育革命。

遊艇緩緩流動在分隔布達區（Buda）與佩斯區（Pest）的多瑙河上，絲絨般的水波、柔棉沁涼的河風，兼容哥德式與文藝復興建築風格的匈牙利國會大廈（Hungarian Parliament Building）圓頂，在夕陽的烘托之下宛如紅寶石般璀璨，流瀉出昔日奧匈帝國的風華。

筆者來到此地，終於可以想像為何 100 年前這條河的兩岸能夠孕育出一批改變科學面貌，甚至改變人類歷史的數學家與科學家。趁著今（2023）年暑假到布達佩斯開會之便，筆者也試著踏尋這些科學家的足跡。

回臺灣之後恰逢電影《奧本海默》（Oppenheimer）上映，儘管許多人聚焦在主角奧本海默（Julius Oppenheimer）的內心世界，不過筆者更關心的是幾位被火星人遺留在地球上的匈牙利數學家。

地球上的火星遺民

20 世紀初歐美科學圈流傳著一個神祕的傳說，記錄下這傳說的是匈牙利物理學家馬克思（György Marx），但傳說起源卻得從義大利物理學家費米（Enrico Fermi）說起。

1950 年某個夏日午後，費米在美國原子彈曼哈頓計畫（Manhattan Project）的基地——洛斯阿拉莫斯國家實驗室（Los Alamos National Laboratory），和幾位科學家聊到當時有關幽浮的報導時，提出了一個問題：

「宇宙如此浩瀚，包含無數恆星，許多恆星和太陽沒什麼差別，也有行星圍繞著它們旋轉。一部分的行星地表也會有水和空氣，而來自恆星的能量將促使有機化合物合成。

這些化學物質將相互結合產生一個自我複製系統。最簡單的生物會通過自然選擇繁殖、進化並變得更加複雜，直到最終出現活躍的、會思考的生物，文明、科學和科技隨之而來。

由於對美麗新世界的渴求，他們會旅行到附近行星，然後到另一個恆星的行星。他們最終應該遍布整個銀河系。這些非凡和傑出的人很難忽視像地球這樣美麗的地方。

所以，如果真是如此，他們必定來過這裡。那麼，他們到底在哪裡？」

關於這個「費米問題」，匈牙利物理學家西拉德（Leo Szilard）的回應是：「他們就在我們身邊啊！只是他們自稱匈牙利人！」（They are among us, but they call themselves Hungarians.）。

西拉德的高級幽默，點燃匈牙利人是火星遺民的想像，各種附和的說法紛紛出籠。有一種說法是 19 世紀末至 20 世紀初，一艘來自火星的太空船降落在地球，由於發現匈牙利的女子美麗又性感因而定居下來，繼而繁衍後代。

後來太空船要返回火星時超重，不得不將一些人留下，這些人包括建議當時美國總統羅斯福（Franklin Roosevelt）發展原子彈的信函主要起草人西拉德、協助潤稿的泰勒（Edward Teller）和諾貝爾物理學獎得主維格納（Eugene Wigner），還有化學獎得主歐拉（George Olah）與波拉尼（John Polanyi）、經濟獎得主哈薩尼（John Harsanyi）；以及數學家艾迪胥（Paul Erds）、波利亞（George Pólya）、馮紐曼（John von Neumann）、哈爾默斯（Paul Halmos）、拉克斯（Peter Lax）等人。

這幾位科學界的火星遺民有許多共同點：他們都出生於匈牙利。

除了喜歡雲遊四海的艾迪胥外，他們後來都移居並任教於美國的大學；他們思考問題時都喜歡來回踱步；另有一個最不可思議的共同點——他們都是猶太人。

至於為何火星人特別鍾情猶太人？這可能又是另一個「費米問題」。

《奧本海默》的最大遺珠——馮紐曼

筆者本次開會的地點在羅蘭大學（Eötvös Loránd University），該校在過去不同時期曾名為布達佩斯大學（University of Budapest）、帕茲馬尼－彼得大學（Pázmány Péter Catholic University）。

該校培育出不少數學家與科學家，而馮紐曼是箇中翹楚。

馮紐曼出身於布達佩斯的富裕猶太家庭，父親是位對他有很深期待的銀行家，希望兒子能往化學工程發展，但馮紐曼卻對數學情有獨鍾。有許多關於他的數學傳奇事蹟，例如 6 歲能心算八位數除法，8 歲熟悉微積分，15 歲開始學高等微積分，19 歲已經發表兩篇數學論文。

最後馮紐曼不違父願也無逆己志，不僅在蘇黎世理工學院（Eidgenössische Technische Hochschule Zürich, ETH）讀化工，同時也在帕茲馬尼－彼得大學研修數學博士。

有鑑於在 19 世紀末和 20 世紀初，德國數學家康托爾（Georg Cantor）的集合論導致某些推論會產生矛盾難題，即使在當時產生的矛盾並非集合論的核心，但在嚴格檢驗非核心的部分時，邏輯上還是會發現一些瑕疵，因此馮紐曼選定了與集合論基礎有關的內容深入研究。

他的博士論題目為〈一般集合論的公理化構造〉（Az általános halmazelmélet axiomatikus felépítése），並於 1926 年同時取得兩所大學的博士學位。

而後在洛克菲勒基金會（Rockefeller Foundation）的資助下，他前往德國哥廷根大學（University of Göttingen），師從德國數學家希爾伯特（David Hilbert）。

1933 年為逃避納粹對猶太人的迫害，馮紐曼應聘前往美國普林斯頓高等研究院（Institute for Advanced Study），在那裡開始專研計算機科學，同時也結識了奧本海默。

建議原子彈採用「內爆式」設計的馮紐曼

由於馮紐曼的博學與優異數學計算能力，奧本海默聘請他作為曼哈頓計畫的顧問，主要負責兩項任務：一是研究內爆透鏡的概念和設計，二是負責預估炸彈爆炸的規模、死亡人數，以及炸彈爆炸的離地距離以達到最大效果。

什麼是內爆透鏡？當時曼哈頓計畫考慮的核分裂方式有兩種，一種是「槍式核分裂」（gun-type fission）設計，另一種則是「內爆透鏡」（implosion lens）的設計。

槍式核分裂設計是仿造子彈的射擊方式，利用常規炸藥將一塊次臨界物質射向另一塊可裂變物質，使可裂變物質達到臨界質量（圖一）。

槍式核分裂使用鈾（uranium, U）作為裂變材料，二戰時投擲於日本廣島的「小男孩」（Little Boy）就是採用槍式設計。但由於當時鈾的存量並不足夠，因此必須發展另一種形式的原子彈，也就是內爆透鏡設計。

內爆透鏡設計以鈽（plutonium, Pu）作為裂變材料，在空心的球狀空間內放置鈽，並在球形鈽彈周圍放置炸藥。這些炸藥爆炸同時產生的強大內推壓力將會擠壓球形鈽彈，引發連鎖反應造成核爆（圖二）。

馮紐曼評估之後，認為「內爆式」設計優於「槍式」設計，且內爆型原子彈所需的裂變材料較少，又可以防止過早引爆以達成更為對稱與高效的爆炸，因此建議奧本海默改發展內爆式核彈，這就是二戰時被投放到日本長崎的原子彈——「胖子」（Fat Man）。馮紐曼在曼哈頓計畫中的角色如此關鍵卻被電影所忽略，確實令許多人不平。

馮紐曼從小嶄露他的優異天賦且記憶力驚人，除數學領域之外在諸多科學分支也有所涉獵且精通。他的聰慧早已獲得同儕的認同與讚譽，常被稱為數學界最後一位通才。有一個流傳甚廣的傳說是某次宴會中女主人問馮紐曼一個問題：

「兩列相距 200 英里的火車正在相向行駛，每輛火車的行駛速度均為每小時 50 英里。一隻蒼蠅從其中一列火車的前面出發，以每小時 75 英里的速度在火車之間來回飛行，直到火車相撞並將蒼蠅壓死為止。蒼蠅在這段期間總共飛行了多少距離？」

一般人解這一題可能是先算第一段時間蒼蠅飛行的距離，再算第二段時間蒼蠅飛行的距離，由於蒼蠅來回飛行無限多次，距離愈來愈短，可以用無窮等比級數求和的方法得出解，但這樣的計算相當繁複。有一個更快捷的技巧是直接算出兩輛火車將於兩小時後相撞，因此得知蒼蠅總共飛行 150 英里。

馮紐曼聽完問題不一會兒就答出 150 英里，女主人對於馮紐曼沒有陷入計算無窮等比級數的陷阱感到失望，但馮紐曼竟回答：「我是用求和的啊！」若此傳說當真，顯見他驚人的計算能力。

1963 年諾貝爾物理學獎得主維格納表示，他認識當代許多頂尖科學家，包含德國理論物理學家普朗克（Max Planck）、英國理論物理學家狄拉克（Paul Dirac）、西拉德、泰勒、愛因斯坦，但沒有一個人像馮紐曼般才思敏捷。曾有人問維格納為什麼匈牙利出現這麼多天才，維格納的回答是：「真正的天才只有馮紐曼一人。」

引發數學教育革命的波利亞

本文要介紹的第二位匈牙利數學家是波利亞。1912 年，他於布達佩斯大學取得數學博士學位後，便前往德國哥廷根大學從事博士後研究。他在哥廷根大學結識許多當代最傑出的數學家，例如希爾伯特和克萊因（Felix Klein），之後便到蘇黎世理工學院任教。相較於一般嚴謹木訥的數學家，波利亞相當擅長說故事，包含數學家的軼事和「說數學」的功力。

馮紐曼在蘇黎世理工學院修讀博士時，也曾上過波利亞的書報討論課。有次波利亞提到一個尚未解決的數學問題，他認為要證明這問題很困難，沒想到五分鐘之後馮紐曼舉手，然後在黑板上寫下證明，從此之後馮紐曼變成他最敬畏的學生。

另外，波利亞也曾談論有關希爾伯特的故事。在德國盛傳一個傳說，深受德國人敬愛的皇帝腓特烈一世（Friedrich I）沒有死亡、只是沉睡，等到德國需要他時他就會挺身而出。因此便有人問希爾伯特：「你若在死後 500 年復活，你會做什麼事？」希爾伯特說：「我會問是否有人證明了黎曼猜想（Riemann hypothesis）？」

黎曼猜想與質數分布具有密切的關係，是希爾伯特於 1900 年提出的 23 個最重要數學問題之一。有些數學家將證明黎曼猜想形容為「數學界的聖杯」，因此它的重要性可見一斑。2018 年 9 月 24 日，英國數學家阿蒂亞（Michael Francis Atiyah）宣稱他證明了黎曼猜想，此事件也曾轟動一時。

但阿蒂亞的證明還來不及得到同儕認證，便不幸於 2019 年 1 月 11 離世，截至目前為止數學界仍對阿蒂亞的證明有所質疑。所以如果希爾伯特現在真的死而復活，那他恐怕要失望了。

波利亞於 1945 年出版《怎樣解題》（How To Solve It）一書，展現他「說數學」的功力。他常強調數學有兩面，數學結果的呈現方式有如歐幾里得（Euclid）幾何學般的演繹論證形式，但數學知識發展過程卻更像是一門實驗歸納的科學。書中提倡以捷思法（heuristic）思考數學問題，例如高中時老師通常教學生如何證明 13＋23＋33＋43＋⋯＋n3＝，但卻很少說明究竟如何得到此公式。

波利亞則要學生先做探索觀察。例如從圖三可以發現前五個自然數的立方恰好都等於另一個自然數的平方，這樣的特殊性可以推廣為「前 n 個自然數的立方和等於某個自然數的平方嗎？」若可以推廣，某個自然數到底是哪個數？我們進一步觀察可以得到：1＝1, 3＝1＋2, 6＝1＋2＋3, 10＝1＋2＋3＋4, 15＝1＋2＋3＋4＋5，將這觀察和圖三結合就得到圖四中令人驚訝的結果。

這麼美麗的結果應該不會只是巧合，所以一個合理的臆測也因此誕生：「前n個自然數的立方和等於前n個自然數和的平方」，也就是 1³＋2³＋3³＋4³＋⋯＋n³＝（1＋2＋3＋4＋⋯＋n）²。由於 1＋2＋3＋4＋⋯＋n＝，所以得到 1³＋2³＋3³＋4³＋⋯＋n³＝這個「合理的」公式，接著就可以證明此結果的正確性。

由此我們看到捷思法可以展現一個數學公式形成的過程，如同在《奧本海默》電影中丹麥物理學家波耳（Niels Bohr）建議奧本海默改到哥廷根大學跟從玻恩（Max Born）學習理論物理。

波耳問奧本海默數學程度如何，並提醒他：「代數就像一本樂譜，重點不是你能否讀懂音樂，而是能否聽懂音樂。」（Algebra is like a sheet music. The important thing isn’t if you can read music; it’s if you can hear it.），波利亞的捷思法就是教我們如何聽懂音樂而不光是讀懂音樂。

在 1960 年代，美國由於憂慮太空競賽落後蘇聯，因而發起所謂「新數學」的中學數學課程改革，強調數學的抽象性，試圖讓學生早一點熟悉數學邏輯的演繹過程，但這種罔顧知識發展脈絡的改革註定以失敗告終。

1980 年代，波利亞強調歸納實驗思考過程的捷思法逐漸受到重視，掀起一波「數學問題解決」（mathematical problem-solving）的浪潮，而這股浪潮的影響也猶如核分裂的連鎖反應，持續至今。

• 〈本文選自《科學月刊》2023 年 11 月號〉
• 科學月刊／在一個資訊不值錢的時代中，試圖緊握那知識餘溫外，也不忘科學事實和自由價值至上的科普雜誌。

身為一名訓練師，你真的了解你的寶貝們嗎？寶可夢圖鑑讀熟了沒？

其實圖鑑告訴你的比想像中的還多喔！跟著泛科空想寫手 Rock 一起來上一門訓練師的科學課吧！來跟大家分析這些寶可夢的戰鬥是多麼的「科學」。

骨紋巨聲鱷：火焰溫度新紀錄

啊~火焰！

幻想世界中骨灰級的攻擊武器，也是空想科學寫作時常遇到的對手。

在過去的【科學寶可夢】中，火焰已經不是第一次出現了。第二篇關於噴火龍的科學中就有稍微提到，後來因為鴨嘴火龍和火伊布的圖鑑敘述都有提到他們火焰的溫度，所以在同一篇一起分析過，但那已經是第一世代寶可夢的事了~ 現在圖鑑都來到 900 號了，事情果然很不一樣。

「溫柔的歌聲能治癒聽者的靈魂，會使用攝氏 3000 度的火焰把敵人燒成灰燼。」——骨紋巨聲鱷紫版敘述^註1

骨紋巨聲鱷的敘述很直接，就是直接說出了牠噴出的火焰溫度，這簡直是一個福音，這樣我們就不需要到處拼湊，可以直接地將這個數字與過去的幾個得到的火焰溫度做比較。

噴火龍：至少 1400 ℃

鴨嘴火龍：1200 ℃

火伊布：1650 ℃

火爆獸：800℃

骨紋巨聲鱷：3000℃

這也太高了吧！？先別說生物怎麼有辦法產生這種高溫^註2，真的要把人燒成灰燼哪裡需要 3000℃ 啦！

一般把屍體燒成骨灰的火葬場，溫度只需要 1000℃ 就夠了，3000℃ 根本是大材小用，而你知道這個溫度能夠辦到什麼事嗎？

絕大部分我們知道的物質在這種溫度下都會熔化或者汽化，能夠倖存的元素大概只有鎢、錸、鋨這幾個金屬還有一些特殊的聚合物了；如果燒的是人的話，別說是燒成灰，整個身體一定在一陣白光下消失的無影無蹤……因為在這種溫度下，火焰不會是正常的橘紅色，而是白色的。

這時如果骨紋巨聲鱷的訓練師就直接站在它旁邊，就算不是被直接擊中，他那超過岩漿溫度兩倍的 3000℃ 火焰所散發出的熱氣和輻射熱^註3，應該足以讓訓練師瞬間嚴重灼傷，再加上強光，這絕對是不支倒地然後變成逐漸變成焦屍，然後跟四周的花草樹木付之一炬。

所以如果要叫你的骨紋巨聲鱷使出噴射火焰的話，記得先閃的非常非常遠，放招後遠距離收回寶可夢，然後趕快離開被焚化、整個燒得亂七八糟的現場。

狂歡浪舞鴨：這到底是哪一國的超強踢腿舞啊？

如果要說格鬥系的寶可夢要怎麼在圖鑑中誇耀他們的力量，最常用的方式就是：把東西丟出去或弄壞。

在以前的的腕力+豪力+怪力的文章中，我們可以看到各種誇耀寶可夢力氣的方式，例如、「能夠跟 100 個成年人角力把他們摔出去」、「可以用一隻指頭舉起相撲選手」、「有辦法舉起一台垃圾車」、「把人打飛到地平線彼端」……等。

而這次，我們的狂歡浪舞鴨的特技是能夠踢翻一台卡車。

「只要一腳就能踢翻卡車的強韌腳力，展現充滿異國風情的舞蹈。」——狂歡浪舞鴨朱版敘述^註4

要計算這有多誇張，我們需要知道一個非常重要的資訊……究竟是哪一種卡車呢？

卡車這種交通工具有非常非常多的規格，最輕的例如小皮卡只有 2~2.5 公噸，最重的可以達到 15 公噸，甚至在某些重工業地區可以找到更重的運貨卡車。

寶可夢朱／紫據稱是參考西班牙為藍本設計的，經過一番搜尋之後，筆者得知西班牙地區是全歐洲輕型卡車比例最高的地方^註5，這類卡車本身重大概介於 3~4 公噸之間，如果滿載貨物的話，重量可以達到 10 公噸以上，我們這邊就大概取個平均值 7 公噸好了。

然後我們還得先定義踢翻卡車這件事情：我們就假設狂歡浪舞鴨用腳朝卡車的側面一半高的地方踢下去，然後車子會以一邊的車輪為支點翻過去，側面著地。

經過一些力矩的計算，我們可以知道要把一台 7 公噸重的卡車踢翻，需要從從中間給予大約 68600 牛頓的力……這可比一台小汽車引擎全力輸出時的力道還要強啊~

但是最誇張的還在後面！

最後一步，我們想要知道狂歡浪舞鴨的這一腿到底有多快！要得到這個結果，筆者需要知道此鴨的整隻腳重量為何，因為畢竟是腳在對卡車施力的。

圖鑑上寫說狂歡浪舞鴨體重為 62 公斤，而牠的外貌滿接近人形生物的，所以我們先參考人體結構來預估。人類的一整支腳平均占全身體重的 16~18% 左右，我們的狂歡浪舞鴨看起來腿略長，而且既然是格鬥系的，那牠的腿應該很壯，我們就假設牠的整隻腿重量占比更多，大概是全身的 25%，重量的話就是差不多 15.5 公斤。

要計算牠這腿速度多少，我們最後剩下需要的假設的就是假設腿和卡車的接觸時間，依照之前的經驗，就姑且設定為 0.1 秒接觸，然後腿踢中之後立刻停下，再加上很不合理的力道 100% 轉換假設，但是相信我~不這麼做的話答案只會更扯。

套入牛頓第二運動定律的公式，我們可以知道這腿在停下來之前，速度高達秒速 443 公尺，也就是音速的 1.3 倍，這也太快了吧！你的腳怎麼沒有被音爆撕裂啊？相較之下，泰拳高手秒速 17 公尺的踢擊根本是個笑話，如果被狂歡浪舞鴨的這一腳踢到，我看大部分的寶可夢應該是內臟破裂死亡了。

這真是太恐怖了，但狂歡浪舞鴨你為什麼無聊要去踢卡車啊？這種腳力你應該要去踢足球啊！還有這到底是哪一國的舞蹈會有如此的訓練呢？真想知道~

註解:

1. 骨紋巨聲鱷的另一版敘述是「可以透過歌聲改變外形的火鳥，據說是靈魂寄宿在頭上的火球所形成的。」，從這個敘述我們知道牠的火焰跟某種靈魂力量有關，這大概就是為什麼火焰溫度能達到 3000 度的秘訣吧？話說筆者很確定是這裡的溫度是說攝氏，因為英文版的敘述中有寫是 5400 華氏。
2. 也有可能……骨紋巨聲鱷根本不是生物！畢竟牠有幽靈屬性，但這表示牠的出現根本不是進化，而是死亡呢？
3. 這裡我們因為 3000℃ 的火焰而傷透腦筋，但你知道嗎？這還不是寶可夢圖鑑裡最扯的，有兩隻寶可夢：熔岩蝸牛 和 噴火駝，他們的圖鑑敘述都寫到牠們能夠產生 1 萬度 ℃ 的高溫，前者是體溫，後者是噴出的岩漿，這確定不是多寫一個0嗎? 目前科學家有辦法產出最高的溫度只有 4990℃ 而已啊~
4. 狂歡浪舞鴨另一版的敘述是「會用充滿異國情調的舞蹈迷倒看到的對手，然後揮舞以水構成的羽飾將其劈裂。」為什麼羽飾是用水構成的啊？這是怎麼辦到的？這跟強力水刀差在哪裡？
5. 幸好這代寶可夢不是參考德國，因為這是歐洲重型卡車比例最高的地方，如果狂歡浪舞鴨源自這裡，他這一腳一定超出天際。

「沙贊！」然後一道閃電就會打下來，擊中一位青少年，瞬間變成一位穿著紅衣+披風、渾身肌肉的（中二）成年人，這就是 DC 宇宙中，超級英雄沙贊的變身過程。

很有趣的是，大家可以回想一下，最近這 10 幾年來席捲世界的漫威和 DC 英雄，絕大部分執行英雄行動前都是進行「著裝」，例如鋼鐵人、蝙蝠俠、美國隊長……等，但是沙贊不一樣，儘管不複雜，但他需要一套特別的手續來改變他自己的身體，已獲得他身為超級英雄的力量，這點跟日本的超人力霸王比較類似。

根據 DC 宇宙的設定，賦予沙贊力量、讓他變身的閃電都來自神界的奧林帕斯山，只要他大喊一聲，閃電就會隨傳隨到，而因為一切是神力的關係，理論上他接收力量的位置無關緊要，也非常的安全。

真不愧是奧林帕斯山啊！如果我們能夠在比利（電影中變身成沙贊的少年）的頭上裝一個收集閃電能量的器材，那費城一定變成全美國能源最豐沛的城市。

但是要進行超級英雄活動，普通的閃電能量夠嗎？這道奧林帕斯山的閃電會不會是一道超越人類認知的超級閃電呢？

還有儘管沙贊不會受影響，但如果有人不小心在變身時不小心碰觸他或在他附近，會發生什麼事呢？

這真的值得一起來探討～

先定立標準：閃電能提供多少能量？

閃電是大自然中最純粹的能量展現之一，經過大氣學家的觀測和預估，一道閃電電壓大概是 3 億伏特，帶有 10 億焦耳的能量，這差不多是燃燒 30 公升左右的汽油。

聽起來非常的厲害，那我們利用閃電來獲得能源會不會是個好方法？

其實從 1980 年代開始科學家就有這種想法，但是他們發現這其實很不切實際，主要原因有幾個：閃電很難預測、傳導到地面上能量又會大減、效率很不穩定……但那是大自然的閃電，讓沙贊變身的可是充滿神力的閃電耶！不只能夠提供沙贊穩定且高能的能量來源，還可以藉由跟蹤比利知道閃電的位置和時間。

我們只要把比利抓起來請出來，跟他預約時間大喊沙贊，就可以發電了～

現在的問題是……這道閃電有多少能量呢？

要知道一道神奇閃電帶有多少能量其實有點困難，因為一旦比利變身之後，他似乎沒有時間限制，不像超人力霸人那樣有 3 分鐘的活動上限，後者會比較好估算是因為你可以設想這 3 分鐘內超人力霸王做了哪些事情，在逐一拆解。

所以筆者覺得最能夠執行的方式，是羅列出電影中沙贊一次變身基本上會做到的事情，這樣結果應該就足夠是神力閃電的基本盤。

從電影《沙贊！眾神之怒》中，筆者列出幾個沙贊在超級英雄狀態時做的事，包括:

1. 以音速飛行 10 分鐘
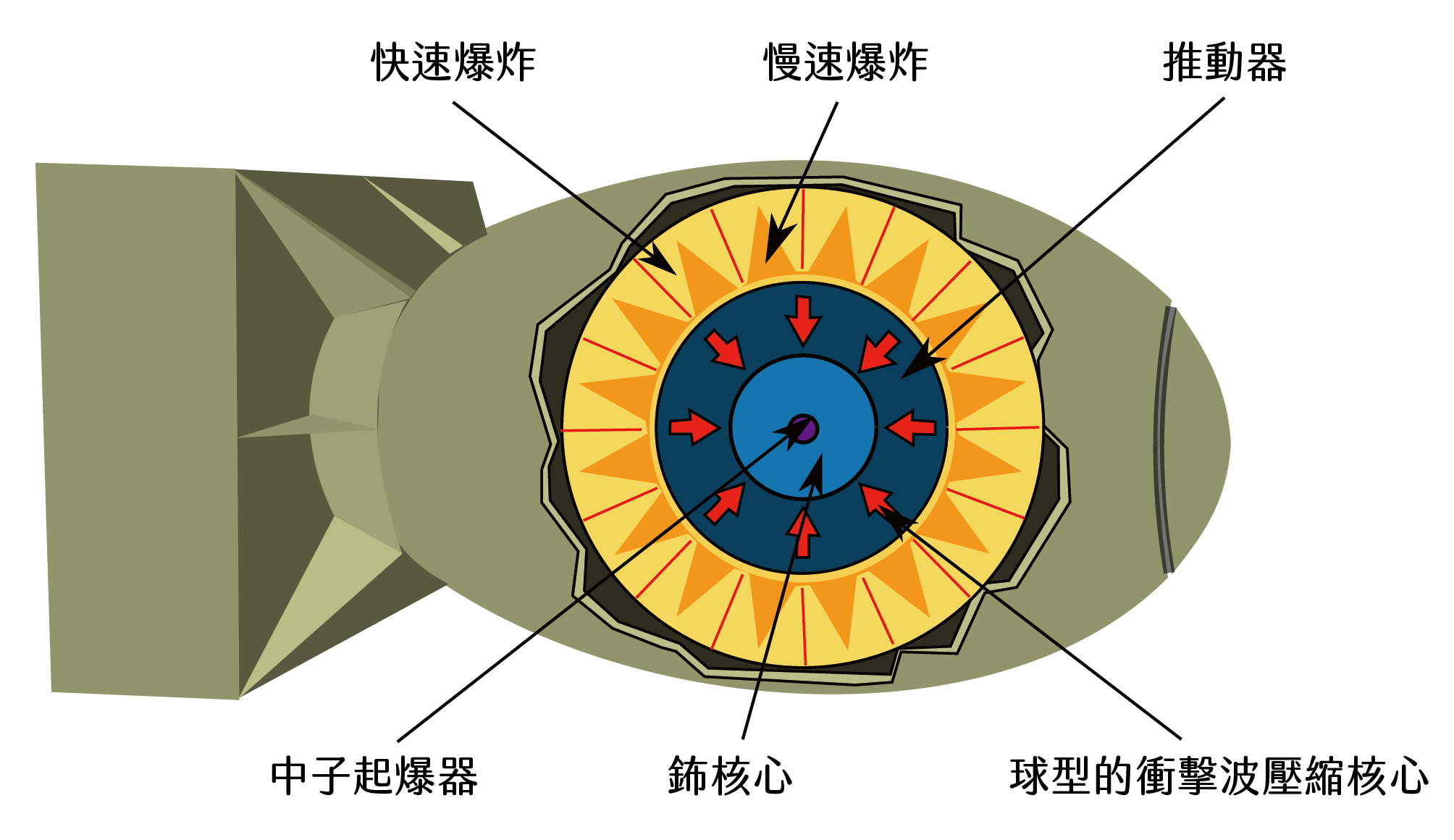
2. 把一隻體型巨大的飛龍打飛 10 公尺
3. 把一台車移動 200 公尺
4. 從手中放出好幾道像特斯拉線圈的能量閃電

這樣感覺差不多了吧……等等～還有一件很重要的事，就是這道閃電同時還把一名 17 歲的青年變成一名看起來 30 歲的成年人，這瞬間成長所需的誇張能量應該也要算進閃電的功勞裡，所以這個列表還要加進另一項:

5. 讓 17 歲的青年成長成 30 歲男性的所需熱量

那我們接下來可以逐一估算了。

• 那首先就來計算成長所需的熱量吧！

要讓人成長的能量，其實也是熱量，也就是大家耳熟能詳的卡洛里，1 千大卡的熱量差不多是 4184 焦耳的能量。

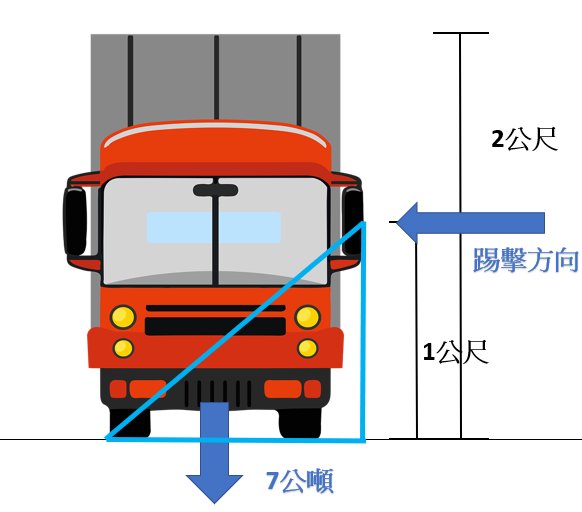
根據衛服部提供的資料，一名成年人每日所需的熱量依他的活動量和體重來決定，那沙贊毫無疑問絕對是重度活動量那一類的，體重的話少年比利看起來介於 60~70 公斤之間，而飾演沙贊的演員柴克萊威曾說為了演戲需要增重到超過 90 公斤，雖然隨著體重增加每日所需熱量也會不同，但為了簡單估算，我們姑且用 80 公斤算到底吧～

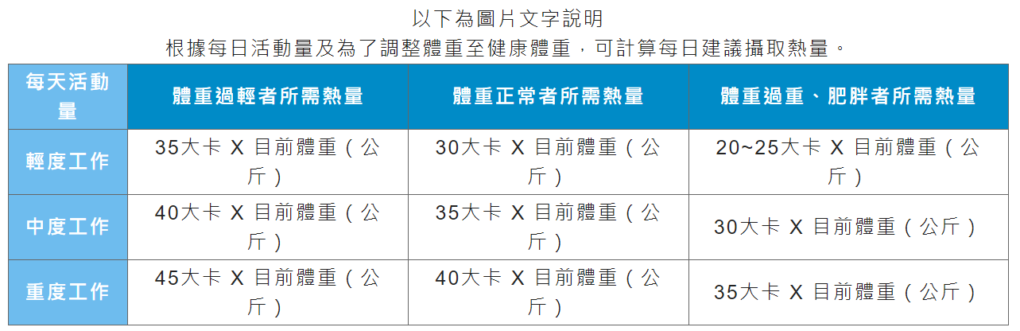
比利瞬間成長為超人般壯碩所需能量= 40 大卡 x 80 公斤 x 365 天 x (30-17) 年 x 4184 J= 6.35x 10¹⁰ 焦耳 = 635 億焦耳

這數字怎麼已經有點大了……但在吐槽之前，我們先把其他的所需能量都估算完吧～

• 以音速飛行 10 分鐘

這裡我們借用四分之一英里估算法，這是個可以從物體重量（通常是車子）和行駛四分之一英里所需的時間來求得功率的簡單方式。

沙贊體重 90 公斤，而他在音速下完成 1/4 英里所需的時間為 1.2 秒，根據線上工具估算，這名英雄相當於擁有 22,876 馬力，轉化為瓦特差不多是 1700 萬瓦特，如果沙贊要飛行 10 分鐘，他就會需要大約 100 億焦耳的能量 。

• 把一隻體型巨大的飛龍打飛 50 公尺

這個計算方式並不困難，就是簡單的做功運算，但是筆者遇到了很嚴重的問題：電影中的飛龍-拉頓到底多重呢？

經過一番搜尋，網路上對於一條中世紀奇幻飛龍到底有多重幾乎是沒有定論，看起來好像沒有人有認真算過，所以筆者打算自己來操刀，解決這個世紀大謎題 (?)。

有看過《空想科學讀本》的人對筆者使用的方法一定不陌生，就是把模型浸到水裡面，估算體積之後放大，再考慮密度來求得飛龍的體重。

所以筆者到了地下街的玩具店，買了一條看起來最像電影中奇幻飛龍體型的模型玩具（其實是動漫《轉生成為史萊姆》的公仔，似乎是主角後期的樣子吧？筆者沒有看不清楚~），將它放進水盆裡面裝水，做好水位標記之後取出模型，水位下降之後從水盆的面積和下降高度求得玩具龍的體積大概是 0.000283 立方公尺，這時我們需要玩具龍的身長和電影中的拉頓身長來做等比放大，玩具龍身體差不多是 25 公分，而從電影中拉頓站在棒球場內野的畫面來做估算，它的身長大約是 25 公尺，身長差 100 倍，所以體積會變 100 的 3 次方也就是 100 萬倍，所以說拉頓的體積大概是 283 立方公尺。

這時我們需要拉頓身體的密度來求得體重，如果拉頓是生物的話，它的身體密度應該也要接近水（每立方公尺 1000 公斤），例如人體的密度就差不多是每立方公尺 1062 公斤，但是電影中拉頓身體看起來有點像是由木頭構成的，而世界上最堅硬的木頭是澳洲鐵木樹（Australian buloke）密度是 1085 kg/m3，再加上龍的奇幻性質，我想把拉頓的身體密度定為 1100 kg/m3 應該是還可以接受的吧？

如果用這個方式估算，電影中看守花園的飛龍拉頓，體重大概會是 311 公噸，我們套入物理課本中看過的做功計算公式，可以知道沙贊把一條龍打飛 50 公尺所需要的能量，大概會是 7775 萬焦耳。

• 把一台車移動 200 公尺

相較前面兩個，這計算相對簡單一點，我們一樣用上面的作功公式來求需要能量，而我們需要的就是車子的重量。根據統計，美國一般路上的車子平均重量為 1800 公斤，如果要在 3 秒鐘內移動 200 公尺，就相當於需要 4 百萬焦耳。

• 從手中放出好幾道能量閃電

沙贊從手上放出閃電，看起來就像是電弧的一種，而電弧是因為有強大的電場或高壓電存在，使的原本不導電的物質電漿化得以使電流通過的現象，而說到能夠最穩定產生電弧的狀況，筆者第一個想到的是在現實中會看到的特斯拉線圈。

特斯拉線圈是一種由知名物理學家特斯拉發明的強大變壓器，這種變壓器使用共振原理運作，主要用來生產超高電壓但低電流、高頻率的交流電力，因為特斯拉線圈可產生絢麗的電弧效果，所以很常在一些科學博物館或展示中看到，而世界上最強大的特斯拉線圈： Electrum 的能量使用率為 130,000 瓦特，假設沙贊能夠用同等功率放出電弧長達 10 秒鐘，就會需要 130 萬焦耳的能量。

這下子我們需要的數字都有了！

這道神奇閃電所附帶的能量大約是：

635 億（變成大人）+100 億（音速飛行 10 分鐘）+7775 萬（打飛一條龍）+400 萬（移動一台車）+130 萬（放出閃電）= 735 億 8305 萬焦耳

 而正常世界一道閃電的能量大約是 10 億焦耳，也就是說～這道神奇閃電差不多是等於 74 道現實中閃電的能量。

好厲害啊！真不愧是奧林帕斯的眾神，能夠這麼精準的傳遞如此巨大的電能量根本就是神蹟…..也確實是神蹟沒錯～

但是如果一個不小心承接這道能量的人不是沙贊的話，會發生什麼事呢？

一般人被普通的閃電擊中就已經不是鬧著玩的了！

直接被閃電擊中的人會成為電流的一部分，一部分電流會沿著皮膚表面移動，另一部分會穿過身體的心血管或神經系統，前者會對皮膚造成灼傷，後者則有可能造成呼吸停止或心臟驟停，但我們還是能找到一些歷史上從雷擊中生還的故事，因為有沒有辦法在雷擊中活下來是跟就醫和電流通過體內的時間而定……運氣好的話，你不會死的。

但是在沙贊的神奇閃電面前，這一切都成為笑話。

這道 735 億焦耳的閃電能量相當於 2 顆歷史上最強大非核子炸彈：炸彈之母（GBU-43/B 大型空爆炸彈）爆炸所釋放出的能量，所以如果今天好死不死沒有打在比利身上，而是擊中地面的話，後果一定不堪設想，周遭的親友絕對是灰飛煙滅，費城可能會變成廢墟，之前說的收集能量可能完全行不通，因為應該沒多少設備儀器能夠承受如此巨大的威力。

反倒是比利啊~你是不是在承接沙贊能力時同時被改造了，被2顆炸彈之母轟炸都沒事，真是太神啦！還有就是一定要站好喔～