- 文/林祉均
從《瑞克與莫蒂》到最近的《媽的多重宇宙》和《奇異博士2:失控多重宇宙》,多重宇宙的浪漫概念一直是各種作品愛用的元素。主角穿越到其它平行宇宙中,遇見各種不同的可能性,實現未能完成的心願。
可惜的是,現實中似乎沒有這種好事情。眼睛所看到的世界就只有一個,一切就照著原本的劇本發生,沒有穿越或是重來的機會。
不過,這些幻想作品的描述,其實並不如你所想的這麼天馬行空。創作科幻作品所需要的想像力,對於科學家來說,其實也是重要的技能。打從二十世紀中期開始,正經的量子物理討論中,便出現了「多重世界」的說法。
「多重世界」是對於量子現象許多詮釋中的其中一種。實事求是的物理學家為什麼要訴諸這麼虛幻的說法呢?說到底,他們也是情非得已。這一切要從量子物理帶給他們的難題說起。
在量子時代前,物理學家的世界
在量子時代之前,物理學家用來解釋世間萬物的方法是「古典力學」與「電磁學」。
- 「古典力學」是「牛頓運動定律」的進階版,解釋了「具有質量的粒子(物質)如何運動」
- 「電磁學」則是一切電磁波相關技術(你的手機訊號)的基礎,解釋了「不具質量的能量如何在空間中以波動傳遞」。
「古典力學」與「電磁學」把世間分成「粒子」與「波動」兩種不同的問題來解釋,彼此井水不犯洪水,分別「近乎完美地」解釋所有日常生活中常見的現象,然而,有一個現象在深入研究之後,卻出現了矛盾,這個現象就是雙狹縫實驗(Double-slit experiment)。
雙狹縫實驗的詭異之處
如果讓光束通過一條狹縫,會在後方的屏幕映照出中間較亮,兩側較暗的圖樣。奇妙的是,如果將實驗改成兩條狹縫,屏幕上的圖案並不會等於兩個單狹縫的圖案相加,而是會變成亮暗間隔的條紋。這種圖案只能由波動產生,因為波峰和波谷會互相抵銷,因此產生較暗的部分。
雙狹縫實驗成為了光是波動的證據,屬於「電磁學」解釋的範疇,後續的推導也證明了光是一種電磁波。

如果故事停在這裡倒也還好,但後來卻觀測到「用電子或中子打入雙狹縫,也會得到跟光進入雙狹縫時類似的結果」。
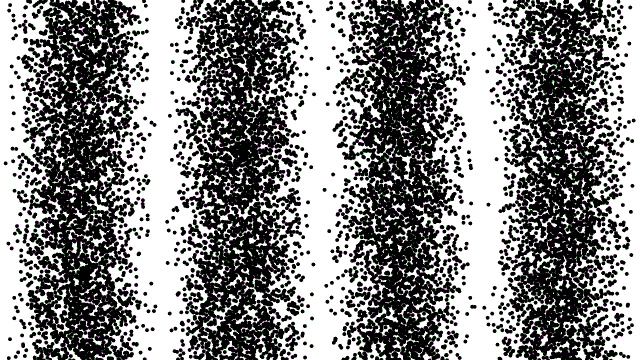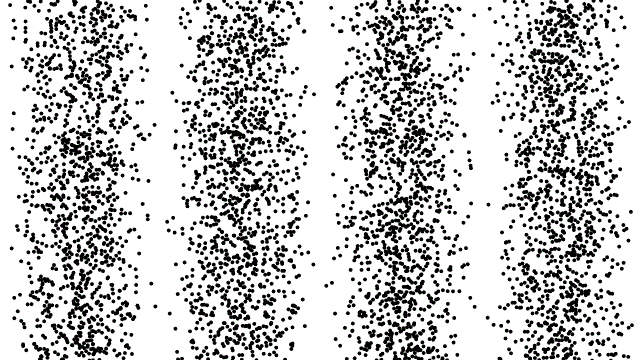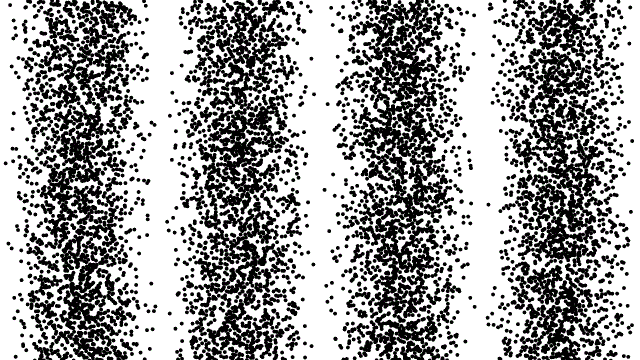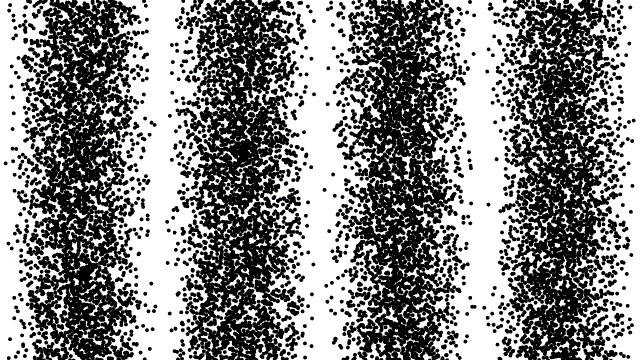
這問題就有點大了,因為電子或中子這些粒子的運動,在雙狹縫實驗時必須要跟光一樣,用波動才能解釋,傳統物理「粒子與波動」的二分法似乎失效了。
量子時代新概念——波函數(波包)
因應這些觀察,物理學家開始用「波動力學」來解釋雙狹縫實驗,也就是薛丁格方程式(Schrödinger equation)。
「波動力學」是將所有物體都當成是「一小段波動」,也就是波函數,並寫下它如何隨著時間演化。原本的粒子現在變成像是下圖中一塊一塊的「波包」,在空間中隨著薛丁格方程式移動。
這些「波包」成功解釋了粒子如何在穿過雙狹縫後互相干涉,形成亮暗條紋。但問題是,沒有人看得到這些波函數(波包),在觀測時,看到的只有一顆顆電子通過狹縫撞在屏幕上。
雖然薛丁格所提出的方程式與運算結果完全符合實驗結果,但為什麼這樣算是對的?波函數(波包)又代表什麼?卻沒有一個很好的解釋。
波函數不是實體,而是物體的機率分布——哥本哈根詮釋
為了解釋這個問題,首先是由海森堡一夥人提出的「哥本哈根詮釋」,他們認為:波函數代表的是物體出現位置的機率分布,而薛丁格方程式規範的是機率分布如何隨時間改變。
當我們介入觀察,波函數便會依照這個機率分布隨機地塌縮至一個特定的值,這個值就是我們所觀察到的物理量。
以雙狹縫來說,穿過狹縫後的波函數產生了波動會有的干涉現象。後方的屏幕讓波函數塌縮,因此出現了一個確切的光點。至於光點會出現在哪裡,完全是機率性的,機率多寡由波函數主掌。在波峰和波谷抵銷的地方,機率很小,幾乎不會有光點出現;反之亦然。下圖可以看到個別粒子的位置看似隨機,但隨著實驗的粒子數增加,波函數的機率分布開始浮現。
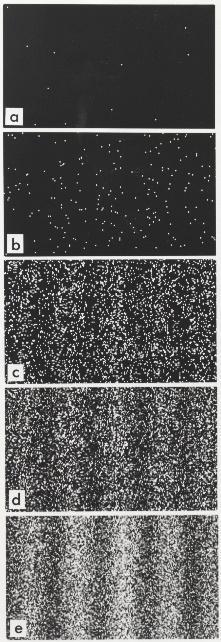
編按:哥本哈根詮釋認為,波函數涵蓋了物體落到任何地方的所有可能性,且每個可能性都有一個機率值。而薛丁格方程式算的是每一種可能性的機率變化。
在多個相同物體重複經歷相同的事件(例如電子不斷進進入雙狹縫),就會看見波函數控制物體運動過程的證據(屏幕上最後的圖形)。
至於「單個物體」為什麼會移動到某個確定的位置,以及「單個物體」實際上是怎麼移動的,基本上是不可知的,一切都是波函數的決定,因此哥本哈根詮釋就以「崩塌」,來代稱其他可能性消失的情況。
對哥本哈根詮釋的質疑
約一百年後的今天,這個詮釋已經成為主流,但當時的學界中有一部份人並不買單。
一來是因為這個說法直接擁抱了機率性,物理世界完全交由波函數塌縮的隨機過程來決定,我們能知道的只有波函數的樣貌;二來則是「塌縮」這種語焉不詳但又扮演中心角色的詞彙,讓人有一種硬湊答案的感覺。另外,人或是儀器作為觀察者的角色為何如此重要,好像也說不清楚。
為了點出荒謬之處,薛丁格搬出了他舉世聞名的貓咪。
由於原子的放射衰變也是由波函數描述,我們可以用放射性原子打造一種可以殺死貓咪的裝置,然後把貓咪跟裝置關在箱子裡。隨著時間過去,原子的狀態處於衰變和未衰變的機率分布,因此貓咪也同樣處於「死和活的機率分布」。直到觀測者將箱子打開,才能將原子和貓咪的波函數塌縮。
這個實驗和樂透開獎的情況本質上並不一樣。雖然樂透好像也是機率問題,但是每個樂透號碼球都是巨觀的、可以被古典力學描述的物體。因此,早在開獎前,每個號碼球的位置就都已經決定好了,只是沒有人能夠準確預測。
可是,原子衰變是量子的範疇。量子理論最初的發展,便是起源於光電效應和原子光譜這類小尺度世界,這些領域中的實驗觀察無法由古典力學概括,只能用波函數的機率來解釋。
而薛丁格的目標就是將微小的量子物體(原子)和巨觀的生物(貓咪)牽連在一起,試圖說明由機率分布和塌縮主宰的物理世界有多麼讓人不舒服。

在薛丁格方程式和哥本哈根學派交鋒過後的幾十年內,關於觀察和塌縮究竟是怎麼一回事,仍有許多討論。後續的許多研究,在哥本哈根的架構下,提出了修補的細節,許多人也就漸漸接受了機率性的塌縮這件事。
爾後,有另一批人馬企圖想出一種不需要機率塌縮的量子世界,其中包括不喜歡上帝丟骰子的愛因斯坦等人。他們認為粒子一直都有明確的位置與軌跡,只是其演化方式不如我們所想像,背後有不為人知的物理機制,而哥本哈根的世界觀只是統計的結果,並不是完整的圖像。
這類詮釋統稱為隱變數詮釋(hidden variable theory),歷史上有許多不同版本。不過在貝爾定理(Bell’s theorem)的相關實驗後,局域性的隱變數理論幾乎完全被排除。現今還站得住腳的隱變數理論,聲稱波函數像是電磁場一樣佈滿整個空間,能夠以特定方式引導粒子的運動軌跡。
- 延伸閱讀(貝爾定理):照出黑洞不算什麼,科學家連量子纏結都能拍到!?
全部的可能性都持續存在——多世界詮釋
這些新理論儘管在某種程度上去掉了塌縮的成分,但聽起來依然十分玄妙。在 1950 年代,有位美國物理學家艾弗雷特(Hugh Everett III)在他的博士論文中提出了全新的方案:
「大家都不要吵了,波函數中所有可能發生的機率,確實就是發生了,只是所有可能性以互不交錯的世界線同時存在。」
以貓咪為例子,當你打開箱子時,並沒有把貓咪的波函數塌縮到單一的死或活狀態,而是將原本的世界線一分為二,當中分別有一個看到死貓的你和看到活貓的你。於是,波函數永遠不需要塌縮到我們看到的單一狀態。
換句話說,這種觀點中沒有所謂「非量子」的「觀察者」來讓波函數成為現實。世界上所有的原子、貓咪、人,都被涵蓋在整個宇宙的波函數中。艾弗雷特原本的論文標題並沒有提到多重世界,而是稱之為全體波函數理論(Theory of the Universal Wavefunction)。波函數描述的不是觀察的機率分布——波函數就是本體,根據薛丁格方程式演化出各個世界線。
或許是因為太過前衛,他的這篇論文發表時,幾乎沒有引起任何討論,甚至沒什麼人花時間質疑。艾弗雷特最終抱著遺憾離開學術界,跑去五角大廈工作。所幸他的想法在十幾年後,終於在幾位支持者的努力之下,以「多世界詮釋(the many-worlds interpretation)」的名號發揚光大。
儘管一開始聽起來很難接受,但是人們發現,這種詮釋其實並不比原本的塌縮詮釋荒唐。
它同樣能夠解釋所有的實驗現象,而且比起機率性的塌縮,總體波函數可以完全遵循方程式的預測,不需要引入量子世界外的觀察者,來讓波函數塌縮至單一狀態。許多物理學家認為這是一套更簡潔的思考方法。到今天,多世界詮釋已經累積了不少聲量和支持者。
尋找多重宇宙
那麼多重世界線真的存在嗎?要找到答案恐怕不容易。如果艾弗雷特所言不假,也就是所有人和所有儀器都是總體波函數的一部份,那麼便沒有人能立於一切之外,看見總體波函數中的所有可能,或是做實驗來驗證多重世界的存在。
不過,除了量子理論的研究者之外,還有一群人也十分認真看待多重宇宙的想法。在宇宙學中,有一理論預測我們的可觀測宇宙只是顆小泡泡,身處許多其它的泡泡宇宙之中,也就是實際意義上的多重宇宙。這些宇宙不斷地處於膨脹階段,而這個理論被稱為永恆暴脹(eternal inflation)。
相較於多世界作為量子力學的詮釋,永恆暴脹是個科學理論,需要可以被驗證。照理來說,任何來自其它宇宙泡泡的訊號都跑不贏膨脹的速度,永遠無法抵達我們的可觀測宇宙。不過在膨脹初期,泡泡之間的碰撞會在宇宙背景輻射的地景上留下溫度足跡。大約十年前,科學家就在威爾金森微波各向異性探測器(WMAP)的觀測資料中,找到了四個統計上顯著的碰撞痕跡。
那我們怎麼還不出發前往其它宇宙呢?雖然在分析方法上是個振奮人心的嘗試,但還需要補足更多觀測資料才能做更好的判斷。繼 WMAP 後,普朗克衛星(Planck)也帶回了解析度高三倍的背景輻射影像,但關於多重宇宙是否真的存在,依然沒有定論。
結語
回顧歷史,隨著量子實驗的結果浮上檯面,不同的理論模型往往需要數十年來分出高下。雙狹縫實驗在 1801 年就已經完成,但多世界詮釋的誕生是 150 年後的事。正如同二十世紀初的量子物理,膨脹理論和多重宇宙都是目前發展空間很大的領域。或許還要一段時間,我們才能見證這些科幻內容成為課本中的教材。
不論結果如何,總體波函數中無限分岔的可能性,以及膨脹中的多重泡泡宇宙,都展示了科學研究的迷人之處,那就是——科學和科幻文本都一同站在人類想像力的最前端。