當現代的自造者遇上千百年歷史的多面體

柏拉圖將古典四元素：火、空氣、水、土對應到四種正多面體，並描述神使用正十二面體來排列整個天空的星座。千百年來人們不停探索多面體背後的規律，懷著對宇宙秩序的嚮往與好奇，現代的自造者則解構多面體的組成，藉由自造工具與身體感將想法化為具體。

沈岳霖老師自創工法完成各式材質創作，以雙手自造形狀近乎完美的多面體，體現古典幾何的純粹理性與極致工藝的堅定細膩，同時在教育現場帶領學生共同自造令人驚歎的大型幾何創作。此外，學生們揮灑創意將多面體裹上繽紛色彩，也充分展現數學在傳統工藝與現代想像的多面美學。

本次展覽透過「多面體自造」、「自造過程」、「關於自造者」、「多面體與建築」、「自造多面」等單元，以「多面」與「自造」為關鍵字，串聯國立後壁高中沈岳霖師生精彩創作，以「多面」向探討「自造」，呈現如何以「自造」實現「多面」。

2015年底《IMAGINARY：Infinity & Beyond 超越無限．數學印象》由德國引進臺灣，在各地掀起了一股數學藝術熱潮，讓許多人看見數學的美；延續先前的Imaginary，這次嘉義大學委託我們自行策劃數學藝術展覽《多面自造 Polyhedron Making》，想讓大家看見數學的多面姿態與自造者的驚人實踐力。

首先來介紹一下頗具巧思的展覽文宣，沿著設計好的摺線與卡榫，只用雙手就可以組出一個相當可愛的正二十面體，就算手拙如我的人也能輕鬆完成，讓人還沒進到展場內就已經體會到動手做的樂趣。

除了讓數學變得很可愛的文宣之外，展場設計也運用了六角柱這個幾何元素，擺放了連國內科學類博物館都不曾完整呈現的四大類型多面體，分別是：

1. 柏拉圖立體（Platonic Solids）：每面皆全等的正多邊形所組成的均勻凸多面體，也就是正多面體，共有5種。
2. 阿基米得立體（Archimedean Solids）：兩種以上的正多邊形為面所組成的凸多面體，可從柏拉圖立體經截角、截半等操作後構成，共有13種。
3. 卡塔蘭立體（Catalan Solids）：阿基米德立體的對偶多面體，每一面均為全等的非正多邊形，共有13種。
4. 克卜勒─龐索多面體（Kepler-Poinsot Polyhedron），由正多邊形或正星形所組成的凹多面體，每個頂點都由相同數目的邊連接。共有4種。

有了這四大類型多面體，可以理解「多面自造」的多面是什麼意思，那自造（making）呢？這樣精緻的展品竟然是自創工法並且用手工製作的，究竟是怎麼做出來的呢？

用雙手自造多面

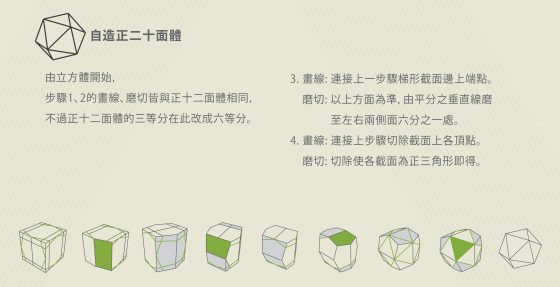
就以最常見的柏拉圖立體當作例子，現任後壁高中美工科的沈岳霖老師首先解構多面體的幾何原理，將想製作多面體的各邊投影至立方體上再畫線標記，最後再以圓盤式砂磨機將不要的塊體磨掉，就可以得到多面體啦。

這過程聽起來不難，但其實一點也不簡單，畢竟不少多面體只要稍有磨偏或是不對稱，馬上就能夠用肉眼辨識出來，這樣高超的木工技術更是連國內數學藝術大師吳寬瀛都相當驚歎。在自造過程展區中，除了自造正二十面體的實體展品（如上圖），更精美圖解四種多面體的自造步驟，包含正四面體、正八面體、正十二面體以及正二十面體，讓人一看就懂。

除了多面體之外，展場中有一件相當有趣的碎形幾何作品叫做〈YES, I DO〉，其數學原理為謝爾賓斯基四面體（Sierpinski Tetrahedron），除了可以觀察展品的光影之外，在特定的角度還可以分別看到YES和I DO呢。

看了這些有趣的作品，多面體和日常生活有什麼關聯呢？展場中有一個展區為〈多面體與建築〉，介紹正在興建中的臺南市美術館當代館，其遮蔭屋頂採用前面作品提到的謝爾賓斯基四面體；另一個與多面體有關的建築則是伊東豊雄建築博物館，建築外觀是由四種阿基米得立體組合而成。

除了看展之外，展場中設置了「自造多面」體驗區可以動手參與，雖然無法在此體驗木作多面體的減法美學，但可以藉由3D列印的加法堆疊，製作元件感受空間解謎樂趣。此外，自造者使用的材料也在展場中以立方體的型式展示，包括雲杉、酸枝、柚木、檜木、烏心石，以多元面向探討自造。

潛心研究多面體，多做少說的木工國手

身為《多面自造》的策展人之一，我們為了這次展覽專訪後壁高中沈岳霖老師［1］，一到後壁高中木工教室，沈岳霖老師就拿出了朋友種的冷泡烏龍茶請我們喝，實在是這間沒有裝設空調教室的絕佳飲品啊。

沈岳霖老師畢業於公東高工木工科，這可是間在海岸山脈留下教育傳奇的學校［2,3,4］，出產許多在世界技能競賽奪得獎牌的木工國手，沈岳霖老師為其中之一。在那個年代，成為國手是一件比聯考還要難上許多的事情。

從高一不停參加競賽，到全國賽至選拔賽一路過關斬將，終於在20歲的時候成為木工國手，並且在1985年代表台灣參加在日本大阪舉辦的國際技能競賽，獲得門窗木工銅牌也就是世界第三，保送至高雄師範大學工業科技教育系。

不過沈老師的人生也不是全是一帆風順，他也曾經不知道為什麼要念書，考上光武工專電機科後兩個月就休學。某次和朋友去台東玩發現公東高工盛產國手，他們出國比賽拿了許多獎牌回來，便一心嚮往成為能夠保送大學的國手，因此重考進入公東高工就讀，進入公東前也只在國中的工藝課接觸過一點木工。

從公東開始過著選手訓練的生活，加上長期居住在鄉下的緣故，逐漸養成獨自工作、只做不說的習慣，以及低調沉穩的性格。在後壁高中的木工教室內，沈老師不疾不徐地解說木工備料流程；倒是進行採訪工作的我狂冒汗，一直倒冷泡茶來解渴。

訪問過程中提到多面體的時候，沈老師的眼神亮了起來，畢竟這是他順利融入教書工作的多年興趣。一開始的時候是以魯班鎖當作木工課的素材，後來發現多面體易於變化造型適合發展為教材，閒暇時便經常思索多面體構件的尺寸和角度，還曾經在斗南老家夢到菱形三十面體的角度，花費大量時間解開複雜問題獲得的成就感更使他樂此不疲。

沈岳霖老師並不以藝術家自居，只是喜歡動手做的過程，也喜歡設計出可以讓別人玩的玩具，對他來說是人生一大樂趣。更幸福的是，能把興趣融入工作帶到教育現場與學生共同自造；與沈老師經常交流數學的林義強老師認為，這是沈老師做過最有價值與最困難的事情。

像是展場中這一件師生共同完成的作品《截角菱形三十面體》（如上圖），是沈老師看見Philippe Dubois的創作Icosahedron Frequency 2，透過解構多面體、設計卡榫、製作模形的過程，以師生共同自造與組裝的方式重現作品。

每年沈老師皆會更新課程教材，勇於在課堂上挑戰新的大型作品；除了製作木工之外，沈老師讓後壁高中美工科的學生自由創作，讓千百年歷史的多面體加上現代的想像後變得相當可愛。

我們策這一檔展覽，並不是要強調數學有多實用，或是介紹多面體的歐拉公式，而是想讓大家看見數學有趣、令人著迷的一面，也想將沈岳霖老師多年來對於幾何的熱愛以及自造者精神(maker)傳達給大家。

同時在此預告十二月初會有臺灣數學藝術大師吳寬瀛老師的積木幾何創作展，原班策展團隊同樣在嘉義大學，要讓大家看見〈轉幾‧轉積‧轉機〉，請大家拭目以待！

＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

《多面自造：沈岳霖師生幾何創作展》展覽資訊

地點：國立嘉義大學蘭潭校區圖書資訊館（嘉義市東區學府路300號）

展期：2017/10/23─11/24 週一至週六 09:00 ~ 17:00 週日 14:00 ~ 17:00

臉書粉絲頁：多面自造：沈岳霖師生幾何創作展

策展人：余歡庭、林家妤

聯絡人：國立嘉義大學應用數學系嚴志弘主任

參考資料

1. 沈岳霖老師部落格與臉書
2. 范毅舜，公東的教堂：海岸山脈的一頁教育傳奇，2012
3. 黃清泰，瑞士學徒制教育在公東：一位老校長引導的學習革命，2017
4. 莊文毅，台東木工發展史卷一：東海岸木工傳奇，2017

2013 年國際數學界最轟動的新聞，應屬中國留美學者張益唐在孿生質數問題上所作出的突破。他個人的經歷更增加了整件事的傳奇性。

張益唐雖然是北大數學系的高材生，但是 37 歲從美國普渡大學拿到博士學位之後，因與指導教授意趣不合，一時在學界無法發展，多年靠打工餬口。1999 年才好不容易至新罕布夏大學數學系任講師。在張益唐長期不得意的歲月裡，他雖然沒有發表什麼數學論文，但是也不曾喪失志氣，還是堅持研究自己喜歡的數學問題。

張益唐在 58 歲暴得大名，各種獎項與頭銜接踵而來，在最是少年逞英豪的數學世界裡，真成為一個異數。英國數學家哈代在他著名的小冊子《一個數學家的辯白》裡曾說：「我不知道有任何一項數學的主要進展，是由超過五十歲的人所啟動。」張益唐正好給哈代的偏見一個反例。

張益唐研究的是關於質數的性質。

一個自然數 p 是質數（也稱為素數）的條件有二：其一，p 大於 1；其二，除了 1 與 p 自己之外，沒有別的自然數能整除 p。全體質數可以從小到大排成一個數列 2, 3, 5, 7, 11, 13, …，通常把排在第 n 個位置的質數記作 pn。如果 pn 與 pn+1 相差為2，則稱質數對 (pn, pn+1) 為一對孿生質數，例如 3 與 5，5 與 7，11 與 13。

「孿生質數猜想」就說這樣的質數對有無窮多組。因為古希臘的歐幾里得在他的巨著《原本》裡，曾經證明質數有無窮多個，所以有人以為也是歐幾里得最先提出孿生質數猜想。其實不然，目前從文獻中所見， 1879 年英國數學家格萊舍（James Whitbread Lee Glaisher）在《數學信使》（Messenger of Mathematics）雜誌上的一篇文章，才是第一次將孿生質數猜想見諸文字。

張益唐的大突破是證明有無窮多組質數對 (pn, pn+1) 使得 pn 與 pn+1 相距不超過 7 千萬。

為什麼這是一個大突破呢？因為在張益唐之前，不管給出什麼固定數 m，完全不知道相差在 m 之內的質數對，到底是有限多個還是無窮多個。自從 2013 年 5 月他的成就在國際媒體上廣為流傳之後，世界上很多數學家努力要把 7千萬的差距往下壓縮，目前已經改善到 246 之內。但是距離孿生質數猜想所需的 2，還有巨大而艱困的鴻溝。

一般人從媒體得知張益唐對數學做出了重大貢獻，可能會好奇問他的結果有什麼用？這裡「用」當然是指實際的應用。其實，他的成果目前還只有純學術價值，與國計民生毫不相干。自從古希臘人辨識出質數，在兩千多年的時間裡，除了數學家關心質數外，質數一直缺乏任何應用價值。二十世紀電腦發達之後，才利用因數分解成質數的超級困難特性，產生了某些幾乎無法有效破解的密碼系統，廣泛的應用到金融、通信、資料保密上。

在中國古算裡缺席？

一個基本的數學概念，經歷了兩千多年的滄桑，才顯現出它的實用價值，這不是一件平凡的成就。因此，我們不得不佩服希臘人研究質數的真知灼見，並且感嘆十八世紀前的中國傳統數學裡卻不見質數的蹤跡。質數為什麼會在中國遲來報到？實在是一個令人費解的現象。

歐幾里得的《原本》約在西元前 300 年左右成書，是古希臘數學集大成之作。第七卷討論數的性質，是使用幾何的觀點來理解數。也就是從「單位」的概念出發，以度量直線段的方式引入「數」。第七卷定義 2 說「一個數是由許多單位合成的。」因此，1 代表單位而不算作「數」。定義 11 說「質數是只能為一個單位所量盡者。」定義 16 說「兩數相乘得出的數稱為面，其兩邊就是相乘的數。」所以質數只能是線，而不能稱為面。

從這些定義可看出來，古希臘人所謂的「數」是依附在幾何的體系裡而得以操作。中國古代缺乏像《原本》這種按照邏輯次序鋪陳結果的數學書，通常是以解決實際問題的風貌來書寫，因此不太可能探討與闡述「數」的純粹性質。

例如，以《九章算術》為代表的中國古算裡，數字是與矩形、直角三角形的面積緊密相連結，但卻沒有像希臘人那樣分辨，有些數是可以表現為面，而有些數卻不可以。

也許古代中國缺乏一項歐幾里得所擁有的知識背景，因而造成了雙方關注問題的差異。古希臘有一位重要的哲人德謨克利特（Democritus），他主張萬物皆由不可分割的「原子」所構成。在「原子論」的知識背景下，數目 1 就不會與其他數目等量齊觀了，1 是「單位」，是數的「原子」。

中國古代沒有明確的「原子論」，《墨子．經說下》所說：「非半，進前取也。前，則中無為半，猶端也。」其中切得不能再切的「端」在《墨子．經說上》解釋為「端，體之無序而最前者也。」也只是類似「原子」的概念，並未發展到德謨克利特的思想程度。「原子論」思想的欠缺，或許是質數在中國古算裡缺席的因素之一。

難以望其項背

康熙敕編的《御製數理精蘊》（簡稱《數理精蘊》）是融合中西數學的百科全書，其中將質數譯為「數根」，並且在附表〈對數闡微〉中列有質數表。雖然質數已經在中國現身，但是數學家並沒有感到相見恨晚而深入探討。

晚清數學名家李善蘭在翻譯歐幾里得《原本》後九卷時，第一卷第一界說為：「數根者唯一能度而他數不能度」，也把質數翻譯成「數根」。

李善蘭很可能受《數理精蘊》的影響，而去研究判別給定數是否為質數的方法。英國傳教師偉烈亞力（Alexander Wylie）將其中一法，以給編輯的信公布在香港一家英文雜誌上，其敘述為「以 2 的對數乘給定的數，求出其真數，以 2 減同數，以給定數除餘數，若能除盡，則給定數為質數；若不能除盡，則不是質數。」

此命題常被稱為「中國定理」，其實是歐洲早已知道的「費馬小定理」的逆命題，該定理斷言若 p 為質數，則 2p − 2 ≣ 0 (mod p)。

其實李善蘭的方法並不永遠正確，例如：2341 − 2 是 341 的整倍數，但是 341 = 11 × 31 並不是一個質數。1872 年李善蘭在《中西聞見錄》報刊發表了〈考數根法〉一文，成為清末關於質數研究的重要成果，但是他並沒有收錄「中國定理」，應該是他已經知道命題並不為真。

要知道李善蘭與高斯的生命是有重疊的時期，因此當西方以質數為基礎所建立的數論，已經繁複深刻美不勝收之時，也許連李善蘭都不曾完全清楚中國落後的程度是多麼巨大！