最自戀的乘方開方數字團體——位數根的快樂夥伴（二）

本文與 高柏科技 合作，泛科學企劃執行。

當我們談論能擊敗輝達（NVIDIA）、Google、微軟，甚至是 Meta 的存在，究竟是什麼？答案或許並非更強大的 AI，也不是更高速的晶片，而是你看不見、卻能瞬間讓伺服器崩潰的「熱」。

 2024 年底至 2025 年初，搭載 Blackwell 晶片的輝達伺服器接連遭遇過熱危機，傳聞 Meta、Google、微軟的訂單也因此受到影響。儘管輝達已經透過調整機櫃設計來解決問題，但這場「科技 vs. 熱」的對決，才剛剛開始。 

不僅僅是輝達，微軟甚至嘗試將伺服器完全埋入海水中，希望藉由洋流降溫；而更激進的做法，則是直接將伺服器浸泡在冷卻液中，來一場「浸沒式冷卻」的實驗。

但這些方法真的有效嗎？安全嗎？從大型數據中心到你手上的手機，散熱已經成為科技業最棘手的難題。本文將帶各位跟著全球散熱專家 高柏科技，一同看看如何用科學破解這場高溫危機！

運算=發熱？為何電腦必然會發熱？

這並非新問題，1961年物理學家蘭道爾在任職於IBM時，就提出了「蘭道爾原理」（Landauer Principle），他根據熱力學提出，當進行計算或訊息處理時，即便是理論上最有效率的電腦，還是會產生某些形式的能量損耗。因為在計算時只要有訊息流失，系統的熵就會上升，而隨著熵的增加，也會產生熱能。

換句話說，當計算是不可逆的時候，就像產品無法回收再利用，而是進到垃圾場燒掉一樣，會產生許多廢熱。

要解決問題，得用科學方法。在一個系統中，我們通常以「熱設計功耗」（TDP，Thermal Design Power）來衡量電子元件在正常運行條件下產生的熱量。一般來說，TDP 指的是一個處理器或晶片運作時可能會產生的最大熱量，通常以瓦特（W）為單位。也就是說，TDP 應該作為這個系統散熱的最低標準。每個廠商都會公布自家產品的 TDP，例如AMD的CPU 9950X，TDP是170W，GeForce RTX 5090則高達575W，伺服器用的晶片，則可能動輒千瓦以上。

散熱不僅是AI伺服器的問題，電動車、儲能設備、甚至低軌衛星，都需要高效散熱技術，這正是高柏科技的專長。

「導熱介面材料（TIM）」：提升散熱效率的關鍵角色

在電腦世界裡，散熱的關鍵就是把熱量「交給」導熱效率高的材料，而這個角色通常是金屬散熱片。但散熱並不是簡單地把金屬片貼在晶片上就能搞定。

現實中，晶片表面和散熱片之間並不會完美貼合，表面多少會有細微間隙，而這些縫隙如果藏了空氣，就會變成「隔熱層」，阻礙熱傳導。

為了解決這個問題，需要一種關鍵材料，導熱介面材料（TIM，Thermal Interface Material）。它的任務就是填補這些縫隙，讓熱可以更加順暢傳遞出去。可以把TIM想像成散熱高速公路的「匝道」，即使主線有再多車道，如果匝道堵住了，車流還是無法順利進入高速公路。同樣地，如果 TIM 的導熱效果不好，熱量就會卡在晶片與散熱片之間，導致散熱效率下降。

那麼，要怎麼提升 TIM 的效能呢？很直覺的做法是增加導熱金屬粉的比例。目前最常見且穩定的選擇是氧化鋅或氧化鋁，若要更高效的散熱材料，則有氮化鋁、六方氮化硼、立方氮化硼等更高級的選項。

典型的 TIM 是由兩個成分組成：高導熱粉末（如金屬或陶瓷粉末）與聚合物基質。大部分散熱膏的特點是流動性好，盡可能地貼合表面、填補縫隙。但也因為太「軟」了，受熱受力後容易向外「溢流」。或是造成基質和熱源過分接觸，高分子在高溫下發生熱裂解。這也是為什麼有些導熱膏使用一段時間後，會出現乾裂或表面變硬。

為了解決這個問題，高柏科技推出了凝膠狀的「導熱凝膠」，說是凝膠，但感覺起來更像黏土。保留了可塑性、但更有彈性、更像固體。因此不容易被擠壓成超薄，比較不會熱裂解、壽命也比較長。

OK，到這裡，「匝道」的問題解決了，接下來的問題是：這條散熱高速公路該怎麼設計？你會選擇氣冷、水冷，還是更先進的浸沒式散熱呢？

液冷與 3D VC 散熱技術：未來高效散熱方案解析

傳統的散熱方式是透過風扇帶動空氣經過散熱片來移除熱量，也就是所謂的「氣冷」。但單純的氣冷已經達到散熱效率的極限，因此現在的散熱技術有兩大發展方向。

其中一個方向是液冷，熱量在經過 TIM 後進入水冷頭，水冷頭內的不斷流動的液體能迅速帶走熱量。這種散熱方式效率好，且增加的體積不大。唯一需要注意的是，萬一元件損壞，可能會因為漏液而損害其他元件，且系統的成本較高。如果你對成本有顧慮，可以考慮另一種方案，「3D VC」。

3D VC 的原理很像是氣冷加液冷的結合。3D VC 顧名思義，就是把均溫板層層疊起來，變成3D結構。雖然均溫板長得也像是一塊金屬板，原理其實跟散熱片不太一樣。如果看英文原文的「Vapor Chamber」，直接翻譯是「蒸氣腔室」。

在均溫板中，會放入容易汽化的工作流體，當流體在熱源處吸收熱量後就會汽化，當熱量被帶走，汽化的流體會被冷卻成液體並回流。這種利用液體、氣體兩種不同狀態進行熱交換的方法，最大的特點是：導熱速度甚至比金屬的熱傳導還要更快、熱量的分配也更均勻，不會有熱都聚集在入口（熱源處）的情況，能更有效降溫。

整個 3DVC 的設計，是包含垂直的熱導管和水平均溫板的 3D 結構。熱導管和均溫板都是採用氣、液兩向轉換的方式傳遞熱量。導熱管是電梯，能快速把散熱工作帶到每一層。均溫板再接手將所有熱量消化掉。最後當空氣通過 3DVC，就能用最高的效率帶走熱量。3DVC 跟水冷最大的差異是，工作流體移動的過程經過設計，因此不用插電，成本僅有水冷的十分之一。但相對的，因為是被動式散熱，其散熱模組的體積相對水冷會更大。

從 TIM 到 3D VC，高柏科技一直致力於不斷創新，並多次獲得國際專利。為了進一步提升 3D VC 的散熱效率並縮小模組體積，高柏科技開發了6項專利技術，涵蓋系統設計、材料改良及結構技術等方面。經過設計強化後，均溫板不僅保有高導熱性，還增強了結構強度，顯著提升均溫速度及耐用性。

隨著散熱技術不斷進步，有人提出將整個晶片組或伺服器浸泡在冷卻液中的「浸沒式冷卻」技術，將主機板和零件完全泡在不導電的特殊液體中，許多冷卻液會選擇沸點較低的物質，因此就像均溫板一樣，可以透過汽化來吸收掉大量的熱，形成泡泡向上浮，達到快速散熱的效果。

然而，因為水會導電，因此替代方案之一是氟化物。雖然效率差了一些，但至少可以用。然而氟化物的生產或廢棄時，很容易產生全氟/多氟烷基物質 PFAS，這是一種永久污染物，會對環境產生長時間影響。目前各家廠商都還在試驗新的冷卻液，例如礦物油、其他油品，又或是在既有的液體中添加奈米碳管等特殊材質。

另外，把整個主機都泡在液體裡面的散熱邏輯也與原本的方式大相逕庭。如何重新設計液體對流的路線、如何讓氣泡可以順利上浮、甚至是研究氣泡的出現會不會影響元件壽命等等，都還需要時間來驗證。

高柏科技目前已將自家產品提供給各大廠商進行相容性驗證，相信很快就能推出更強大的散熱模組。

本文由 微星科技 委託，泛科學企劃執行。

• 作者 / 曾繁安

人類總會不由自主地被閃閃發光的事物吸引，取名時加上「黃金」二字，好像就能讓身價大漲，變得受歡迎。不管是黃金海岸、黃金地段、黃金右腳、 黃金奇異果，黃金獵犬、黃金脆薯、黃金盔甲、黃金流沙包、黃金開口笑（大誤）……人們用黃金形容所有美好的事物，連「比例」也一樣。「黃金比例」被譽為最美好的比例，你一定聽聞過，如果人的臉蛋身體或畫作構圖越接近黃金比例，就越迷人的説法。然而一個數字比例，怎麼會和美學扯上關係？

人類探究黃金比例的歷史，可追溯至兩千多年前……

古希臘時代大約公元五百多年前，癡迷於數學的畢達哥拉斯，認爲數學可以解釋世上一切事物。他的教學吸引了一群熱心的追隨者，被稱爲畢氏學派。在旁人眼裏，畢氏學派恐怕是一群怪人：恪守極爲嚴格的生活條規，不可吃肉和豆類，還會進行高强度記憶力訓練和三省吾身等等。但畢氏學派對數學幾近狂熱崇拜，尤其對數字 5 和五角星形的迷戀，使他們成爲史上最早接觸黃金比例分割的一群人。將構成五角星形的線段分割，由短至長排列，把最短的兩條線段相加，恰恰等於第三條線段長；把第二短和第三短的線段相加，也會等於第四條線段，依序如是，顯示出黃金比例的奇妙！不過，他們並沒有進一步為這個神奇的發現加以解釋、定義和命名。

一直到公元前三百年，歐基里德所著的《幾何原本》問世，才有了對黃金比例最早的系統性論述。但你知道嗎？歐基里德也根本沒說過「黃金比例」一詞。後世所謂的「黃金比例」，其實是出現在《幾何原本》第四章的「極限與均值比例」（Extreme and mean ratio）。歐基里德對這個比例的說明如下：

“A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser.”

（一條線段如果切在「極限與均值比例」上，則線段的全長與較長分割段的長度比例，和較長分割段與較短分割段的長度比例相等。）

大家常常挂在嘴邊的黃金長寬比 1.618 ，就是從上圖的比例計算而來。只要把較短的線段 b 定義成 1 個單位，較長的線段 a 定義成 x 單位，再用一點國中數學上過的一元二次方程式，就能算出解答為 1.6180339887…… 或 0.6180339887…… 這兩個看～～～不到盡頭的無理數，都可被視爲黃金比例之值。就像另一位大名鼎鼎的無理數——圓周率，是以 「π」來表示，黃金比例也有自己的符號，叫做「φ」。「φ」一般念作 “ fai ” ，跟「π」押同韻，但捍衛正統希臘文念法的人可能會堅持念作 “ fee ”。

當初歐基里德只説了這麽多，純粹是為了解釋數學幾何上的意義。但他想也想不到的是，這個「極限與均值比例」，會變成美的代言人，帶給未來人類無限遐想的空間。

數學與人文藝術匯集，文藝復興時期的「神聖比例」

現代人熟知的「黃金比例」一詞，一直到 1830 年代左右才被廣爲流傳。在此之前，它的地位曾被提升到更崇高、神聖的位置。文藝復興時期，被稱為「會計學之父」的數學家兼方濟會修士——盧卡．帕西奧利（Luca Pacioli），出版了名叫《神聖比例》（Divina scalee）的著作。他從歐基里德定義的「極限與均值比例」出發，對正多面體和半正多面體的性質做討論。

帕西奧利在研究「極限與均值比例」時深受啟發，開始與他熟悉的神學進行連結。他發現這個比例中提到的三個線段（全長、長邊、短邊），都在描述同一條線，像極了基督教的神學觀，既聖父、聖子和聖靈是三位一體。而這個比值之解的無理數，所具備無法窮盡的性質，就如同凡人無法理解全能無限的上帝般，兩個線段之比例是相等的（全：長 = 長：短），則代表神永恆的不變性與無所不在的屬性。

從數學上看見神學解釋的帕西奧利，遂將「極限與均值比例」改稱為「神聖比例」。他在著作中進一步以「神聖比例」分析古希臘羅馬建築與人體結構的比例。在他看來，被神所創造的人類，其軀幹比例也隱含了「神聖比例」。這些內容更深地加強了「神聖比例」與「美」之間的連接。

此後，「神聖比例」便與「宗教」和「美」脫離不了關係。帕西奧利對純數學理論進行宗教哲學解讀的突破，成功地讓這個神奇的比例跨出數學界的舒適圈，成為數學家、神學家與藝術家之間共同的話題，後來更在討論中逐漸演變成後世蔚為流行的「黃金比例」。帕西奧利可説是打開「黃金比例」知名度，背後不可或缺的功臣。

宇宙誕生以來就存在？藏在大自然中的密碼竟是「黃金數列」

儘管吉薩金字塔和帕特農神殿是否依照黃金比例建造，數學界和藝術界還在爭辯不休，但實際上不需要人爲設計，大自然本身就蘊藏著黃金比例的美麗。以描述「兔子生兔子」問題而聞名的費波那契數列（Fibonacci number），可説是黃金比例的孿生手足。費波那契數列第零項是 0，第一項是 1，從第二項以後的值，就是前兩項加起來的和，所以依序會是：

1、1、2、3、5、8、13、21、34、55、89、144、233……

文藝復興後期鼎鼎大名的天文學家克卜勒（Johannes Kepler）發現，把費波那契數列的後一項除以前一項的值的話，會是 1 / 1 = 1， 2 / 1 = 2，3 / 2 = 1.5，5 / 3 = 1.67， 8 / 5 = 1.6， 13 / 8 = 1.625， 21 / 13 = 1.615…… 計算到這裏，你是不是也察覺到其中奧妙？隨著數列遞進繼續相除，這個值竟會越來越趨近於黃金比例！也因此，費波那契數列的別名就叫做「黃金數列」。

大自然中的植物，其實都是深諳造物奧義的數學大師。試著數一數雛菊的花瓣數量，你會發現它們恰好都是 13、21 或 34 的費波那契數。葉子與葉子之間要怎麽喬位子，才不會擋住彼此吸收陽光？玫瑰的花瓣要如何排列，才會顯得漂亮對稱？松果上的種子要怎麽生長，才可以有效利用有限的空間？這些問題的答案通通都是：旋轉角度的比值（以 360° 為分母）要符合黃金比例！

不只是植物界，無論是鸚鵡螺貝殼的生長、鷹隼迫近獵物的飛行軌線，抑或衛星圖上熱帶氣旋的外觀，就連宇宙中漩渦星系的旋臂，都呈現遵循黃金比例的螺線。從小至可一手掌握的貝殼，大至遙遠光年之外的星系，都藏著黃金比例的身影。大自然對這個奇妙比值的鍾愛，讓科學家着迷不已。

有生命的動植物和無生命的氣旋或星系，都不約而同服膺於一個神奇的比值，展現一種似乎自世界誕生以來就存在，難以撼動、一致而規律的美。同屬於大自然一份子的人類，也不停在各樣的建築或藝術品中追尋，渴望證明黃金比例與美的相關性。然而即使是世人眼中曠世巨作的大衛像，也沒辦法百分百貼近黃金比例，畢竟誤差永遠不能被全面消除，更別忘了有限的我們也無法窮盡無限的 φ 。正因爲黃金比例是一種人類無法徹底掌握的美，才迫使我們得以在追求美的道路上，不停努力地前進，再前進。

連自然都青睞的「黃金比例」近乎是「美」的同義詞。而我們的身邊，又有什麼東西用到黃金比例呢？

沒錯！就是這台 Creator Z16 筆記型電腦。

採用 16 : 10 螢幕的 Creator Z16 ，比市售的 16 : 9 螢幕多了 11% 的可視空間，創作更加自由寬廣。此外，16 : 10 ( 1.6 )也非常接近黃金比例（ 1.618 ），讓你在創作時，感受蘊含萬物奧秘、數學家兩千多年來淬鍊的「美」。

本著以人爲本的設計理念， Creator Z16 的觸控面板讓人可更直覺操作，隨時揮灑靈感。 90 Whr 的大容量電池搭配快充功能和 15.9 mm 纖薄金屬打造的 2.2 kg 機身，可完美配合現代人隨時行動隨地工作的步調。以 True Pixel 顯示技術打造的 QHD+ 超高畫質面板，加上獨家 True Color 技術於出廠前進行色彩校正，可以精準呈現璀璨畫面。

想堅持你對生活的美學，又不想放棄實用主義的追求？小孩子才做選擇，你可以通通都要！就讓融合黃金比例又兼具堅强實力的 Creator Z16，成為你的繆思女神吧！

現在購買 Creator Z16 加贈價值 2190 元 Microsoft 365 個人版一年期！登記再抽潮到出水的 Porter 托特包，這麼好康還不快點到賣場逛逛！

參考文獻

• 作者／大衛．翁弗拉許；譯者／林柏宏

科學的起源：以真實性質的角度來理解自然

二十世紀物理學家理查． 費曼（Richard Feynman，1918-1988）認為，當代物理學奠基於巴比倫人的數學方法，他們會以數學的方式來闡述問題，這種經驗能夠讓人學會歸納，進而發現自然原理。歐幾里得（Euclid ofAlexandria，西元前三世紀中期到西元前 285 年）的治學方法則與此相對，這位希臘思想家運用基本的邏輯規則，從我們稱為公設的基礎事實推導出更多複雜的定理。

在大約西元前三百年時，歐幾里得的方法很流行，而他的演繹法發源於更早的幾世紀前，當時的希臘思想家剛開始大膽地以真實性質的角度來理解自然。

對於月亮、太陽與眾行星性質的了解要真正有所進展，希臘的天文學家就得接受量化的方法。他們會需要巴比倫人研究天文的方法，包含實際數學運算，以及從單調的天象觀測中蒐集大量資料。他們的研究必須將這些資料融合希臘文化特有的、探討本質的思維。這種思維是從西元前六世紀的愛奧尼亞人社群開始的。

愛奧尼亞地區位於今日土耳其西部沿岸的城市與島嶼，最早開始推斷大自然是可探究、可預測的希臘人都來自這一帶，他們認為大自然的運作與眾神的意志無關。這種去除神祕面紗的世界觀由米利都的泰利斯起頭，從而解放了愛奧尼亞人的思考，開始為自然現象提出物理學的解釋模型，對科學的進步發揮了重要作用。

然而，希臘世界另一邊的哲學家都反對泰利斯的論點，這些哲學家的根據地是位於南義大利的希臘殖民地─大希臘（Magna Grecia）。

在這場論爭裡，一些大希臘區的哲學家其實是最早發現月亮是球形而非一圓盤的人，有一批大希臘的人還引進了會讓希臘天文學突飛猛進的數學知識。但是，大希臘區並無科學思維，這裡的人高張神祕主義，鄙視實證精神，影響力最大的神祕主義團體還掩蓋、打壓與其主張相左的新發現。

諷刺的是，這個神祕主義勢力團體的創始人，出生於愛奧尼亞區中心地帶薩摩斯島（Samos）的畢達哥拉斯（Pythagoras，約西元前 570-495），其實就學於泰利斯門下，並由此展開他的學術之路。

泰利斯預測日食，阻止戰爭

要是西元前二千六百年就有諾貝爾和平獎，肯定會頒發給米利都的泰利斯。

他出生時，正是巴比倫文明崛起，催生出前所未有的知識創發活躍期，他也漸漸愛上數學與天文學。愛奧尼亞隸屬於呂底亞王國（Lydian），不過泰利斯或許去過巴比倫，不然就是取得了巴比倫的天文學文獻。不管是哪種情形，泰利斯都認識到日食與月食的沙羅週期，這與他的想法不謀而合，他本來就認為神明與自然無涉。

當時呂底亞正與其敵對國之一，米迪亞（Media）交戰，泰利斯知道雙方指揮官都是迷信的人，便提出警告說，眾神要求他們休兵，並且會在西元前五百八十五年春季的某一天使太陽暗下來，以表明神意，其實泰利斯根據沙羅週期進行計算後，已經得知這一天應該會發生日食。

儘管泰利斯自己未察覺，但當他如此運用沙羅週期時，實際上計算的正是月球在太陽前方的移動。總之，日食確實出現了，戰事也平息了，泰利斯在愛奧尼亞聲名大噪，想向他學習自然研究的人蜂擁而至，其中一位就是從薩摩斯島搭船前來的畢達哥拉斯。

當時的米利都是個富庶的港口城市，當地的希臘居民不願向帝國統治者效忠，他們獨立自主，擁抱新知，或許是因為常從各地的航海貿易商口中得知新觀念，長此以往，泰利斯與其他米利都人的思考方式開始變得新穎激進。

比方說，他們認為地震是由於海中巨浪擊打陸地，土地陸塊是來自海水淤積堆造而成。這些關於自然的解釋終究會被證明並不正確，但重要的是，當時他們的想法和其他地方的人不一樣，他們的想法是可以接受驗證、有可能被否證推翻的，與那些虛無縹緲的神明無關。

泰利斯和在他之後的愛奧尼亞人之所以與眾不同，乃在於他們斷定，認識自然是可行的，可以接受觀察與分析─ 而且，對於他們之中某些人而言，也能透過試驗實證。

為封口無理數的發現而殺人的畢達哥拉斯

薩摩斯的畢達哥拉斯是目前已知世上最早指出月亮是球狀的第一人，他會這麼想或許一開始源自觀察的結果，例如發現月球明暗分界線（lunarterminator）是彎曲的，這道線區分了月球被照亮與未被照亮的兩部分。

畢達哥拉斯畢竟是泰利斯的學生，而且比同時代的人更早認出晨星（the MorningStar）與暮星（the Evening Star）是同一顆物體─ 金星。這種認知來自於觀察，雖然畢達哥拉斯後來排斥觀測，轉而堅持藉由純粹的思索即可了解宇宙。

旅居埃及多年，又去了巴比倫之後，畢達哥拉斯帶來了一項定理，直角三角形斜邊圍成的正方形面積，等於兩短邊各自圍成正方形的面積和。這不是他自己想出來的，埃及人與巴比倫人早將這觀念實際運用在生活中好幾百年了，巴比倫甚至發展出三角學這門數學。無論如何，由於畢達哥拉斯將這個定理引介給希臘人，未來幾世代探究大自然所需的數學知識才有機會出現。

但對畢達哥拉斯而言，數學不僅是工具，而是宗教信仰。

球狀月亮的想法只是畢達哥拉斯兄弟會神祕思想的一部分，畢達哥拉斯在位於義大利的克羅敦殖民地（the Croton colony）創立了這支教派。畢達哥拉斯教徒主張天界的「星球和諧」，認為月亮與其他星體不只是球形，而且是完美球形，繞著絕對的圓旋轉，每顆星球會產生特定的音符。再加上畢達哥拉斯輕視觀測法，凡是和其完美和諧觀念牴觸的新發現都一貫打壓。

其中一例是他的學生發現數字 2 開平方根會得到無理數，也就是無法化作分數，不能以兩個整數做為分子與分母來表示。謠傳畢達哥拉斯為了封口，謀殺了那個學生。

但他並不需要依靠暴力來提倡自己的學說。不久後，柏拉圖（Plato，約西元前 427-347）將熱心採納畢達哥拉斯的神祕主義，包含那些完美球形、圓形軌道、對觀察實測的輕蔑，以及阻撓接下來幾世紀科學進展的一切花俏玩意兒。

採納實證主義的亞里斯多德

和他的老師柏拉圖比起來，亞里斯多德比較有科學精神。

雖然兩人的出發點都是想將畢達哥拉斯、巴門尼德提倡的這類神祕主義哲學與愛奧尼亞人的自然主義整合在一起，柏拉圖終究傾向了神祕主義，亞里斯多德則對愛奧尼亞思維更有好感。若提到愛奧尼亞的實證主義（empiricism）── 主張知識必須透過感官作用的經驗才能取得，兩人的分歧會特別明顯。

愛奧尼亞人泰利斯觀察尼羅河的沉積土層後，做出了假設，認為全世界的大塊陸地都是經由類似過程，從一原始大洋中形成的。而泰利斯的學生、米利都的阿那克西曼德（Anaximander of Miletus，西元前 610-545）觀察幼魚和人類的差異，並在看過化石骨骼後，構想出早期版本的生物演化假說。綜合他們的所見所聞，愛奧尼亞人了解到，大自然不停地在變動。

亞里斯多德在研究如生物這一類地球上的物質時，大致上採納愛奧尼亞式的實證主義與變化觀念，可是一旦主題來到天象，他就表現出神祕主義的遺緒。畢達哥拉斯有個很妙的想法，認為天上的星體都是繞著正圓形軌道轉的完美球形，亞里斯多德深受此思想荼毒，同時還採用巴門尼德的主張，認為萬物恆定不變，結果形成了以下觀點：

星星、太陽與行星都是恆久不變的，有永遠固定的幾何形狀，地球是墮落不潔的，也因此不完美。違背這完美理念的還有月球表面的暗黑地貌，亞里斯多德對此的解釋是，月球和地球走太近了，太靠近存在於地表上的汙染，指的就是人類和其他生命形式。

——本文摘自《月球之書》，2019 年 9 月，時報出版。

今天來聊聊位數根的第二位快樂夥伴，數字的自戀組合團體——乘方開方表的故事。為什麼說乘方開方表是數字的自戀組合團體呢？平方是自己乘上自己自戀二次方（powers of 2），立方是自己乘自己再乘自己（powers of 3），總共要乘三次難道還不夠自戀嗎？

很早以前，有一天一個就讀國中二年級的少年在無聊的早自習差點打起瞌睡，心血來潮向老師借了一本數學課本，後面的附錄有著一個密密麻麻的表格，裡頭寫著數字 1, 2, 3, …, 100，還有他們的平方數 1, 4, 9,…,10000 與立方數 1, 8, 27, …, 1000000。大概是長這個樣子：

表 1：沒有開方的乘方開方表（節錄）

這位少年不知道怎麼回事，動手計算了 N² 那一欄數字的位數根，看到 25 就直覺地把 2 加上 5 得到 7。不算不知道，一算就驚為天人（？）他驚奇地發現新的位數根數列有規律，不斷重複 1, 4, 9, 7, 7, 9, 4, 1, 9 這 9 個數字，一直到 100 都遵循著如此的規律，就像是一串咒語逃不出位數根的手掌心。

那 N³ 的位數根會不會也有規律？這次重複的是三個數字 1,8,9。那接下來的四次方、五次方一直到 n 次方（powers of n），也會有規律吧！？有了這麼多 powers 和咒語，可以召喚金剛戰士（Go Go Power Rangers！）的好朋友智多星來解惑嗎？雖然智多星是個遇到事件會呀呀叫的機器人，可現在的機器可以幫忙做很多事情，計算數字這種瑣碎的事情就交給計算機了。

發現這件事之後少年異常興奮睡意完全消失，所以他回到家以後馬上用電腦打開試算表軟體，先把 N 的更高次方 N⁴, N⁵, …, N^K 全部的值都列出來，拿起計算機一個數字、一個數字地加求取位數根，直到試算表都出現了科學符號還停不下來。

這精神相當可敬但方法太傻了，還記得位數根的第一位快樂夥伴費波那契數列和他的兔子嗎？我們可以使用試算表的公式自動計算位數根，這裡也幫大家建立好了線上表格，點進去先觀察一下再回來讀文章，數學的樂趣源自於觀察。

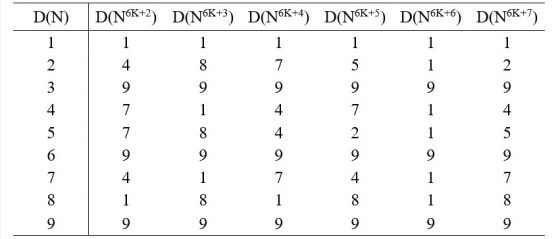
藉由電腦輔助發現的規律如下表，D(N) 表示自然數 N 的位數根，K 表示非負整數，也就是從 0 開始的整數。

表 2：自然數 N 在不同次方數的位數根

為什麼表 2 裡頭 D(N^6K+2) 的 2 次方前面要加一個 6K 呢？首先藉由現代智多星電腦的幫忙，在剛剛的線上表格發現了一件事情，N⁸ 和 N² 的位數根 D(N⁸) 和 D(N²)這兩欄的數字是一樣的，而 N⁹ 和 N³ 的位數根 D(N⁹)和 D(N³)也是一樣的，以此類推，也就是說位數根的次方從 D(N⁸)開始就會重複。

首先，來探討 D(N) = 1 到 9 這九個數字隨著次方增加的變化：

D(N) = 1 那一列的數字都是 1，所以每 1 個次方皆重複一次；

D(N) = 2 那一列的的循環數字是 4,8,7,5,1,2，每 6 個次方重複一次；

…

其他數字以此類推可以產生下面這個表格，描述 D(N)= 1 到 9 時，其次方數的規律是每幾個次方重複一次：

表 3

同樣為了方便討論以及適當地呈現表格，取 6 （也就是 1, 2, 3, 6 的最小公倍數）做為次方數的規律個數。所以在表 2 第一列每一個次方前面要加一個 6K，表示每 6 個次方數一循環。

知道 6K 是怎麼來的以後，緊接著來探討一下是幾個數字一循環。除了 D(N²)那一欄是 9 個數字一循環，D(N⁴)、D(N⁵)、D(N⁷)也同樣是 9 個數字一循環；而 D(N³) 和 D(N⁶) 都是 3 個數字（1, 8, 9 和 1, 1, 9）即重複。同樣為了便於討論，在此使用 9 和 3 的最小公倍數 9，也就是 9 個數字一循環來表示。

為什麼表 2 是從 D(N^6K+2)開始，為什麼不是從 D(N^6K+1) 開始？還有為什麼這個表格沒有出現 3 和 6 這兩個數字？

第一個問題是大家有發現到表 2 的 D(N) 和 D(N^6K+7)的數字組成蠻像的嗎，9 個數字裡面有 7 個數字是一樣的，相似度高達 78 %，只有在 D(N) = 3 和 D(N) = 6 的時候數字不同。3 和 6 的平方都是 9 的倍數，所以 D(N) = 3 和 D(N) = 6 除了本身的一次方之後，平方之後的項都會是 9 的倍數，位數根也必為 9，自然而然在表 2 裡頭除了 D(N) 這一欄之外不會出現 3 和 6 這兩個數字。為了描述的一致性因此自然數 N 在不同次方數的位數根是從 D(N^6K+2)開始。

原本只是一個國中課本必備的通常也沒人去翻閱的乘方開方表，竟然隱含了數字甚至次方的規律，一直到宇宙的盡頭也不會停止。發現數學規律感覺到的快樂，就像是發現控制籃板球的人就能控制整場比賽，那樣使人嘴角上揚。

p.s. 想要嘗試嚴謹證明位數根的加法律、乘法律、指數律的讀者，可以嘗試從這個地方開始思考。對任意自然數 X，X = 9K + D(X)。K 為非負整數，D(X) 為 X 的位數根。

生命靈數能代表宇宙的秩序？

看完上面的故事，覺得那位少年很瘋狂嗎？偷偷告訴你一個祕密，他常常觀察路上的車牌在腦海中自動計算找規律。（那位少年究竟是不是作者本人呢？）

其實他不是特例，因為，人類對數字的狂熱就是沒有極限！狂熱的代表是生命靈數（Numerology）也被稱為數秘學，好人一生會平安或不安的生命歷程都號稱和生命靈數脫不了關係。等等，在數學科普文章裡面介紹謎樣的生命靈數這樣科學嗎！？

回答這問題之前，先告訴你們一件意外的事實，人們從古早時候就開始研究生命靈數並且樂此不疲，而畢達哥拉斯學派是發展最極致的一支，此學派源自希臘哲學家暨數學家畢達哥拉斯，畢氏定理的畢就是這個畢。

生命靈數家堅信每一個數字有自己的個性，可以利用數字更加瞭解自己以及世界，甚至預測未來趨勢。主要論點是人生和宇宙是一個有秩序的系統，而數字反映了其中的秩序，數字 1 至數字 9 各代表了不同的性格原型。因此發展了各種類型的生命靈數，像是以生日的年月日加總後的生命靈數，還有將英文姓名中的字母轉換成數字再進行加總的生命靈數。

相信大家都可以了解最常見的「生命靈數」就是把生日的每一個數字加起來，加到不能夠再加就是生命靈數，用數學的說法就是生日的位數根。例如說泛科學的生日是 2011 年 11 月 4 日，生日位數根是 1。

可是很多人的生日位數根也是 1 耶，這樣可以說他們和泛科學的某些特性是共通的，因此成為泛科學的粉絲嗎？那其他生日位數根的粉絲呢？顯然沒法只用生日位數根解釋。宇宙之中若有規則存在，也必然超越了幾個數字加總後得到新數字代表的狀態。

生命靈數之於數學，就像是占星術之於天文學，以及鍊金術之於化學[1]。所以生命靈數科不科學這件事和研究星座是類似的，大家對自己生命狀態感到不確定或混沌時，會特別容易自我投射到平常未曾留意的敘述之中。

對數字的狂熱，沒有極限

很多數學家、數學愛好者，或者顯然就是作者本人的那位少年，因為沉浸在自己的小世界，而且有時會莫名地嘴角上揚因而被稱為 geek；生命靈數愛好者對於探究命格或規律的興趣濃厚到發展出 Numerlogy 這門學問，並且認為數字能夠代表宇宙的秩序，看起來他們才是對數字最狂熱的一群人吧！

• 此文作者本系列文章獲得臺北市政府文化局藝文補助

參考資料

• 數秘學，維基百科