兔子生兔子，費波那契生出費氏數列——位數根的快樂夥伴（一）

修長的雙耳、無辜的眼神、強勁的後肢、柔順的絨毛、蓬鬆的短尾，以及鼓起的腮幫子…他都沒有。但是止不住的口部運動，仍使他像極了嚼草的兔子。^[1]他不可愛，應該說現在可愛不起來。這不全然基於中年大叔的外型，更因為那藥物副作用所帶來的無奈。

雙極性疾患

還是個 20 歲青春少年兄的時候，他有陣子心情緊張，睡眠需求銳減，出現視聽幻覺以及關係妄想（referential delusions）。^[1]深信一些隨機遇上的事物，跟自己有特定關係。^[2]當時的醫師診斷他處於雙極性疾患（舊稱「躁鬱症」；bipolar disorder）的躁期（manic episode）。從此他屢次住院，接受各式治療。二十年來，總共經歷 8 次躁期；與 2 次狀況相反，情緒低落的鬱期（depressive episodes），更在墜至谷底時試圖自殺。^[1]

40 歲那年，他又陷入躁期：具攻擊性、亢奮少睡、躁動不寧、被害妄想，並且無法控制心中怒火。住進土耳其科尼亞研究暨訓練醫院（Konya Research and Training Hospital）前，他理應每日服用情緒穩定劑lamotrigine和valproic acid，以及抗精神病藥物risperidone。然而最末項，卻被他自行停藥。醫師決定保留前二者，再加上口服的抗精神病藥物aripiprazole，稍後又將其改為同成份的長效型肌肉注射。^[1]

Aripiprazole

Aripiprazole（阿立哌唑；商品名：Abilify、安立復）是第二代抗精神病藥物，主要用於思覺失調症（schizophrenia）與雙極性疾患；也能治療泛自閉症障礙（autistic spectrum disorder）、重度憂鬱症（major depressive disorder）以及妥瑞症（Tourette syndrome）。^{[3, 4]}療效來自對多巴胺和血清素受器的作用，能降低精神科住院機率。比起第一代以及其他第二代的抗精神病藥物，aripiprazole比較不會在運動和代謝方面，造成副作用；^[4]也不容易因為阻斷多巴胺受器，而導致肢體不受控制的錐體外症狀（extrapyramidal symptoms，簡稱EPS）。^{[4, 5]}

在採用肌肉注射前，必須先口服同成份的藥物，建立耐受性（tolerability）。^[4]確保病患於可容忍的副作用範圍內，安全地獲得療效。這對將來長期使用此藥的成功與否至關重要。^[6]從口服轉換至注射的頭14天，仍得持續使用口服藥物。在施打第一劑aripiprazole後，約 5 至 7 日左右，藥物會達到最高血漿濃度。 ^[4]

兔子症候群

打完那劑aripiprazole的一個月後，男子的嘴巴不由自主，又開又閉，速度之快，猶如忙碌進食的兔子。^[1]

兔子症候群（rabbit syndrome）首見於 1972 年，是一種罕見的錐體外症狀。^{[1, 7]}通常是第一代抗精神病藥物所致；不過偶有第二代的案例出現。^{[1, 8]}整體來說，影響約 1.5 至 4.4% 的抗精神病藥物使用者。^[9]病患嘴巴的肌肉會以每秒 4 到 6 次，也就是平均 5 赫茲（Hz）的頻率，規律地垂直運動，神似兔子咀嚼。^{[1, 7, 9, 10]}嘴唇開闔時，多少會發出「啵、啵」聲。^[10]此症不涉及舌頭，^{[8, 10]}亦不妨礙口語溝通，甚至在講話時會暫時消失。（請見下方影片。）^[9]

治療雙極性疾患固然重要，也不能放任惱人的副作用不管。醫師逐漸減少男子 aripiprazole 的劑量，直到完全停用。^[1]同時，開立對付動作障礙疾病的抗膽鹼藥物 biperiden，以及能鎮靜神經的苯二氮平類藥物 diazepam，讓他每日服用。^{[1, 11, 12]}花了二個月的時間，兔子症候群的症狀才完全消失。

參考資料

1. ‘11th International Congress on Psychopharmacology & 7th International Symposium on Child and Adolescent Psychopharmacology’. (2019) Psychiatry and Clinical Psychopharmacology, 29:sup1, 129-263.
2. Startup M, Startup S. (2005) ‘On two kinds of delusion of reference’. Psychiatry Research, 15;137(1-2):87-92.
3. ‘Aripiprazole’. (15 JAN 2022) MedlinePlus.
4. Gettu N, Saadabadi A. (21 MAY 2022) ‘Aripiprazole’. In: StatPearls. Treasure Island (FL): StatPearls Publishing.
5. D’Souza RS, Hooten WM. (01 AUG 2022) ‘Extrapyramidal Symptoms’. In: StatPearls. Treasure Island (FL): StatPearls Publishing.
6. Stanulović V, Hodolic M, Mitsikostas DD, et al. (2022) ‘Drug tolerability: How much ambiguity can be tolerated? A systematic review of the assessment of tolerability in clinical studies’. British Journal of Clinical Pharmacology, 88(2):551-565.
7. Rissardo JP, Caprara ALF. (2020) ‘Cinnarizine- and flunarizine-associated movement disorder: a literature review’. The Egyptian Journal of Neurology, Psychiatry and Neurosurgery, 56, 61.
8. Gundogmus I, Tekin S, Tasdelen Kul A, et al. (2022). ‘Amisulpride-induced late-onset rabbit syndrome: Case report and literature review’. European Psychiatry, 65(S1), S712-S712.
9. Aniello MS, Altomare S, Difazio P, et al. (2021) ‘Functional Rabbit Syndrome: A Case Report’. Tremor and Other Hyperkinetic Movements, 11(1):56.
10. Catena Dell’Osso M, Fagiolini A, Ducci F, et al. (2007) ‘Newer antipsychotics and the rabbit syndrome’. Clinical Practice and Epidemiology in Mental Health, 3, 6.
11. U.S. National Institute of Diabetes and Digestive and Kidney Diseases. (20 JUL 2017) ‘Biperiden’. LiverTox: Clinical and Research Information on Drug-Induced Liver Injury.
12. Dhaliwal JS, Rosani A, Saadabadi A. (03 SEP 2022) ‘Diazepam’. In: StatPearls. Treasure Island (FL): StatPearls Publishing.

本文轉載自諾貝爾化學獎專題系列，原文為《【2011諾貝爾化學獎】具有黃金比例的晶體 — 準晶》

• 譯者／蔡蘊明｜台大化學系名譽教授
• 圖／曹一允｜美國德州農工大學 Karen Wooley 教授指導下取得博士，現於日本萊雅公司進行研究。

十重對稱的黃金比例

當丹尼．謝西曼（Daniel Shechtman）將這個讓他得到 2011 年諾貝爾化學獎的發現登記於實驗記錄簿上時，在後面寫下了三個問號，因為從那些在他眼前的晶體裡面的原子，產生了一個不可能的對稱性，那就好像一個足球——一個球面 ——不可能只由正六邊形組成。從此之後，有趣的馬賽克圖案（Mosaic）、數學裡面的黃金比例以及藝術，幫科學家們解釋了謝西曼那令人困惑的觀察。

「Eyn chaya kazoo」，丹尼．謝西曼用希伯來語告訴自己「不可能有這種東西」。時值 1982 年 4 月 8 號的早晨，他正在研究的物質，是一個由鋁和錳組成的混合物，看起來很奇怪，因此他用電子顯微鏡，企圖從原子的層次來觀察，但是透過電子顯微鏡得到的圖像，卻違反了所有的邏輯：他看到一些同心圓，每一個都是由十個相互等距的亮點所組成（圖 1）。

謝西曼迅速地將灼熱的熔化金屬冷卻下來。這種溫度的突然改變應該會讓原子的排列混亂，但是他所觀察到的圖案，卻說出了一個完全不同的故事：那些原子以一種違反自然定律的方式而排列。謝西曼一再重複地數著那些點，四個或六個點是可能的，但十個是絕不可能。他在實驗記錄簿上寫下：十重對稱？？？

一個未知的發現

為了瞭解謝西曼的實驗結果，以及為何他會如此驚訝，讓我們想像下面的一個課堂實驗：一位物理老師讓光通過一個鑿有縫隙的金屬板，一個被稱為繞射光柵的物體（圖 2），當光波通過這個光柵時，它會產生折射，就好像海浪的波紋通過一個防波堤的開口一般。

在光柵的另一邊，波紋以一個半圓方式散開，並與其它的波紋相交，波峰與波谷相互地加強或減弱。在繞射光柵後面的螢幕上，一種具有明暗的紋路出現，稱為繞射圖紋。

這就是謝西曼在 1982 年 4 月早晨所得到的那種繞射圖紋（圖 1），只不過他的實驗是不同的：他不是用光，而是用電子（註：電子具有波的性質），而他的光柵就是那個快速冷卻了的金屬原子之間的縫隙。

此外，他的實驗是三度空間的，而非平面的。

那個繞射圖紋顯示，在那金屬之內的原子是排列成一個整齊有序的晶體。這當然不意外，幾乎所有的固體物質，不論是冰塊或金子，都具有整齊的晶體。雖然謝西曼使用電子顯微鏡非常有經驗，然而，一個由十個亮點排列成的圓形，卻是過去他從未看到過的。

更有甚者，這樣的晶體並沒有被列在國際晶體規格表之內，那是一個結晶學的主要參考指引。在當時的科學，明訂了一個由十個亮點排列成的圓形圖紋是不可能的，而其證明是非常簡單而明顯的。

違反所有邏輯的圖紋

在一個晶體中，原子是以固定而重複的方式排列的。決定於化學的組成，它們會具有不同的對稱性。在圖 3a 中，我們可以看到每一個原子是由三個原子圍繞著，而形成不斷重複的排列圖案，產生一個三重對稱；將此圖案轉動 120 度，又會得到相同的圖案。

同樣的原理發生在四重對稱（圖 3b）以及六重對稱（圖 3c），圖案不斷重複。當你個別地轉動 90 度或 60 度，相同的圖案會重複出現。

然而，五重對稱（圖 3d）是不可能的，某些原子之間的距離會小於其它原子之間的距離，也就是說，相同的圖案不會重複。科學家認為這足以證明五重對稱不可能存在於晶體中。同樣的原因存在於七重對稱或更高重的對稱。

謝西曼卻發現，他的圖案轉動一個圓的十分之一的角度（36 度）時，又可得到相同的圖案。他的確看到了一個被認為不可能的十重對稱，因此，不意外地，他在實驗記錄簿上寫下了三個問號。

基本假設出錯了

在美國國家標準局（NIST），謝西曼從他的辦公室向外探頭，望了望走廊，希望能看到某一個可以與他分享發現的人，但是走廊空無一人，所以他回到電子顯微鏡前，對那個晶體繼續進一步的實驗。其中他重複地確認所得到的不是巒晶（twin crystal）：兩種共生的晶體享有相同的晶面，而導致了奇怪的繞射圖紋；但是他無法找到任何的跡象顯示那是巒晶。

除此之外，他將電子顯微鏡下的晶體轉動，看看到底要轉多少度可以讓這個十重對稱的繞射圖紋重複出現。實驗顯示晶體的對稱性與圖紋的十重對稱不同，但仍然是一個不可能的五重對稱。謝西曼的結論是：科學界的基本假設是錯誤的。

當謝西曼告訴科學家們他的發現時，他面對了完全的否定，一些同事們甚至認為這根本是無稽之談，許多人宣稱他所得到的是巒晶。實驗室的主管丟給了他一本結晶學教科書，建議他讀讀。謝西曼當然知道教科書裡面說了什麼，但是他更相信自己的實驗。

根據謝西曼的回憶，所有的騷動終於導致他的老闆要求他離開那個研究小組，狀況變得非常難堪。

與已知奮戰

謝西曼是在以色列科技大學（Technion-Israel Institute of Technology）修得博士學位的。在 1983 年，他引發了在他母校任職的伊蘭．布雷契（Ilan Blech）對這個研究的興趣，他們合力企圖解釋此一繞射圖紋，並轉譯成為原子在晶體內的排列模式。

於 1984 年夏，他們送了一份論文稿到應用物理期刊（Journal of Applied Physics），但是該稿似乎在收到當日，就即刻被編輯退回。

接著，謝西曼向約翰．康（John Cahn）提出要求。康是一位著名的物理學家，也是當初邀聘謝西曼到 NIST 的人。謝西曼希望康能看看他的數據。這位通常很忙的學者終於答應，接著，康與一位法國的結晶學家丹尼斯．格拉提亞斯（Denis Gratias）諮詢，看看謝西曼是否忽略了什麼，但是根據格拉提亞斯的檢驗，謝西曼的實驗是可以信賴的，格拉提亞斯如果親自做那些實驗，也會使用同樣的方法。

在 1984 年的十一月，偕同了康、布雷契與格拉提亞斯，謝西曼等人終於在 Physical Review Letters 這份期刊中，共同發表了他的數據。這篇論文像顆炸彈一般，投在結晶學者之間。它質疑了他們的科學學門中的最基本教條：所有的晶體具有重複的週期性結構模式。

揭開知識的迷障

現在這項發現觸及了更多的讀者，而謝西曼成為了更多批評的目標。不過，在此同時，全世界的結晶學者們都產生了一種似曾相識的感覺，許多人在分析一些其它的物質時，也曾經得到過類似的繞射圖紋，但是當初，他們都將之視為巒晶的證據。現在，他們開始翻箱倒櫃，找出以前的實驗記錄簿，很快發現有些其它的晶體也會產生這種看似不可能的圖紋，譬如八重和十二重的對稱。

在謝西曼發表了他的發現之後，他仍然不知道那個奇怪的晶體內部結構到底如何。顯然地，它的對稱性是五重的，那是何種堆疊方式呢？這個答案卻從另一個未曾料到的領域而得：數學中的馬賽克遊戲。

用以解謎的馬賽克

數學家們喜歡用迷團和邏輯問題來挑戰自我。於 1960 年代，他們開始思索是否可以用有限數目的圖案塊，舖出不會重複的馬賽克圖案，創造一種所謂的「非週期馬賽克」。

頭一個成功的嘗試是在 1966 年，由一位美國的數學家所發表，但是他需要超過兩萬種圖案塊來做到，這很難讓著迷於精簡的數學家滿足。當更多的數學家投入這項挑戰，需要的不同圖案塊數目穩定下修。

終於，在 1970 年代中期，一位英國數學教授羅傑．潘洛斯（Roger Penrose）對此問題提出了一個最漂亮的解答。他用僅僅兩種圖案塊創造出非週期馬賽克，例如一胖一瘦的菱形（圖 4-1）。

潘洛斯的馬賽克在好幾個不同方面啟發了學界，其中之一是他的發現被用來分析中世紀伊斯蘭綺理（Girih）圖案。我們也發現阿拉伯藝術家早在 13 世紀就創造出了非週期馬賽克，這種馬賽克裝飾著非凡的西班牙阿罕布拉宮，還有伊朗 Darb-i Imam 寺廟的入口和穹頂。

結晶學者艾倫．馬凱（Alan Mackay）運用潘洛斯的馬賽克於另一個方面，他想探究構成物質的原子是否也能如同非週期馬賽克的圖案般排列。他做了一個實驗，用代表原子的圓圈放置在潘洛斯的馬賽克圖案的交點位置（圖 4-2），然後用這樣的圖案作成繞射光柵，來看會得到何種繞射圖案，結果得到一個十重對稱——十個光點圍成一圈。

馬凱的模型與謝西曼的繞射圖紋之間的關聯性，接著被物理學家保羅．史坦哈特（Paul Steinhardt）與多夫．李凡（Dov Levine）所發現。謝西曼的論文在 Physical Review Letters 這份期刊上發表之前，編輯將該文稿交由其他的科學家審核，在這個過程中，史坦哈特有機會看到這份文章，他早就對馬凱的模型熟悉，因此體認到馬凱的理論模型，存在現實世界中，亦存在於謝西曼在 NIST 的實驗室裡。

在 1984 年的聖誕夜，就在謝西曼的論文出刊後的四週，史坦哈特與李凡發表了一篇論文，其中描述了準晶體（quasicrystal）以及它的非週期馬賽克排列。在這篇論文中，準晶體得到了它的名字。

關鍵的黃金比例

準晶體與非週期馬賽克具有一項共同的迷人特質，那是一個在數學與藝術中不斷出現的黃金比例，亦即數學常數 tau。例如：在潘洛斯的馬賽克中，胖的和瘦的菱形數目的比例是 tau；類似地，準晶體中原子間的不同距離的比例，總是與 tau 相關。

13 世紀的義大利數學家費布那西（Fibonacci），從一個有關兔子繁殖的假設性實驗中找到的一系列數字中，描述了這個數學常數 tau。在這個著名的數列中，每一個數字是前兩個數字之和：1、1、2、3、5、8、13、21、34、55、89、144 等等。如果將一個費氏數列中較大的數字除以前一個數字，例如 144/89，你就會得到一個接近黃金比例的數字。

當科學家想要用一個繞射圖紋來描述準晶體中的原子排列時，費氏數列與黃金比例對他們是很重要的。費氏數列也可以解釋 2011 年的諾貝爾化學獎所表彰的發現，為何改變了化學家對晶體結構的規律性之看法。

不會重複的規律

先前，化學家解釋晶體的規律性在於一個週期性不斷重複的模式。費氏數列雖然不會重複，卻也是規律的，因為它遵守一個數學的規則。

在準晶體中，原子間的距離與費氏數列相關，原子以規律的方式排列，化學家可以預測一個準晶體中的結構是何樣，不過這種規律性與具有周期性結構的晶體是不同的。

在 1992 年，這個認知導致了國際結晶學會改變了他們對晶體的定義。先前對晶體的定義是「一個物質，其中組成的原子、分子或離子以一個整齊而且重複的方式堆疊成立體的型態」，現在新的定義是「任何固體，基本上具有可區別的繞射圖紋」，這個定義比較寬廣，而且允許未來可能發現的其它種晶體。

準晶體也存在於…

從他們 1982 年的發現之後，數以百計的準晶體在全球許多實驗室中被合成，但一直到了 2009 年的夏天，科學家才第一次報導了天然的準晶體。他們發現了一種採自東俄的哈吐卡（Khatyrka）河的樣本中之礦石。這種礦石是由鋁、銅和鐵組成，具有一個十重對稱的繞射圖紋。它被稱為二十面石（icosahedrite），此名源自於二十面體（icosahedron），那是一種具有 20 個正三角形面的幾何固體，黃金比例存在於其幾何結構中。

準晶體也被發現存在於一種世界上最耐用的鐵當中。在嘗試不同組合的金屬時，一家瑞典的公司成功的製備出一種鐵，具有許多令人驚訝的良好特質。分析它的原子排列結構時，顯示它具有兩種相：硬鐵的準晶體嵌在一種較軟的鐵中，此一準晶體具有一種盔甲的功能。現在它被用於刮鬍刀片，以及眼睛手術的細針等產品中。

除了特別堅硬外，準晶體能像玻璃般輕易的碎裂。

由於其特殊原子排列結構，它們也是很差的熱與電的導體，以及含有不具黏性的表面。其低熱傳導的性質可以讓它們成為有用的熱電材料，能將熱轉為電，發展這種材料的目的在解決熱能的再利用，例如用在汽車與卡車上。現在科學家們正在實驗將準晶體用做像是煎鍋，以及節能的發光二極體（LED）之表面塗料，或是作為引擎的隔熱等等。

保持開放的心

謝西曼的故事並非唯一。

在科學的歷史中，一再地有研究工作者被迫與已經建立的「真理」作戰。事後看來，那些真理不過是一些假設。謝西曼和他的準晶體所面對過的最嚴厲批評，來自於鮑林（Linus Pauling），他曾得過兩次諾貝爾獎。這很清楚地顯示，即使是我們最偉大的科學家，也無法免疫於被陷在舊教條當中。

保持一個開放的心態，勇於質疑已經建立的知識，實際上可能是科學家們最重要的性格特質。

參考資料

• 本文譯自諾貝爾化學獎委員會公佈給大眾的新聞稿：http://www.nobelprize.org/nobel_prizes/chemistry/laureates/2011/info_publ_eng_2011.pdf
• 若需要進一步的資訊，請至以下網頁點選：http://www.nobelprize.org/nobel_prizes/chemistry/laureates/2011/sciback_2011.pdf

• 作者：王浤齡、陳玟蓉、高珮珊／台北市立大同高級中學

「數感盃青少年寫作競賽」提供國中、高中職學生在培養數學素養後，一個絕佳的發揮舞台。本競賽鼓勵學生跨領域學習，運用數學知識，培養及展現邏輯思考與文字撰寫的能力，盼提升臺灣青少年科普寫作的風氣以及對數學的興趣。
本文為 2021 數感盃青少年寫作競賽／高中組專題報導類佳作之作品，為盡量完整呈現學生之作品樣貌，本文除首圖及標點符號、錯字之外並未進行其他大幅度編修。

在拍照時，我們總是希望能夠自然地呈現出最漂亮的自己，但這是一件何其困難的事情。法國傳奇攝影師——羅伯特・杜瓦諾曾說：「如果我知道如何拍出好照片，那我每次都會拍出好照片了。」然而有沒有什麼拍攝方法，可以讓照片中的身材比例變得更完美呢？ 

有一天，我和一群朋友到某間知名服飾店逛街，試穿今年流行的秋冬款，並拍照片比較看看，選出較適合自己的衣服。在過程中，我發現一個問題：「為什麼在店家試穿時，全身鏡映照出的自己總是比照片中好看？」

嘗試幾次後，我們發現這是因為自己的身材比例，在鏡子與照片中的呈現是不一樣的，服飾店內的全身鏡，總是使腿的比例看起來比較長。

於是我們開始好奇，拍照時要如何拍攝出如同店裡的全身鏡具有長腿效果的方法，以及，是什麼原因讓這間服飾店內的全身鏡會有這樣長腿的效果呢？ 

上網搜尋之後，發現在這個社群軟體發達的時代，網路上有許多人分享不用俢圖軟體，就能「拍」出完美比例的文章或是教學影片，其結論是：「把手機或相機傾斜一個角度，就可以讓人的腿在照片中的比例變長。」然而，所謂的「傾斜一個角度」到底是幾度，卻沒有網站提供。

事實上，每個人身高比例皆不相同，取景的遠近都不一樣，甚至使用的拍攝器材也不 盡相同，使這個「角度」也會因情況而有所不同。因此，我們試著用所學的數學工具，去推論出不同人在拍照時，手機應該要傾斜幾度才能達到想要的長腿效果？ 

關於服飾店內全身鏡有長腿效果的原因，我在觀察這些鏡子後，發現它們都有傾斜（如圖一），而且與地面都是夾 80 度。這個傾斜角度到底有什麼樣的用意呢？我們試圖去解開這個業界沒有說出來的秘密。 

首先，我們先解釋物理上的「成像原理」。人的眼睛之所以能看到物體、相機可以拍到畫面，都是因為物體反射的光線，進入到眼睛內的視網膜、或是相機裡的底片後所成的「像」。

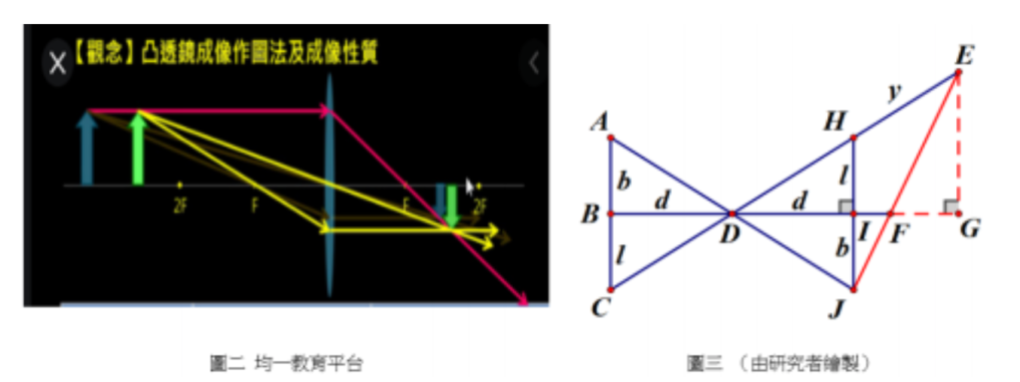
成像的原理與國中理化所教的凸透鏡成像原理相同，是由三條光線所交會而成的像（圖二），其中平行光通過透鏡後會穿過焦點，而穿過焦點的光通過透鏡後會成為平行光，交會處就是成像地點；並且第三條穿過透鏡的直線光也會與前兩條相交，因此可以由物距與像距算出成像縮放的倍率。 

如果我們在成像位置放一個平面，當成像的平面與物體是平行時，像會與實物相似，但是上下顛倒；但是如果把成像平面傾斜一個角度的話，成像的比例就會因為傾斜的角度，而 與實物的原比例不同。 

我們想要研究相機傾斜角度對照片中人物的身材比例的影響。 

考慮拍攝時，相機高度與被拍攝者的肚臍位置相同，如上面圖三所示，點 D 為相機的焦點，物體反射的光線直線穿過 D點，在另一側的平面上呈現一個倒立的像。

把 \( \overline{AC} \) 當成為一位站立著的被拍攝者， \( \overline{AB} \) =b 為被拍攝者的頭頂到肚臍的長度，即為身長；而 \( \overline{BC} \) =l 為被拍攝者的肚臍到腳底的長度，即為腿長； \( \overline{BD} \) =d 為被拍攝者與相機的距離。

當成像平面垂直地面時，若把像距等比例放大到等於物距時（即是 \( \overline{DI} \) =d ），則 \( \overline{HJ} \) 會是一個全等的倒立像，即 \( \overline{HI} \) =l 為像的腿長、 \( \overline{IJ} \) =b 為像的身長。

若把成像平面傾斜一個角度，轉成 \( \overline{EJ} \) ， 則像的身長會被拉成 \( \overline{IJ} \) → \( \overline{FJ} \)  ，像的腿長會被拉成 \( \overline{IH} \) → \( \overline{FE} \) 。

接下來，我們將推導出一條公式，可以算出相機該傾斜幾度，才能讓被拍攝者的身長及腿長呈現我們所想要的比例。 

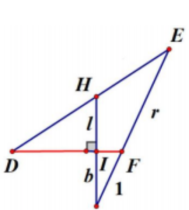
假設在照片中，身長比腿長的比例為 \( \overline{FJ} \) : \( \overline{EF} \) =1 : r，先求出 \( \overline{HD} \) : \( \overline{HE} \) 。

如圖四，我們利用「孟氏定理」， ΔJEH 被直線 \( \overline{FD} \) 所截的線段比為

 \( \frac{\overline{JI}}{\overline{IH}} \) ✕ \( \frac{\overline{HD}}{\overline{DE}} \) ✕ \( \frac{\overline{EF}}{\overline{FJ}} \) =1  \( \Rightarrow \) \( \frac{b}{l} \) ✕ \( \frac{\overline{HD}}{\overline{DE}} \) ✕ \( \frac{r}{1} \) =1，則 \( \frac{\overline{HD}}{\overline{DE}} \) = \( \frac{l}{br} \) 。

又因為圖三中， \( \overline{IH} \) // \( \overline{EG} \) ，所以 \( \frac{l}{br} \) = \( \frac{\overline{HD}}{\overline{DE}} \) =  \( \frac{\overline{DI}}{\overline{DG}} \) = \( \frac{d}{\overline{DG}} \)  \( \Rightarrow \)  \( \overline{DG} \) = \( \frac{bdr}{l} \)

\( \overline{IG} \) = \( \overline{DG} \) – \( \overline{DI} \) = \( \frac{bdr}{l} \) -d

因為 ΔEFG ≈ ΔJFI，所以  \( \frac{\overline{IF}}{\overline{FG}} \) =  \( \frac{\overline{FJ}}{\overline{EF}} \) =  \( \frac{1}{r} \) ；可推得：

\( \overline{IF} \) = \( \frac{1}{(1+r)} \) ✕ \( \overline{IG} \) = \( \frac{1}{(1+r)} \) ✕  \( \left ( \frac{bdr}{l}-d \right ) \)

因此，若相機傾斜的斜率為 m，則

從這個公式可知，我們只要知道以下數據，代入公式之中即可算出相機的斜率：

若圖中 \( \overline{AJ} \) 的斜率與 \( \overline{CH} \) （原文使用的是雙箭頭線段符號，但公式表中找不到，所以就先以線段符號代替）的斜率分別令成 m_b 與 m_l ，則相機傾斜的斜率公式可用斜率簡化表示為

我們根據此公式進行以下實作。 

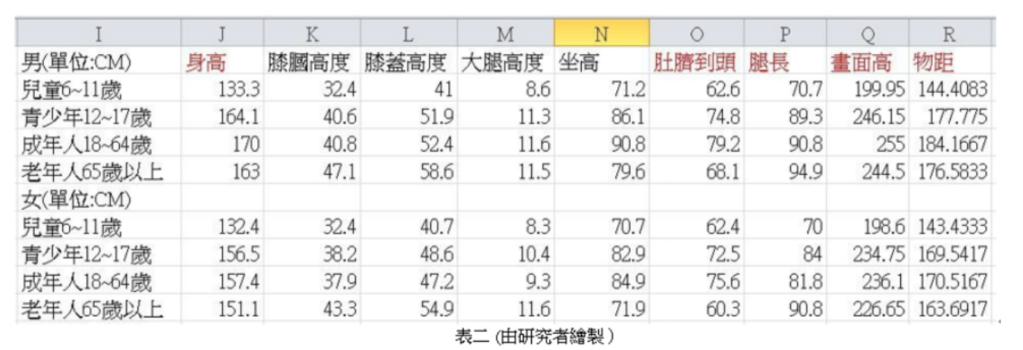
拍攝工具為 iPhone 手機，被拍攝同學的身體數據如下表一： 

我們設定畫面高度與人物身高的比例黃金比例（約為 1：0.618），而由〈物距計算器〉網站，可算出此畫面下的拍攝距離為 144.7 公分。並且，我們希望拍攝出的身長與腿長也是黃金比 例，即  \( r=\frac{1}{0.618}=1.618 \)。

由表一，因為 m_b = －身高 / 物距 =  \( \frac{-67.5}{144.7} \)，m_l = 腿長 / 物距 =  \( \frac{95.5}{144.7} \)，所以帶入公式可得：

因此，拍攝時手機傾斜的斜率約為 8.538，換算成角度： 

所以手機在拍攝這位同學時應該要傾斜 83.3°。

下圖是手機傾斜前後拍照出來的照片效果對比： 

從右圖看得出來，照片中的腿部確實有拉長的效果，其比例為 1 : 1.84，但並非是當初我們給 定的黃金比例。這個原因是來自於 iPhone 手機鏡頭視角的限制，當手機傾斜時，放在腰部的高度，被拍者會無法全身入鏡。所以，我們將手機高度降低至能夠完全拍攝到整個人，因而導致加大拉長效果。

因此，我們建議在拍攝時，若需要降低手機高度，則手機與地面夾角，要比原計算出來的角度更接近 90° 一點。 

接下來，我們利用研究的結果去計算，各個年齡層與性別的人在拍照時，身長與腿長在照片中要呈現黃金比例，手機適當的傾斜角度分別為幾度。

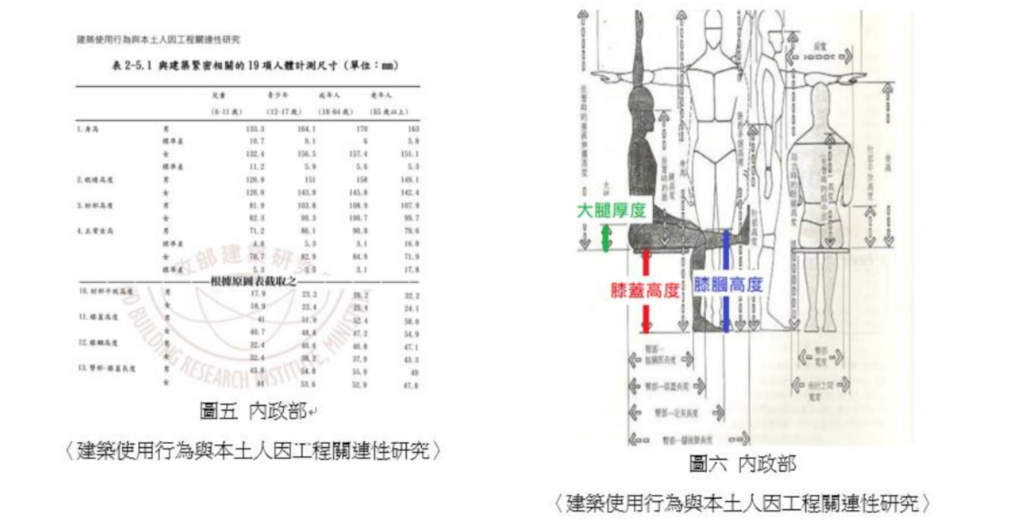
下圖五，是內政部〈建築使用行為與本土人因工程關連性研究〉指出的 19 項人體計測尺寸中的部份數據；而下圖六，則是將圖表的數據進行以下的計算，去推論一般人平均的身長與腿長。

• 膝蓋高度 − 膝膕高度 = 大腿厚度 
• 坐高 − 大腿厚度 = 身長（頭頂到肚臍） 
• 身高 − 身長 = 腿長 

把各個年齡層與性別的平均身長與腿長整理成下表二。最後，我們各別將數據代入公式計算得出，不同人在拍照時，手機的傾斜角度，如下表三所示。 

表格三中，65 歲以上的民眾要拍出黃金比例的手機角度比較垂直，是因為數據的統計有將駝背也考慮進去，導致統計出的結果，相對其它年齡層來說腿的比例較長。但普遍來說， 在未滿 65 歲的各個年齡層拍照時，手機傾斜角度分布在 65 ~ 70° 之間。

然而，考慮到手機傾斜時又要全身入鏡，需要降低手機拍攝的高度，會更加拉大腿長的比例，因此，一般人在拍照時，若想讓身長比腿長接近黃金比例的話，我們建議：

服飾業內不能說的秘密，全身鏡傾斜 80° 的原因！

在前文中，我們想探討第二個問題，是服飾店的全身鏡為什麼都與地面夾 80°。其斜置的原因，明顯是要讓腿看起比較長，但為何不用其它的角度而恰好是 80° 呢？ 

斜鏡面會產生仰視效果，讓人感覺鏡中的人像向後仰，使腿的視覺效果變長。事實上， 長腿效果與我們研究的主題一致，同樣是實物（鏡中後仰的人像）與成像平面（視網膜）不平行，因此後仰角度與視覺比例的關係，符合前文推論的公式。

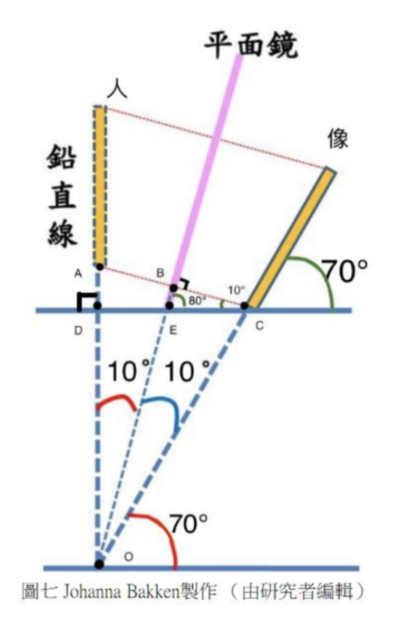
如下圖七所示，全身鏡傾斜 80° 後，由於鏡子和直立的人夾角 O 為 10°，因為鏡射原理，鏡子和像的夾角也為為10°， 所以像會傾斜 70°，且 ∠ACD = ∠AOB = 10° 。

實際到店家測量全身鏡前的走道寬度，約為 78 公分。也就是一般民眾會站在距離約 78 公分的位置使用全身鏡，即 \( \overline{DE} \) = 78，則 

78+ \( \overline{EC} \) = \( \overline{DC} \) = \( \overline{AC} \) cos(10º)

 \( \Rightarrow \) 78+ \( \overline{EC} \) = 2 \( \overline{BC} \) cos(10º)

 \( \Rightarrow \) 78+ \( \overline{EC} \) = 2 \( \overline{EC} \) cos(10º)

因此，可以算出 \( \overline{EC}=\frac{78}{2cos^{2}(10^{\circ})-1}\approx 83 \)

所以當我們照鏡子時，眼睛與成像的距離為 78+83=161 公分。若成年女性（平均身長 75.6 公分、 腿長 81.8 公分）使用服飾店的全身鏡時，看到鏡中自己的比例（腿長 / 身長）為 r，則

 \( \frac{(1+r)\times \left ( -\frac{75.6}{161} \right )\times \left ( \frac{81.8}{161} \right )}{r\times \left ( -\frac{75.6}{161} \right )+\left ( \frac{81.8}{161} \right )}=tan(70^{\circ})\approx 2.747 \)

 \( \Rightarrow \) r ✕ [(-0.4696) ✕ 0.5081+2.747 ✕ 0.4696] = 0.4696 ✕ 0.5081 + 2.747 ✕ 0.5081

 \( \Rightarrow r=\frac{0.4696\times 0.5081 + 2.747\times 0.5081}{ [(-0.4696)\times 0.5081+2.747\times 0.4696] }=\frac{1.63435446}{1.0.5138744}\approx 1.565 \)

這個結果非常接近黃金比例。

用其它年齡層與性別的數據去計算，也可得到 r ≈ 1.618 ± 0.05

因此，我們發現服飾店會在店內全身鏡會斜置 80° 的原因，很可能是因為要讓顧客認為穿上自家的衣服後，會讓比例接近於黃金比例，以提升購買慾望。

結合我們計算的數據和實作的結果，可以得出一些結論：大多數的人拍攝時，如果想要拍出身體的比例接近黃金比例，手機需要傾斜的角度大約為 65° ~ 70°。若將傾斜時，可能會把手機高度降低的因素考慮進去，則是以 70° 為最佳角度。

下次拍照時，不妨也將手機傾斜成 70°，或許會有意想不到的效果！

參考資料

• 均一教育平台
• 內政部建築研究所研究報告
• 物距計算機