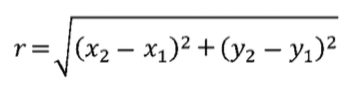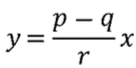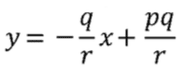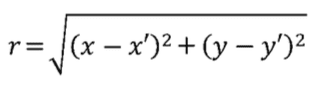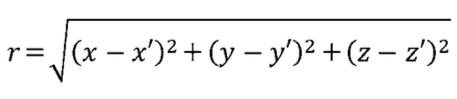劃時代的想法「笛卡兒座標系」
15 世紀,古騰堡(Gutenberg)將活字印刷應用化之後,歐幾里德的《幾何原本》也變成活字版本了。從 1482 年威尼斯的初版開始, 世界上有超過一千種版本,可以說是除了《聖經》之外,銷量最多的 一本書。幾乎可以說《聖經》跟《幾何原本》是支撐歐洲文明的兩大支柱。

為歐幾里德的平面幾何帶來偉大變革的,是 1596 年出生的近代理性主義之父笛卡兒(Descartes)。笛卡兒在他的著作《談談方法》 中,提出追求真理的四大步驟:
1. 如果不是具有明證的真理,就不承認其為真。
2. 為了更加了解問題,要將問題分割成許多小問題。
3. 思考的順序是從單純的事物開始,依序往複雜的事物前進。
4. 小問題都解決了之後,將小問題全部列出來,看看是否有遺漏, 能不能涵蓋原本的大問題。

這也反應出了《幾何原本》的精神,從看起來理所當然的公理開始,一步步推導向複雜的圖形性質。
這個《談談方法》,是討論關於探討真理的方法的書籍序論。笛卡兒提出了一個幾何學上的新見解,做為這個方法的試論,那就是:
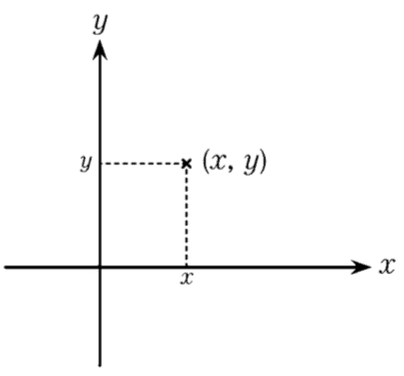
「平面上的點都可以用一組兩個的實數來表示,也就是(x, y)」。
在平面上垂直相交的兩條線,分別稱為 x 軸以及 y 軸。為了表示平面上的點的位置,將點分別與 x 軸以及 y 軸做垂線,相交的點分別為 x 以及 y,於是這個點的位置就可以用 (x, y) 來表 示,這就是所謂的「笛卡兒座標系」(圖 6-10)。
雖然座標軸這個概念並不是笛卡兒發明的, 這樣的座標系也可以稱為「直角座標系」,但因為笛卡兒用這個座標系導入新的幾何學概念,所以我在此稱之為「笛卡兒座標系」。使用笛卡兒座標系的話,平面幾何的問題都可以代換成關於(x, y)的計算問題,連歐幾里德的五個公理, 都可以用笛卡兒座標來解釋了。
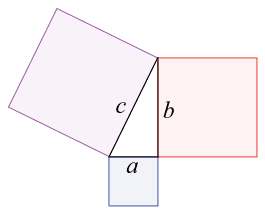
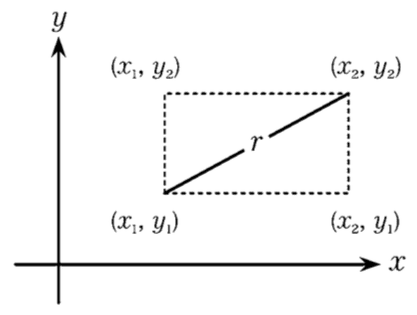
例如,〈公理 3〉提到,平面上兩點(x1, y1)與 (x2, y2),以一點為圓心,求通過另外一點的圓的解。「圓」就是與某一點距離相同的 所有點的集合,所以首先計算這兩點的距離。 如圖 6-11,可以將(x1, y1)與 (x2, y2)的距離,也就是這兩點所連 結的線段想像成長方形的對角線。
根據畢氏定理,對角線的長度 r 的平方,就是長邊與短邊的平方和。也可以表示成:
〈公理 3〉的「以(x1, y1)為中心,通過(x2, y2)的圓」就是與點(x1, y1)距離 r 的所有點的集合,因此滿足下面算式的所有(x, y)的集合就是解答。
(x - x1) 2 + (y - y1) 2 = r2
利用笛卡兒座標系,就可以將歐幾里德的幾何學問題化為方程式問題了。
用方程式解開美妙的「垂心定理」
2009 年,日本數學書房出版了一本名為《這個定理真美妙》(この定理が美しい)的書。這是一個大型企畫,由 20 位作者分別選出自己認為最美妙的數學定理,並且講述定理獨特的魅力,而我也選了「基本粒子論」中使用到的定理。在這本書中,京都產業大學的牛瀧文宏先生選了平面幾何的「垂心定理」。
要介紹垂心定理,得先介紹三角形的垂線。由三角形的頂點向對邊做一條垂直的線,這條線就稱為垂線。三角形有三個頂點,理所當然就有三條垂線。所謂的「垂心定理」是指,這三條垂線必會相交在一個點,而這個點稱為垂心。
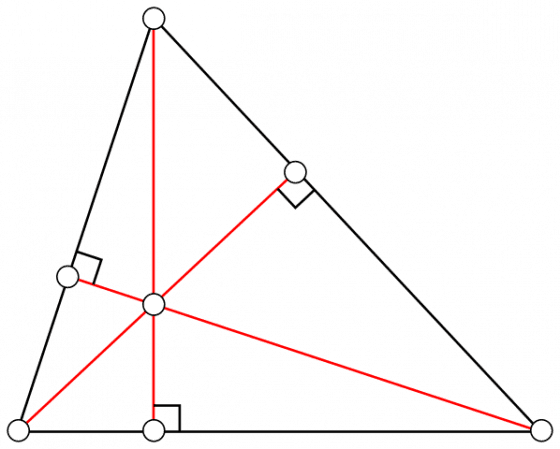
兩條直線如果不是平行的話,一定會在某處相交,形成一個交點,這是理所當然的事情。但是三條直線,就不一定會相交在同一個點了。牛瀧先生在關於垂心定理的描述中提到,「當時身為中學生的我,被那個即使用盡了我的全力也無法到達的境界的證明所懾服,圖形的協調以及層層堆積的理論,使我確確實實感受到定理的美妙」。 古希臘時代流傳下來的,關於垂心定理的證明,巧妙的使用了輔助線,說是藝術也不為過。網路上有許多關於垂心定理的證明,有興趣的人不妨參考。
在這邊利用笛卡兒座標系來證明這個定理。證明中不講求細節, 只是希望大家能感受一下方程式的氣氛,體會一下「將幾何問題化成方程式」的感覺。
假設三角形的頂點為 a = (0,0),b = (p,0), c = (q,r)。頂點 c 對 ab 邊的垂線,可以用方程式表示為:
x = q
頂點 a 對 bc 邊的垂線也可以用方程式表示為:
頂點 b 對 ca 邊的垂線也可以用方程式表示為:
最初的兩個方程式是 x,y 的聯立方程式,求解之後可以得到 :
(x, y) =(q, (p - q)q/r)
這個解也能滿足第三個方程式。也就是說,這三個方程式有共同的一個解。換句話說,三條垂線具有一個共同的交點,也就是垂心。
這個證明不像古希臘流傳下來使用輔助線的證明方法那樣帶有藝術性。只是先將題目中的垂線利用笛卡兒座標表示成方程式,接著解聯立方程式,按照步驟機械式地一步步操作而已。但正是因為不需要靈感,所以只要知道解法,誰都可以證明出同樣的答案。
如果使用輔助線的證明方法是在田野間悠閒騎著腳踏車,享受著田園風景前進,那麼利用笛卡兒座標系的證明方法就如同搭上由精密機械組裝而成的新幹線呼嘯而過一般。笛卡兒座標終結了幾何學的牧歌時代,進入了重視效率的近代。
有科學技術的地方,就有笛卡兒座標系
高斯定理:「如果圖形的邊長比,能夠利用加減乘除或是平方根的有限次數組合來表示的話,這個圖形就可以作圖,如果不能,圖形就不能作圖」也可以用笛卡兒座標系簡單解釋。作圖的基本規則是只使用尺跟圓規,所以又稱為尺規作圖。在笛卡兒座標系中,利用尺畫出的直線,可以表示為一次函數 y = ax + b,利用圓規畫出的圓是二次函數 (x - x1) 2 + (y - y1) 2 = r2 。
因此,重複這些步驟作圖得到的線段長的比值,就是一次方程式以及二次方程式相互組合的解,也就是「可以利用加減乘除或是平方根的有限次數組合來表示」。
笛卡兒座標不僅僅影響了幾何學,對於科學技術方面的影響更是廣泛且重大。笛卡兒出版《談談方法》的序文〈探討真理的方法〉時,剛好是伽利略的晚年。
伽利略發現了許多關於物質運動的重要現象,包括——
- 「鐘擺的等時性」:鐘擺的擺動週期是固定的,與擺動幅度無關;
- 「自由落體法則」:物體落下時所需要的時間與物體重量無關;
- 「慣性法則」:以等速度移動的物體,在不施加外力的狀況下,會一直維持等速度運動;
- 「相對性」:在等速度移動的座標系中的力學法則,看起來與靜止座標系中的力學法則相同。
但是,即使發現了這麼多重大的發現,伽利略卻沒有完成力學體系,其中一個原因,或許是因為伽利略並不知道笛卡兒座標系吧。

在伽利略過世那年出生的牛頓,為了將力學以及重力學的法則用 數學方法表示時所使用的,正好就是笛卡兒座標系。從此以後,科學以及工程學的各式各樣方程式都可以利用笛卡兒座標系表示。
今日,只要是有科學技術的地方,就有笛卡兒座標系。例如,電腦螢幕或是手機畫面上的點的位置,就是轉換成笛卡兒座標系,以數字表示,而能使電腦處理畫面上的圖像。
將思考推往高維度的世界
笛卡兒座標還有另一個重大貢獻,它將人類的思考從平面中解放,前往更高維度。
二維平面的點可以用一組兩個的數字(x,y)表示,三維空間的點也能用一組三個的數字(x,y,z)代表。在三維空間中畫出互相垂直相 交的三條直線,稱之為 x 軸、y 軸、z 軸,在三維空間的點,分別對 這三個軸做垂線,得到 x、y、z 的數值,這個一組三個的數值就是點的座標。
二維平面上兩點(x,y)與(x’,y’)的距離 r 的公式是:
同樣的,三維空間中兩點(x,y,z)與(x’,y’,z’)的距離 r 公式是:
利用座標表示點的位置的話,能夠簡單地表示比三維更高維度的空間。n 維度的空間,就是無數個由一組 n 個數的座標(x1,……,xn)所表示的點的集合。三維的世界是眼睛可以看到的世界,但我們還是會懷疑、思考看不到的四維以上的空間到底有沒有意義。然而,我們的日常生活所遭遇的事物之中,就隱藏著高維度世界。
本文選自《用數學的語言看世界:一位博士爸爸送給女兒的數學之書,發現數學真正的趣味、價值與美》,臉譜出版。