李武炎/曾任教淡江大學數學系,現為《科學月刊》編輯委員
就在幾個月前,今年5月23日,「賽局論」(game theory)大師、也是諾貝爾經濟學獎得主的美國數學家約翰納許與妻子艾莉西亞(Alicia Esther Nash)在美國因車禍雙雙喪命,事實上,納許5月19日剛在挪威奧斯陸領取2015年「阿貝爾獎」(Abel Prize), 他們出席相關活動後,返家途中搭乘了一輛計程車,不幸在新澤西州的快速道路上發生車禍,消息傳來,令人不勝唏噓。
約翰納許(John Forbes Nash Jr., 1928~2015)
「某個程度上,正常思考就是一種對現狀的順從。人們總是想傳達患有精神疾病者煎熬受苦的意象,但其實並沒有那麼單純,我認為精神疾病或瘋狂也可以是一種超脫。」

納許的人生故事,尤其是長期掙扎於精神分裂的情節,曾在2001年被改編拍成電影《美麗境界》(A Beautiful Mind)轟動一時,更奪下2002年奧斯卡最佳影片,在片中飾演納許的影星羅素 克洛(Russell Crowe)傳神的演技,更是令人印象深刻,真實的人生中,納許在1959年因「思覺失調症」入院接受治療,直到1970 年方才出院。
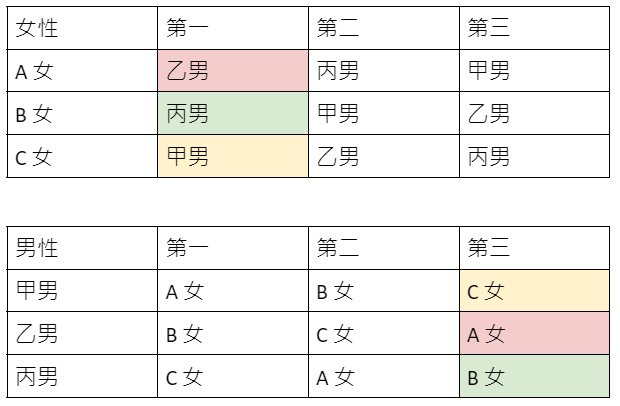
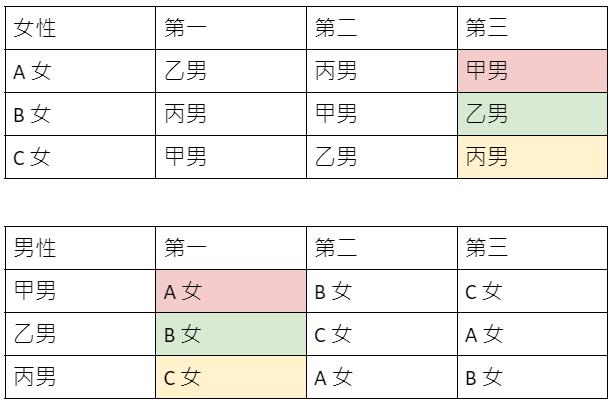
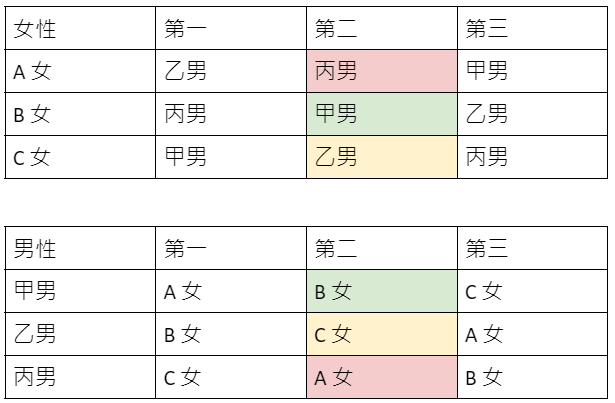
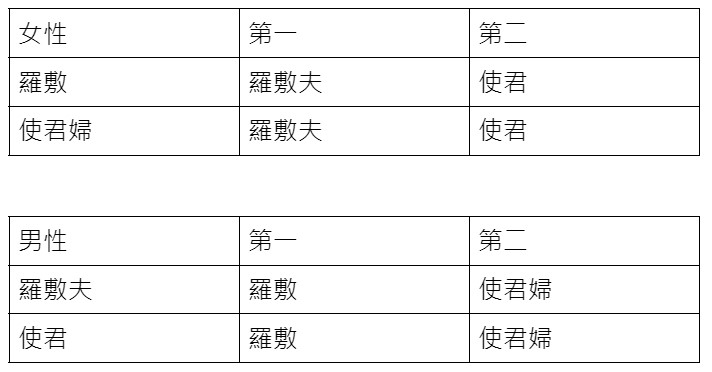
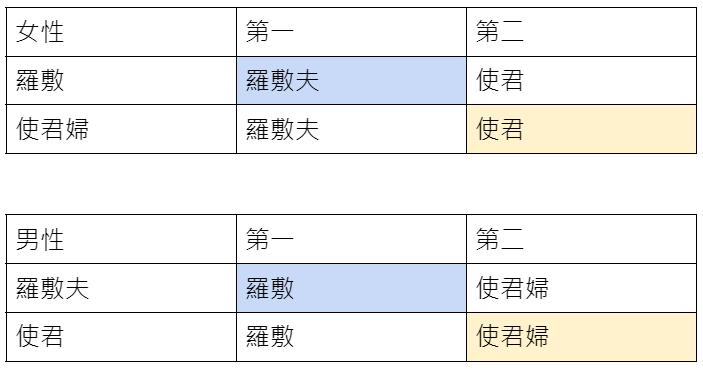
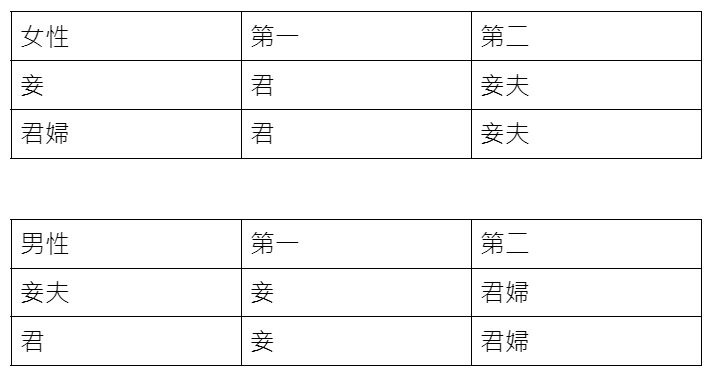
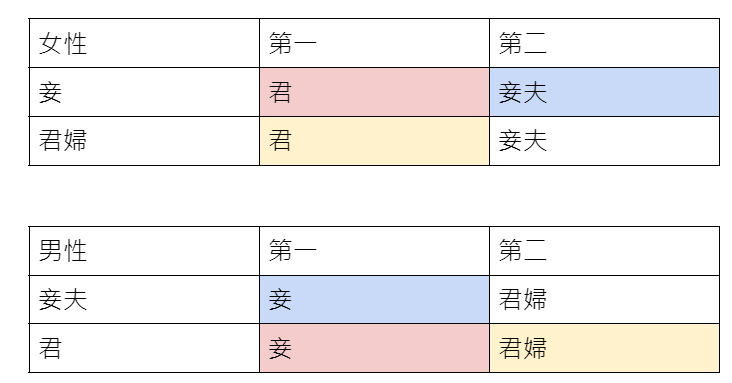
納許本身是一位數學家,他在上個世紀五零年代就已經在數學的研究上作出很多重要的成果,只是外界比較熟悉的反而是他在「賽局論」上的成就,「賽局論」是一個與作決策有關的數學,它最早被應用在經濟學上,變成研究經濟學不可或缺的工具,如今「賽局論」也被廣泛應用於生物學、政治學及控制理論等等的領域。「賽局論」是研究理性決策者之間的衝突與合作所產生的效益的一種數學模式,例子很多,例如打牌、球賽、商務談判等。「賽局論」最有名的問題便是「囚犯困境」的經典例子:
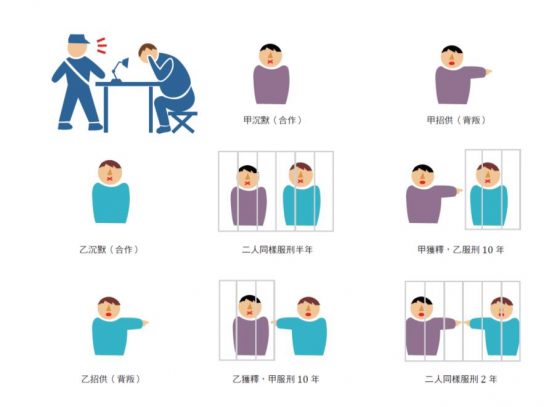
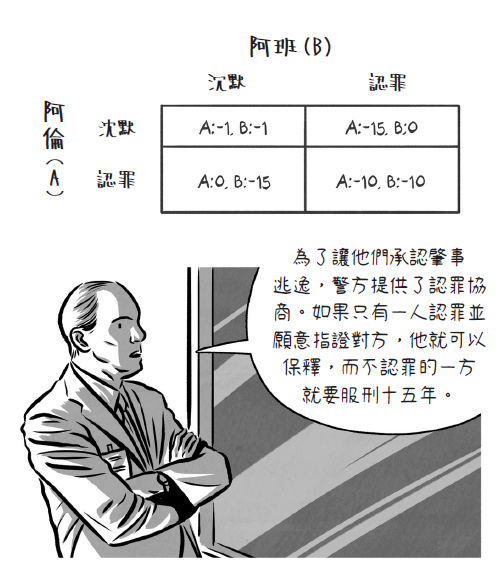
警方逮捕甲乙兩名嫌犯,但沒有足夠證據指控兩人有罪,於是警方將嫌疑犯分開隔離囚禁,而且分別向兩人遊說認罪並提供以下的選擇:
(一)若一人認罪並作證指控對方,而對方不招供,則此人將立即獲得釋放,而被指控者將被判刑10年。
(二)若兩人都不招供,則兩人將同樣被判刑半年。
(三)若兩人都認罪並互相檢舉對方,則兩人將同樣被判2年。
囚犯應該選擇那一種策略才對自己最有利?由於兩名囚犯是被隔離監禁,所以不知對方會選擇哪種策略,試想有理性的囚犯會作出何種選擇,若對方沉默,我指控對方,則我將獲釋,所以我會選擇指控對方;若對方指控我,我如果沉默,則我會被判刑10年,所以我也要指控對方才能獲得2 年較短的刑期。因此我總是要採取指控對方的策略,結果理性的兩人都選擇相同的策略,也就是指控對方,其結果是兩人皆獲判監2年,這在「賽局論」中就是所謂的「納許均衡」(Nash equilibrium)。這也是納許在1950年獲得美國普林斯頓大學數學博士的論文中一個重要的概念,由於他的研究應用在經濟學上的貢獻,使得他與另外兩位「賽局論」的學者約翰海薩尼(John Harsanyi)與萊因哈德謝爾騰(Reinhard Selten)共同獲頒1994年諾貝爾經濟學獎。
納許雖然榮獲諾貝爾經濟學獎,但他本來就是數學專業,他在數學上的研究當然也是非常的傑出,尤其是在廿世紀五零年代,他就已經在數學領域的分支「偏微分方程式」證出很多重要的定理,只是外界比較熟悉的是他在「賽局論」上的成就。由於他在數學上的傑出研究,終於獲得挪威科學與人文研究院的青睞,決定頒授2015年的阿貝爾獎給他,與他同時獲獎的是另外一位美國「偏微分方程式」的巨擘尼倫伯格(Louis Nirenberg),尼倫伯格也是中研院院士林長壽的指導教授。
數學界最崇高的阿貝爾獎
阿貝爾獎常被稱為數學的諾貝爾獎,因為諾貝爾獎項並沒有數學,所以阿貝爾獎可說是數學界最崇高的獎項,它不像另外一個也是數學的菲爾茲獎(Fields metal)有年齡的限制,而且是早年為了彌補諾貝爾獎沒設數學項目的缺憾所提議設立的,不過這個獎項的設立直到公元2002年方才實現,挪威政府為了紀念十九世紀挪威的一位數學家阿貝爾(Niels Henrik Abel,1802~1829)200 歲誕辰,決定設立阿貝爾獎,並且在2003 年開始頒發第一次的獎,獎勵當代研究傑出的數學學者,獎金有挪威幣六百萬克朗(約合750000 美金),歷屆的得主都是當代數學界的翹楚。
阿貝爾是挪威歷史上一位才華橫溢的數學家,他在很年輕時就已經作出很出色的研究成果,其中最有名的是證明一般五次方程式沒有根式解,開啟抽象代數學之濫觴,對代數學往後的發展奠定不可磨滅的根基,他與同時代的法國數學家伽羅瓦(Galois)雙雙被推崇為「現代群論的先驅」。抽象代數中有一種代數結構是運算可交換的「群」,為了紀念阿貝爾,數學圈中就把交換群叫做「阿貝爾群」,英文是「abelian group」,以人命名的專有名詞,在英文的習慣中,第一個字母應為大寫,可是abelian的第一個字母a 卻是小寫,這是因為數學界為了表彰阿貝爾特別卓越的貢獻而把它普通化了,所以如果你在其他地方也看到小寫的專有人名名詞,應該肅然起敬,只有特別了不起的人物才能擁有如此的待遇。
納許與尼倫伯格成為2015 年的阿貝爾桂冠的得主,是因為要表彰他們在數學領域的非線性偏微分方程式及其在幾何分析上的應用,作出顯著與影響深遠的貢獻。偏微分方程式(partial differential equations)是數學的其中一門分支,高中生在高中數學中都學過一點微積分,所涉及的微分都是求單變數函數的導數,而在大學微積分中就會學到多變數函數的導數,針對不同的變數所求的導數就稱為偏導數;因為導數是研究變化率的問題,所以數學中的很多問題以及物理現象,常用與偏導數有關的方程式來描述,因此研究偏微分方程式就成為近代數學的主流,如果方程式中與偏導數有關的項其次數都不超過一次,則這種偏微分方程式就稱為線性(linear),否則就是非線性。非線性方程式(nonlinear partial differential equations)的解法並無一般常規方法可循,幾乎每一種形式都有其特別的解法,而且要用到「分析」的背景知識,分析是指以微積分、無窮級數與解析函數為理論的數學內容,是純數學的三大分支之一,其他兩支為代數與幾何,所以偏微分方程式的題目都很難,為破解非線性偏微分方程的問題,就必須具有獨特與高超的手腕,納許與尼倫伯格就是箇中高手,納許尤其聰明,他的很多這方面的研究都是單打獨鬥自己發明的。
微分流形
除了非線性偏微分方程,納許也專研微分幾何,微分幾何(differential geometry)也是數學的一個分支,主要是研究「微分流形」。流形(manifold)是高等數學中的一個專有名詞,它是一個具有拓樸結構的幾何形體,它的局部具有歐幾里得空間的性質,用比較白話來說,就是近看起來像歐幾里得空間。例如像地球的表面(球面)就是一個流形,我們所處的這個地面範圍看起來是平坦的,這是因為我們所看到的地面其實是地球表面很微小的一部分,所以我們將地面視為平面,但就整個球面而言,它不是平面,我們可以把地球的表面看成一片一片的平面拼接起來,所以球面就是流形的一個例子。當然,流形還是很抽象的概念,簡單地說,它就是高維度的曲線或曲面,物理學中的許多構造也是流形的例子,如力學中的相空間以及廣義相對論中時空模型的「黎曼流形」。
流形中最常應用的是微分流形,它可以用微積分來處理方向、切空間、曲度等問題,而且也用偏微分方程來描述,所以微分幾何與偏微分方程式關係是非常密切的。納許研究微分幾何也會用偏微分方程式作為工具,例如「納許嵌入定理」(Nash embedding theorem):任何抽象的黎曼流形可以嵌入一個歐幾里得空間而保持距離不變;嵌入的意思是把流形放進歐幾里得空間之中而視為一個子流形。為了證明微分幾何中的定理,他必須處理一些特殊偏微分方程式的問題,而這些方程式在以前被公認是不可能解出的,可是納許運用一個迭次的技巧方才克服,這種重複的方法是以確定的部分作為起始點,循序漸進推演,最後求得答案,微積分中的「牛頓法」就是其中一個例子,納許研究的功力真的是一流的,能得到阿貝爾獎真正是實至名歸當之無愧。也是阿貝爾獎得主的葛洛莫夫(Mikhail Gromov)就曾讚許說:「納許在幾何上的貢獻,在我看來,是比他在經濟學上的研究更具無與倫比的偉大,他讓人對流形的看法有不可思議的改變,他能將流形掌握在手,而且比傳統方法更加運用自如。」納許就是玩流形的高手。
令人緬懷的傳奇伴侶
納許早年深受精神疾病所若,沉潛數十年之久,但他後來逐漸復原,重回學術領域繼續研究,他的成就自屬拔尖,他的人生故事就是一段傳奇。對於他的驟逝,數學界為之不捨,也讓世間響起一陣陣嘆惜,納許過世前是美國普林斯頓大學數學系的資深研究員,對於納許的不幸過世,普林斯頓大學群體深感震驚與悲傷,普大校長艾斯格魯伯(Christopher Eisgruber)發表下面的談話:「約翰的卓越成就,激發了數代的數學家、經濟學家與科學家,因為他們都深受納許在賽局論上的顯赫突破所影響,他與夫人艾莉西亞的故事更是感動數以百萬計的讀者與電影觀賞者,他們尤其激賞他倆在面對令人恐懼的挑戰時所展現的無比勇氣。」電影《美麗境界》中飾演納許的羅素.克洛在推特上懷念納許,他寫道:「我心歸之;一對令人神奇的伴侶,美麗的心智,美麗的心靈。」
延伸閱讀:
罹患精神疾病的天才數學家-奈許的美麗境界
數學的諾貝爾獎
什麼?!你還不知道《科學月刊》,我們46歲囉!
入不惑之年還是可以當個科青