- 作者/李奕萱
阿貝爾獎(Abel Prize)自2003年開始由挪威國王頒發給傑出數學家的獎項。阿貝爾獎的歷史可以追溯到1899年,當時挪威數學家索菲斯·李(Sophus Lie)得知阿佛烈·諾貝爾(Alfred Nobel)計劃設立的諾貝爾獎將不包括數學獎,又剛好正逢數學家尼爾斯·亨里克·阿貝爾(Niels Henrik Abel)誕辰100週年紀念,便提出設立阿貝爾獎。 不幸的是,索菲斯·李不久後逝世、提供資金的奧斯卡二世國王也因為瑞典和挪威聯合王國解散而下台,阿貝爾獎這件事也就不了了之。
2001年,人們覺得應該給數學家一個相當於諾貝爾獎的獎項,便再次將阿貝爾獎提案給挪威總理。隔年挪威政府便宣佈撥款2億挪威克朗在數學家阿貝爾誕辰200週年時正式設立阿貝爾獎,並由挪威自然科學與文學院成立阿貝爾委員會負責審理。

雖然說阿貝爾獎被譽為數學界的諾貝爾獎,但表彰方向卻和諾貝爾獎不盡相同。舉例來說,諾貝爾物理學獎主要是頒發給對物理作出重要發現或發明的人,像是2020年的諾貝爾獎得主就是成功觀察到銀河系中心的超大質量緻密天體,並發現黑洞的形成是廣義相對論的確鑿預測,因而得獎。阿爾貝獎則是大多頒獎給在數學領域發展中的重要推手,也就是引領數學界的人。
今年挪威科學院將2021年的阿貝爾獎頒給匈牙利羅蘭大學(Eötvös Loránd University)的洛瓦茲·拉茲洛(László Lovász)和美國普林斯頓大學的以色列數學家阿維·威格森(Avi Wigderson),表彰他們對理論計算機科學與離散數學的貢獻,以及將兩者塑造成現代數學的重要領域。
“for their foundational contributions to theoretical computer science and discrete mathematics, and their leading role in shaping them into central fields of modern mathematics”
剪不斷理還亂的計算機科學和數學
1970年代,理論計算機科學和純數學是沒什麼關係的兩個學術領域。經過幾十年的發展,這兩個學科之間早已變得極為密切,在現代數學,我們甚至很難分清它們之間的界限。其中,洛瓦斯和威格森就是在最前線開疆闢土的人。

計算複雜性理論 (Computational complexity theory)是數學和計算機科學領域的一個重要分支。從小我們就知道算數學要快、狠、準,如何更快、更輕鬆地解決問題一直是人類追求的目標。計算複雜性理論通過引入數學計算模型計算各個演算法的資源使用情形,像是時間(透過幾個步驟產出結果)、空間(需要佔用多少記憶體),再進一步進行複雜性分類、聯絡。洛瓦茲設計的LLL演算法、威格森的去隨機化研究對拓寬和深化這個領域的貢獻無疑是最重要的領導者。
從數學到計算機科學──拉茲洛·洛瓦斯

洛瓦茲於1948年出生在布達佩斯,從小就對數學有濃厚的天份,22歲便拿到博士學位,他的早期靈感大部分來自數學家艾狄胥·帕爾(Erdős Pál)。艾狄胥的成就集中在離散關係的數學,而不是典型的連續變量上,也就是組合學、圖論等領域。
組合學(Combinatorics)、圖論(Graph theory)都是離散數學的範疇。前者主要解決組合模型中的存在、計數以及構造等方面的問題;後者作為組合學的分支,將對象之間的關係通過邊和節點組成數學結構圖。拉斯洛·洛瓦茲作為新一代數學家自然不會將離散數學侷限在純數學的理論研究中,他意識到離散數學在計算機科學中非常具有發展潛力,並著手研究離散數學可以解決計算機科學問題的方法。
最著名的研究是由洛瓦茲(Lovász)以及荷蘭數學家阿爾揚·倫斯特拉(Arjen Lenstra)和亨德里克·倫斯特拉(Hendrik Lenstra)的名字命名的LLL演算法(LLL lattice)。這種稱為LLL的算法將由整數組成的大向量分解為各種類型的最短向量的總和,也就是可以計算出空間中的點集與原點的距離。
最初的LLL演算法被應用將多項式時間(Polynomial time,P)以有理係數多項式表示,來找出他的實數近似值來解決固定維數的整數線性規劃問題。LLL演算法在數論、密碼學和通訊計算等領域也都具有顯著的應用,更是現今可以抵禦量子計算機攻擊的加密系統之一。
從計算機科學到數學──阿維·威格森

威格森於1956年出生於以色列海法。威格森最著名的成就之一就是闡明了隨機性在計算中的作用。在聊隨機性之前,我們先來聊聊什麼是P, NP:
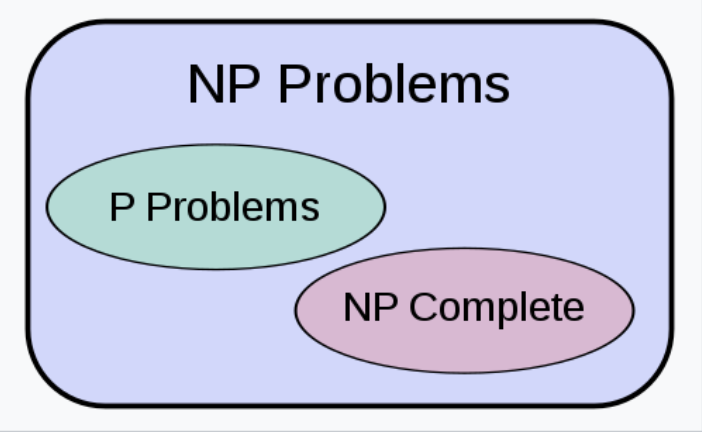
P和NP是複雜性的類別,P問題是可以快速計算出來的問題,NP問題則是可以快速驗證的問題。
當問你17乘以19是多少時,你可能沒辦法馬上心算出來,但按一按計算機就一定能得出答案,那麼這個問題就是屬於P問題,包含了所有容易解決的計算問題。現在,問你323的所有質因數有哪些呢?問題複雜了許多吧!我們必須從2、3、5……開始慢慢找,正著找質因數很困難,如果我們反著找呢?先告訴你17、19是323的質因數,是不是只要把它們乘在一起就能驗證答案對不對了?這個例子就是屬於NP問題,包含了可能是很難解決的計算問題,但只要有答案就很容易被驗證正確與否。
科學家便提出了一個看法:「會不會其實P=NP?」也就是說NP問題有可能可以被簡單解決。威格森的主要研究就是將複雜性類別一一歸位,將多項式時間演算法完全去隨機化,更快速的得到結果,並把隨機演算法和複雜性理論結合,提出P = BPP(bounded-error probabilistic polynomial time),回答了多年來對P/NP問題的疑問,大大拓寬了資訊界的未來視野。
威格森對貨幣加密的零知識證明也很有貢獻,零知識證明簡單來講就是在不透露任何資訊的情況下驗證正確性的方法。最初是在保護個資方面,像是我們想要申請某個購物網站的會員,我們就必須提供姓名、電話、出生年月日等各種資料來驗證我們的真實身份,但在零知識證明之下我們可以選擇提供「零密碼證明」、隱藏真實密碼,達到完全保護個資的目的。
有些人可能會有疑問說數學有用嗎?數學不是只能拿來算錢嗎?那你就錯了!數學一直扮演著承載科學的角色,躲在背後支持著科學發展,不難發現每一門科學都或多或少跟數學交織在一起,每一年頒發的阿貝爾獎、菲爾茲獎、諾貝爾獎都顯現出這些數學家、科學家正將科學這個巨網越織越堅固。一起為今年的得獎者送上掌聲吧!

參考資料
- The Abel Prize
- Wikipedia – László Lovász
- Wikipedia – N versus NP problem
- nature – Abel Prize celebrates union of mathematics and computer science
- 新智元導讀 – 以色列數學家威格森獲阿貝爾獎