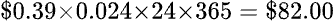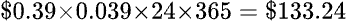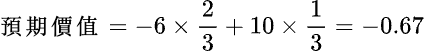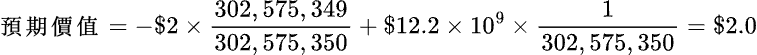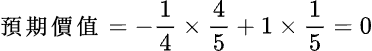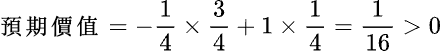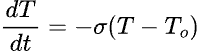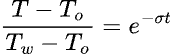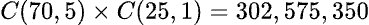樂透：一定會中獎，但機率小到不行！－《不大可能法則》

本文由 Amway 委託，泛科學企劃執行。

到底怎樣才算是「乾淨」？這不是什麼靈魂拷問，而是一個價值上億的商業命題。

在半導體產業的無塵室中，「乾淨」的定義極其殘酷：一粒肉眼看不見的灰塵，就足以讓造價數百萬美元的晶圓直接報廢。空氣品質的好壞，甚至能成為台積電（TSMC）決定是否在當地設廠的關鍵性指標。回到你的家中，雖然不需要生產精密晶片，但我們呼吸系統中的肺泡同樣精密，卻長期暴露在充滿 PM2.5、病毒以及各種揮發性氣體的環境中。為了守護健康，你可能還要付費購買「乾淨的空氣」來用。

因此，空氣議題早已超越單純的環保範疇，成為同時影響國家經濟與個人健康的重要問題。

很多人可能沒想到，無論是家用的空氣清淨機，還是造價動輒百億的頂尖晶圓廠，它們對抗污染的核心武器並非什麼複雜的雷射防護罩，而是同一件看起來平凡無奇的東西：一片外觀像紙一樣的 HEPA 濾網。但你真的相信，就憑這層厚度不到幾公分的板子，能擋住那些足以毀滅精密晶片、滲透人體細胞的「奈米級刺客」嗎？

這片大家都聽過的 HEPA 濾網，裡面到底是什麼？

首先，我們必須打破一個直覺上的誤解：HEPA 濾網（High Efficiency Particulate Air filter）在本質上其實並不是一張「網」。

細懸浮微粒 PM2.5，是指粒徑在 2.5 微米以下的污染物，它們能穿過呼吸道直達肺泡，並穿過血管引發全身性發炎。但這只是基本，在工廠與汽車尾氣中，還存在粒徑僅有 1 微米的 PM1，甚至是小於 0.1 微米的「超細懸浮微粒」（UFP，即 PM0.1）。 UFP 不僅能輕易進入血液，甚至能繞過血腦屏障（BBB），進入大腦與胎盤，其破壞力十分可怕。

如果 HEPA 濾網像水槽濾網或麵粉篩一樣，單靠孔目大小來「過濾」粒子，那麼為了攔截奈米微粒，濾網的孔目只能無限縮小到幾乎不透氣的程度。更別說在台積電或 Intel 的製程工程師眼裡，一般人認為的「乾淨」，在工程師眼裡簡直像沙塵暴一樣。對於線寬僅有 2 奈米或 3 奈米（相當於頭髮直徑萬分之一）的晶片而言，空氣中一顆微小的塵埃，就是一顆足以毀滅世界的隕石。

因此，傳統的過濾思維並非治本之道，我們需要的是原理截然不同的過濾方案。這套技術的雛形，最早可追溯至二戰時期的「曼哈頓計畫」。

HEPA 的前身，誕生於曼哈頓計畫！

1940 年代，製造濃縮鈾是發展原子彈的關鍵。然而，若將排氣直接排向大氣，會導致致命的放射性微粒擴散。負責解決這問題的是 1932 年諾貝爾化學獎得主歐文·朗繆爾（Irving Langmuir），他是薄膜和表面吸附現象的專家。他開發了「絕對過濾器」（Absolute Filter），其內部並非有孔的篩網，而是石綿纖維。

有趣的來了，如果把過濾器放到顯微鏡下，你會發現纖維之間的空隙，其實比某些被攔截的粒子還要大。那為什麼粒子穿不過去呢？這是因為在奈米尺度下，物理規則與宏觀世界完全不同。極微小的粒子在空氣中飛行時，並非走直線，而是會受到空氣分子撞擊，而產生「布朗運動」（Brownian Motion），像個醉漢一樣東倒西歪。

當粒子通過由緻密纖維構成的混亂迷宮時，布朗運動會迫使它們不斷轉彎、移動，最終撞擊到帶有靜電的纖維上。這時，靜電的吸附力會讓纖維就像蜘蛛網般死死黏住微粒。那些狂亂移動的奈米刺客，就這樣被永久禁錮迷宮中。

現在最常見的 HEPA 材料，是硼矽酸鹽玻璃纖維。

現代 HEPA 濾網最常見的核心材料為硼矽酸鹽玻璃纖維。這些玻璃纖維的直徑通常介於 0.5 至 2 微米之間，它們在濾網內隨機交織，像是一座茂密「黑森林」。微粒進入這片森林後，並非僅僅面對一層薄紙，而是得穿越一個具有厚度且排列混亂的纖維層，微粒極有可能在布朗運動的影響下撞擊並黏附在某根玻璃絲上。

除此之外，HEPA 濾網在外觀上還有一個極具辨識度的特徵，那就是像手風琴般的摺紙結構。濾材會被反覆摺疊、摺成手風琴的形狀，中間則用鋁箔或特殊的防潮紙進行結構支撐，目的是增加表面積。這不僅為了捕獲更多微粒，而是要「降低過濾風速」。這聽起來可能有點反直覺：過濾不是越快越好嗎？

其實，這與物理學中的流速控制有關。想像一條水管，如果你捏住出口，水流會變得湍急；若將出口放開並擴大，雖然總出水量不變，但出水處的流速會變得緩慢。對於 HEPA 濾網而言，當表面積越大，單位面積所需承載的空氣量就越少，空氣穿透濾網的速度也就越低。

低流速代表微粒停留在濾網內的時間也更久，增加被捕捉的機會。此外，越大的表面積也為 HEPA 濾網帶來了高「容塵量」，延長了使用壽命，這正是它能夠稱霸空氣清淨領域多年的主因。

然而，即便都叫做 HEPA 高效率空氣微粒子過濾網 (High Efficiency Particulate Air filter)，但每個 HEPA 的成分與結構還是會不一樣。例如 安麗逸新空氣清淨機 SKY ，其標榜「可過濾粒徑最小至 0.0024 微米」的污染物，去除率高達 99.99%。

0.0024 微米是什麼概念？塵蟎、花粉、皮屑或黴菌孢子，大小約在 2 至 200 微米；細懸浮微粒  PM2.5 大小約 2.5 微米，細菌也大概這麼大。最小的其實是粒徑小於 0.1 微米的「超細懸浮微粒」，大多數的病毒（如流感、新冠病毒）都落在此區間。對安麗逸新 的HEPA濾網來說，基本上通通都是可被攔截的榜上名單。

在過敏防護上，它更獲得英國過敏協會（Allergy UK）認證，能有效處理 19 大類、102 種過敏原，濾除空氣中超過 300 種氣態與固態污染物。

然而，同樣的過濾邏輯一旦進入半導體無塵室，就必須換一條更為嚴苛的技術路線。因為硼矽酸鹽玻璃纖維對晶圓來說有個致命傷，就是「硼 (Boron)」。

在半導體製程中，硼是常見的 P 型摻雜物，用來精準改變矽晶圓的電性。如果濾網有任何微小的破損、老化或化學侵蝕，進而釋放出極微量的硼離子，就可能直接污染晶圓，改變其導電特性，導致晶片報廢。

此外，無塵室要求的是比 HEPA 更極致的 ULPA（超低穿透率空氣濾網） 等級的潔淨度。ULPA 的標準通常要求對 0.12 微米 的粒子達到 99.999% 甚至 99.9999% 的超高攔截率。在奈米級的競爭中，任何多穿透的一顆微塵，都代表著一筆不小的經濟損失。

為了解決「硼」的問題並追求極限的過濾效率，材料學家搬出了塑膠界的王者，PTFE 也鐵氟龍。鐵氟龍不僅耐酸鹼、耐腐蝕，還能透過拉伸製成直徑僅 0.05 至 0.1 微米 的極細纖維，其細度遠勝玻璃纖維。雖然 PTFE 耐化學腐蝕，但它既昂貴且物理上也很脆弱，安裝時若不小心稍微觸碰，數萬元的濾網就可能報銷。因此，你只會在晶圓廠而非一般家庭環境看到它。

即便如此，在空氣濾淨系統中，還有一樣是無塵室和你家空氣清淨器上面都有的另一張濾網，就是活性碳濾網。

活性碳如何從物理攔截跨越到分子吸附？

好不容易將微塵擋在門外時，危機卻還沒有解除。因為空氣中還隱藏著另一類更難纏的大魔王：AMC（氣態分子污染物）。

HEPA 或 ULPA 這類物理濾網雖然能攔截固體微粒，但面對氣態分子時，就像是用網球拍想撈起水一樣徒勞。這些氣態分子如同「幽靈」一般，能輕易穿過物理濾網的縫隙，其中包括氮氧化物、二氧化硫，以及來自人體的氨氣與各種揮發性有機物（VOCs）。

為了對付這些幽靈，我們必須在物理防線之外，加裝一道「化學濾網」。

這道防線的核心就是我們熟知的活性碳。但這與烤肉用的木炭不同，這裡使用的是經過特殊改造的「浸漬處理（Impregnation）」活性碳。材料科學家會根據敵人的不同性質，在活性碳上添加不同的化學藥劑：

• 酸鹼中和：對付氮氧化物、二氧化硫等酸性氣體，會在活性碳上添加碳酸鉀、氫氧化鉀等鹼性藥劑，透過酸鹼中和反應將有害氣體轉化為固體鹽類。反之，如果添加了磷酸、檸檬酸等酸性藥劑，就能中和空氣中的氨氣等鹼類。
• 物理吸附與凡德瓦力：對於最麻煩的有機揮發物（VOCs，如甲醛、甲苯），因為它們不具酸鹼性，科學家會精密調控活性碳的孔徑大小，利用龐大的「比表面積」與分子間的吸引力（凡德瓦力），像海綿吸水般將特定的有機分子牢牢鎖在孔隙中。

空氣濾淨的終極邏輯：物理與化學防線的雙重合圍

在晶圓廠這種對空氣品質斤斤計較的極端環境，活性碳的運用並非「亂槍打鳥」，而是一場極其精密的對戰策略。

工程師會根據不同製程區域的空氣分析報告，像玩 RPG 遊戲時根據怪物屬性更換裝備一樣——「打火屬性怪要穿防火裝，打冰屬性則換上防寒裝」。在最關鍵的黃光微影區（Photolithography），晶圓最怕的是人體呼出的氨氣，此時便會配置經過酸性藥劑處理的活性碳進行精準中和；而在蝕刻區（Etching），若偵測到酸性廢氣，則會改用鹼性配方的濾網。這種「對症下藥」的客製化邏輯，是確保晶片良率的唯一準則。

而在你的家中，雖然我們無法像晶圓廠那樣天天進行空氣成分分析，但你的肺部同樣需要這種等級的保護。安麗逸新空氣清淨機 SKY 的設計邏輯，正是將這種工業級的精密防護帶入家庭。它不僅擁有前述的高規 HEPA 濾網，更搭載了獲得美國專利的活性碳氣味濾網。

關於活性碳，科學界有個關鍵指標：「比表面積（Specific Surface Area）」。活性碳的孔隙越多、表面積越大，其吸附能力就越強。逸新氣味濾網選用高品質椰殼製成的活性碳，並經過高溫與蒸氣的特殊活化處理，打造出多孔且極致高密度的結構。

這片濾網內的活性碳配重達 1,020 克，但其展開後的總吸附表面積竟然高達 1,260,000 平方公尺——這是一個令人難以想像的數字，相當於 10.5 個台北大巨蛋 的面積。這種超高的比表面積，是市面上常見濾網的百倍之多。更重要的是，它還添加了雙重觸媒技術，能特別針對甲醛、戴奧辛、臭氧以及各種細微的異味分子進行捕捉。這道專利塗層防線，能將你從裝潢家具散發的有機揮發氣體，或是路邊繁忙車流的廢氣中拯救出來，成為全家人的專屬空氣守護者。

總結來說，無論是造價百億的半導體無塵室，還是守護家人的空氣清淨機，其背後的科學邏輯如出一轍：「物理濾網攔截微粒，化學濾網捕捉氣體」。只有當這兩道防線同時運作，空氣才稱得上是真正的「乾淨」。

進一步了解商品：https://shop.amway.com.tw/products/2071?navigationType=brand&

隨著科技的快速進步及生活水準的不斷提高，人類在日常生活使用的工具越來越複雜。面對推陳出新，源源不絕的各種新式工具，要如何有效地使用它們呢？看到這麼多的廣告，又要如何判斷它們的真偽呢？

這些應用科學的工具固然帶來許多便利性，但是使用者在不了解背後科學原理的情況下，也可能發生誤解，造成一些錯誤觀念以訛傳訛，反而促成不必要的浪費。本文便是筆者以日常生活中的見聞，來探討生活用品背後的一些物理原理與數學，期望能釐清一些迷思，讓讀者能夠撥雲見日。

電熱水瓶

在「日常生活範式的轉變：從紙筆到 AI」一文裡，筆者提到了許多改變我們日常生活的現代科技，卻忘了非常重要的網路購物！事實上，除了菜市場外，筆者現在幾乎已不在任何商店買東西了。網路購物有一個很大的優點，那就是很容易比較不同品牌的商品。例如 2020 年筆者決定換個熱水瓶時，在美國最大的網路市場亞馬遜（Amazon）碰到一個問題：一般的熱水瓶（如松下）大約只要美金 100 左右，唯獨像印（Zojirushi）卻有高達美金 200 元以上的熱水瓶；仔細比較一下，唯一的大不同是後者有真空保溫的外層。一向節儉慣的筆者幾經思考後決定購買 4 公升裝的松下。

在透過提高裝貨運送速度、實施更嚴格的賣家驗證流程來應對假冒產品的擔憂後，中國大陸的「全球速賣通」（AliExpress） 似乎已重返美國市場，筆者最近兩、三年也開始敢在其網站購物了。數月前看到它廣告只要美金 150 元的像印真空保溫熱水瓶，一向喜歡佔小便宜的筆者就買了一隻，讓筆者有實際的數據來比較像印的高價是否值得。像印的規格資料謂保持在 90℃ 的平均功率是 24 瓦特；美國聖荷西市的電費是每一度（千瓦小時）0.39 美元，因此每年用在保溫的電費為

松下的規格資料謂保持在 88℃ 的平均功率是 39 瓦特，因此每年用在保溫的電費是

即像印熱水瓶每年可節省約 51 美元的保溫費！值不值得高價買像印熱水瓶那就看讀者準備要用多久了。筆者的松下熱水瓶用了 4 年多，因此後悔當初沒有買比較貴的像印真空保溫熱水瓶了！

一般電熱水瓶均有所謂的「節能定時器功能」：因為晚上睡覺時不用熱水，所以在睡覺前將熱水瓶關掉，可以設定幾小時後，再自動加熱，讓讀者起來時立即有熱水泡茶或沖咖啡。這看起來是很方便，但真的節能嗎？

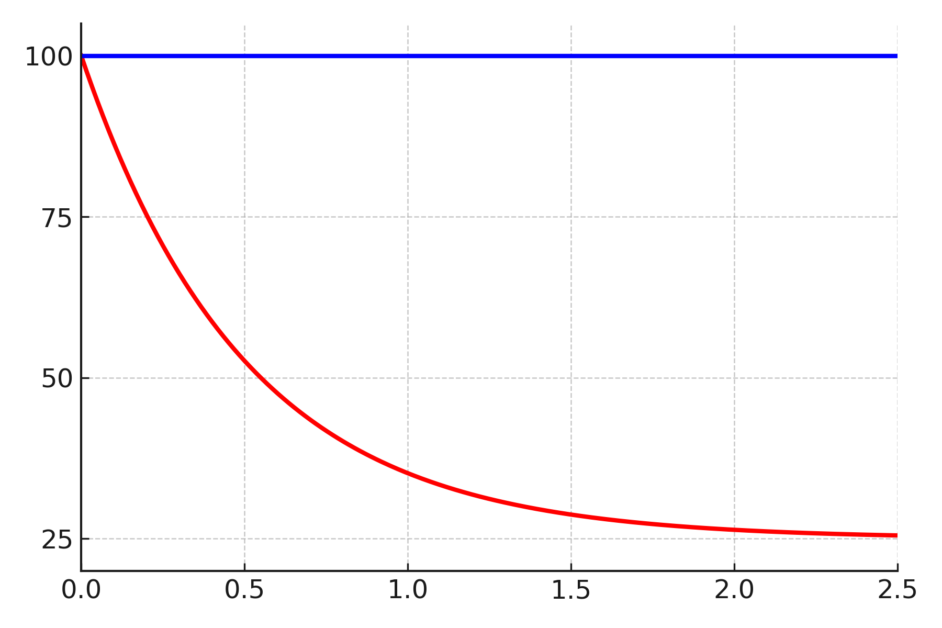
讓我們在這裡來分析一下吧。如果有科學儀器幫忙，分析將是輕而易舉；但事實上即使沒有，我們還是可以做很多有意義之分析的。我們關掉熱水瓶的電後，其溫度將類似圖一的紅線下降（註一），「最後」到達室溫。理論上「最後」應是慢慢逼近，永遠不可能達到室溫的。

但在實應上，我們可以說到達 1.5 之 x 座標時已經是室溫。而 1.5 到底是多少小時，則因電熱水瓶的設計及室溫之不同而異。如果設定的節能定時 x ≤ 1.5，那麼熱水瓶所散的熱正好由重新啟動的加熱補上，所以根本沒有節能；如果設定的 x > 1.5，則因熱水瓶在 x ≥ 1.5 後就已經不再散熱了，而沒有關掉的熱水瓶仍必須繼續保溫（圖一藍線），所以關掉熱水瓶是值得的、有節能的效果。

松下熱水瓶只有一個 6 小時的定時，筆者夏天做了一個實驗，發現 7 小時後還是室溫，所以沒用過它的「節能定時器功能」；像印松下熱水瓶在 6-12 小時間有 6 個定時。

便攜式空調

聖荷西夏天很熱的時間不長，因此筆者一直想買容易移動的「便攜式空調」（portable air conditioner），以便炎暑一過就可以收起來。以「portable air conditioner」搜尋亞馬遜網路市場，發現有價格差異很大的兩種空調：一種大約在美金 100 元以下，另一種則大約在 200 元以上。

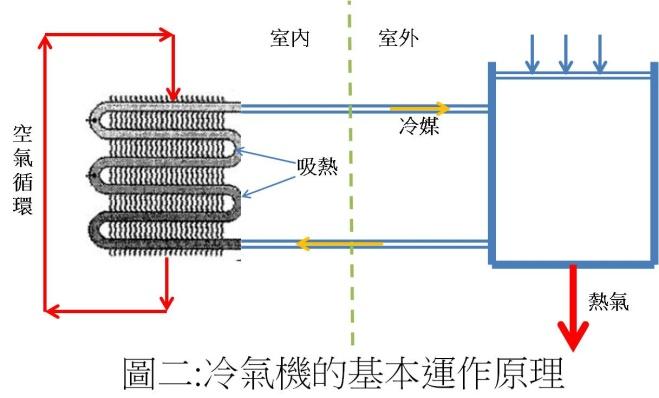
仔細「研究」發現其差異是前者不必要往外面排熱氣，後者必須有管子通到外面以便排掉熱氣。我們知道能量不滅定律，如果用電產生的熱不往外排掉，那熱只能留在房間內，房間只會越來越熱，不可能變冷的！所以這類的「冷氣機」（圖二）只能像電扇一樣，讓你在電扇前面感到涼爽而已！

事實上比電扇好一點的都加了一個水箱，利用蒸發水會吸熱，讓你感到的風比電扇更冷一點，所以價錢比普通電扇高一點。這種電扇在乾燥的地方事實上是一雙箭雕：除了吹冷風外，同時可以增加空氣的濕度；但是在濕度很高的台灣，其結果可能讓人感到更悶、更難受。

為什麼要使用水呢？除了是最常見的物質之外，水俱有許多其它物質所沒有的性質（參見「奇妙的水分子」），例如氣化熱（一克的水蒸發成一克的氣體所需的熱）、比熱（將一克的水提高溫度一度所需的熱）等等均比其它物質高出許多，所以我們馬上將看到水也常來當冷卻劑。

前面所談到之兩種空調在外表上的不同是「往外面排熱氣的管子」，在內部構造上則是「壓縮機的有無」。壓縮機將氣態冷媒擠壓成液態時會產生大量的熱，冷氣機必須透過「熱交換」將它們丟到外面去，這就是為什麼「真正的冷氣機」需要有通到外面的排氣管。被壓縮的冷媒到了壓力較低的地方會立即透過「熱交換」吸熱膨脹成氣態的冷媒。前者「熱交換」的媒體主要是室外的空氣（為了提高效力，大冷氣機會用水），後者則是室內的空氣（見圖二）。

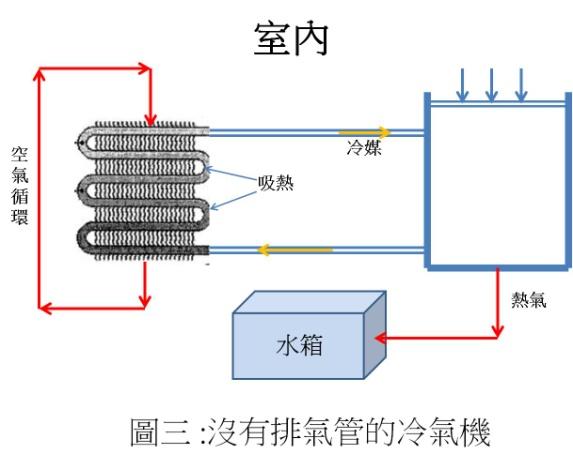
沒有排氣管的冷氣機

所以真正的冷氣機應該要有排氣管，但筆者在網路上逛店時卻發現有壓縮機、但沒有排氣管的冷氣機！例如有一款「HANLIN HS02 移動冷氣 行動空調」廣告謂：「商業級強勁壓縮機秒速制冷，快速降溫，讓酷暑瞬間消散；……。免排水高溫自蒸發系統，內建水箱設計，開機預設開啟，免排水冷凝水，高溫排風自動霧化」。從產品特色看來，壓縮機所產生的熱量應該是用來蒸發（霧化）「水箱」的水（見圖三）。讓我們在這裡利用能量不滅定律來看看是否可行。

該產品的規格謂其冷氣量為 1400 瓦特，即每秒鐘可以從室內拿掉1400焦耳的能量。前面提到水的汽化熱很高，約為每公克 2260 焦耳；因此該機器每秒鐘能蒸發掉約 0.62 公克（1400/2260）的水。也就是說為了保持室溫不變，一小時必須蒸發掉 2230 公克（2.23 公升）的水。因此除非水箱是 24 公升大，「12 小時預約定時，可設定開關機時間，方便您的生活」是絕對不可能的！還有，這些蒸發的水氣很快就會達到飽和點、結合成液態水，釋放出其剛吸收的汽化熱到室內，不可能降低室內溫度的！在廣告中他們特別介紹了「外出露營帳篷使用方法」，相信那才是該冷氣機可以真正發揮功能的地方；而商品配件中的「排水管」應該是用來「勸」我們在室內使用吧？

所以用蒸發水來冷卻壓縮機似乎是不可行的，但因為水的比熱較空氣高多了，循環「水箱」的水來冷卻壓縮機效益應該比空氣更高（見圖三），可行嗎？

DIKE 多功能移動式瞬涼水冷氣 HLE700WT就是基於這種想法的一個產品。其廣告謂：創新「無排熱管」冰風機，採用水冷循環及高效壓縮機製冷，出風降溫至 14℃，搭配獨立除溼、送風三合一功能四季都適用！前面涼快，後面涼快，無須排熱風管免窗戶施工。…製冷前需先將水箱加水，維持水循環運作，水箱裝滿 4 公升時可持續製冷 8 到 12小 時，一整天都涼爽。因為水是熱交換媒，因此廣告特別強調「大容量水箱」，讓我們在這裡也利用能量不滅定律來看看是否可行。

廣告中沒有提到冷氣量，讓我們在這裡假設與前面那款冷氣機一樣（1400瓦特）吧，即每秒鐘可以從室內拿掉1400焦耳的能量，或每小時可以拿掉5040千焦耳的能量。前面提到水的比熱很高，將1公克的水提升溫度一度需4.2焦耳；因此4公升（4000克）的水從30°C提升到100°C 水滾前可以拿掉1176千焦耳（4.2 x 4000 x 70）的熱，也就是說僅能夠拿掉冷氣機0.23小時的壓縮熱能（1176/5040）！

彩券與選擇題

美國有許多州聯合起來的「百萬大獎」（Mega Millions）：玩家可以從兩個獨立的數字池中挑選六個數字——從 1 到 70 中的五個不同數字（白球）和從 1 到 25 中的一個數字（金色百萬富翁球）。學過排列組合的讀者應該可以算出其得獎或然率是 302,575,350 之一（註二）。

美國的人口約為 335 百萬，估計絕對不會有半數以上的人買，所以其設計是每次有人中獎的機會不大，獎金下移累積，因此三不五時會出現一個大獎來製造大新聞。例如有一次大獎是 12.2 億美元，而每張「百萬大獎」券才 2 元；這麼高的「益本比」確實是相當吸引人，因此到處出現大排長龍購買，讀者會加入行列嗎？

數學及經濟學上有一稱為「預期價值」（expected value）——隨機變數可能的值，乘上其機率的總和——來幫助我們決定是否值得投資。例如假設拋硬幣正面的或然率為 2/3，反面的或然率為 1/3 ；如果擲出正面，您輸掉 $6，反面您贏得 $10；您賭嗎？這遊戲的「預期價值」為：

即平均而言，每次玩此遊戲大約會輸掉 $0.67，所以不值得玩。我們就用這個方法來看看是否值得去排長龍買「百萬大獎」吧。因為一定要買才能中獎，所以嚴格說來，在這裡不能用「預期價值」。但因為中獎幾率可以說是零，所以在這裡假設沒必要買，只是去選號碼，沒中獎時才交$2.00：

也就是說即使每次都是大獎，我們每次只要去排隊選號就可以得到$2.00。筆者雖然退休了，沒什麼大事可做，還是不會浪費時間去排隊購買的；當然，如果是因為愛國，那就另當別論了！

但是如果有 $302,575,350 將所有的組合都買下來，那不是一定可以中獎得到 $12.2 億嗎？筆者謹在此建議「泛科學」讀者成立「美國愛國獎券基金會」，募款 $302,575,350 讓我們一起發財吧（註三）！

除了投資及愛國獎券外，「預期價值」在日常生活中事實上還有一個非常有用的地方：那就是決定考試選擇題的策略。早在 1977 年當筆者還不知道什麼是投資時，就已經用常識分析了這個問題：

現行（大學入學分科測驗）倒扣的計算方法（如五選一，答對 1 分，答錯扣 0.25 分），任何只要具備簡單或然率知識的人均能算出：如果考生「完全瞎猜」，則得分數與倒扣分數剛好互相抵消。

上面這種稱為「邁可生倒扣公式」的預期價值是

在這種倒扣方法下，最佳戰略應該如何決定？顯然地，如果在五個答案中，我已經知道一個或一個以上的答案是錯的，那我應該答，因為得分的或然率已高於倒扣分的或然率：

但是如果我很不幸地「完完全全不知」呢？那因為答了也不吃虧，所以也應該答！！！總而言之，不管怎麼樣，每題都應該答！記住，每題都應該答！

「倒扣」的記分方法原有遏止考生投機的用意，可是根據上面的分析，邁可生倒扣公式不僅達不到遏止投機的目的，反而會助長之；所以，如果要避免考生猜題，倒扣比例應該提高。現在讀者應該不難算出：如果倒扣為 0.30 分，那麼邁可生倒扣公式之預期價值便變成 -0.04，就不值得瞎猜了！

結論

像印牌熱水瓶使用真空保溫，散熱率較低，也因之價格較高，但長期使用下來還是值得的。熱水瓶的「節能定時器功能」是否節能得看環境及定時長短。

「真正的冷氣機」一定要具有能「往外面排熱氣的管子」，否則因為能量不滅的關係，所有的熱只能留在室內，或許可以讓站在出風口處的人感到冷風或冷氣，但是絕對不可能使室溫下降的。事實上根本不需要分析，簡單的邏輯告訴我們：不拿熱到外面的任何機器都不可能讓室內冷下來的！筆者最後還是買了一款定價高一點、體積大很多、有管子通往外面、不怎麼方便的「便攜式空調」（註四），其冷氣量高達 4100 瓦特，為「HANLIN HS02 移動冷氣」的3倍！

美國之「百萬大獎」的「益本比」雖然可以上十億，但投資報酬率（預期價值）似乎太低，不值得浪費時間排隊去買的。如果考試選擇題採用的是「邁可生倒扣公式」，那即是完全不知道答案，也應該每題都要回答！

附註

（註一）只要透過基本微積分就可以導出來。熱水瓶的溫度（T）下降速率應該正比於散熱係數（σ）及裡外溫差（T-T_o）：

式中的 T_o 為室外溫度，解得

式中的 T_w 為熱水瓶的設定溫度（即 t=0 時的溫度）。

（註二）選一「白球」的方法有 C(70, 5) ，選五「金色百萬富翁球」的方法有 C(25, 1) ， 所以選一「白球」及五「金色球」的方法有：

（註三）筆者尚不知如何買下所有的 302,575,350 組合，請讀者提供高見。

（註四）事實上是冷暖兩用機：圖三中的室內、室外互換即成暖氣機。當暖氣機用時，因為要從室外拿熱進來，其效率比一般只在室內用電加熱的「純電熱器」高（2.7：1）。

延伸閱讀

• 「奇妙的水分子」，科學月刊，1979年1月。
• 「聯考與選擇題」，科學月刊，1977年8月。
• 「日常生活中的物理與化學」，科學月刊，2010年12月。
• 「日常生活範式的轉變：從紙筆到 AI」，泛科學，2023/03/08。
• 《我愛科學》，華騰文化有限公司，2017年12月出版；內含「奇妙的水分子」、「聯考與選擇題」、「日常生活中的物理與化學」。

理解期望值，有助於分析賭場裡的大部分賭局，以及美國中西部和英國的嘉年華會中，常有人玩、但一般人比較不熟悉的賭法：骰子擲好運（chuck-a-luck）。

招攬人來玩「骰子擲好運」的說詞極具說服力：你從 1 到 6 挑一個號碼，莊家一次擲三顆骰子，如果三個骰子都擲出你挑的號碼，莊家付你 3 美元。要是三個骰子裡出現兩個你挑的號碼，莊家付你 2 美元。

假如三個骰子裡只出現一個你挑的號碼，莊家付你 1 美元。如果你挑的號碼一個也沒有出現，那你要付莊家 1 美元。賽局用三個不同的骰子，你有三次機會贏，而且，有時候你還不只贏 1 美元，最多也不過輸 1 美元。

我們可以套用名主持人瓊安．李維絲（Joan Rivers）的名言（按：她的名言是：「我們能聊一聊嗎？」），問一句：「我們能算一算嗎？」（如果你寧願不算，可以跳過這一節。）不管你選哪個號碼，贏的機率顯然都一樣。不過，為了讓計算更明確易懂，假設你永遠都選 4。骰子是獨立的，三個骰子都出現 4 點的機率是 1/6×1/6×1/6＝1/216，你約有 1/216 的機率會贏得 3 美元。

僅有兩個骰子出現 4 點的機率，會難算一點。但你可以使用第 1 章提到的二項機率分布，我會在這裡再導一遍。三個骰子中出現兩個 4，有三種彼此互斥的情況：X44、4X4 或 44X，其中 X 代表任何非 4 的點數。而第一種的機率是 5/6×1/6×1/6＝5/216，第二種和第三種的結果也是這樣。三者相加，可得出三個骰子裡出現兩個 4 點的機率為 15/216，你有這樣的機率會贏得 2 美元。

同樣的，要算出三個骰子裡只出現一個 4 點的機率，也是要將事件分解成三種互斥的情況。得出 4XX 的機率為 1/6×5/6×5/6＝25/216，得到 X4X 和 XX4 的機率亦同，三者相加，得出 75/216。這是三個骰子裡僅出現一個 4 點的機率，因此也是你贏得 1 美元的機率。

要計算擲三個骰子都沒有出現 4 點的機率，我們只要算出剩下的機率是多少即可。算法是用 1（或是100％）減去（1/216 +15/216 + 75/216），得出的答案是 125/216。所以，平均而言，你每玩 216 次骰子擲好運，就有 125 次要輸 1 美元。

這樣一來，就可以算出你贏的期望值（$3×1/216）+（$2×15/216）+（$1×75/216）+（–$1×125/216）＝$（–17/216）＝–$0.08。平均來說，你每玩一次這個看起來很有吸引力的賭局，大概就要輸掉 8 美分。

尋找愛情，有公式？

面對愛情，有人從感性出發，有人以理性去愛。兩種單獨運作時顯然效果都不太好，但加起來⋯⋯也不是很妙。不過，如果善用兩者，成功的機率可能還是大一些。回想舊愛，憑感性去愛的人很可能悲嘆錯失的良緣，並認為自己以後再也不會這麼愛一個人了。而用比較冷靜的態度去愛的人，很可能會對以下的機率結果感興趣。

在我們的模型中，假設女主角——就叫她香桃吧（按：在希臘神話中，香桃木﹝Myrtle﹞是愛神阿芙蘿黛蒂﹝Aphrodite﹞的代表植物，象徵愛與美）有理由相信，在她的「約會生涯」中，會遇到 N 個可能成為配偶的人。對某些女性來說，N 可能等於 2；對另一些人來說，N 也許是 200。香桃思考的問題是：到了什麼時候我就應該接受X先生，不管在他之後可能有某些追求者比他「更好」？我們也假設她是一次遇見一個人，有能力判斷她遇到的人是否適合她，以及，一旦她拒絕了某個人之後，此人就永遠出局。

為了便於說明，假設香桃到目前為止已經見過 6 位男士，她對這些人的排序如下：3—5—1—6—2—4。這是指，在她約過會的這 6 人中，她對見到的第一人的喜歡程度排第 3 名，對第二人的喜歡程度排第 5 名，最喜歡第三個人，以此類推。如果她見了第七個人，她對此人的喜歡程度超過其他人，但第三人仍穩居寶座，那她的更新排序就會變成 4—6—1—7—3—5—2。每見過一個人，她就更新追求者的相對排序。她在想，到底要用什麼樣的規則擇偶，才能讓她最有機會從預估的 N 位追求者中，選出最好的。

要得出最好的策略，要善用條件機率（我們會在下一章介紹條件機率）和一點微積分，但策略本身講起來很簡單。如果有某個人比過去的對象都好，且讓我們把此人稱為真命天子。如果香桃打算和 N 個人碰面，她大概需要拒絕前面的 37％，之後真命天子出現時（如果有的話），就接受。

舉例來說，假設香桃不是太有魅力，她很可能只會遇見 4 個合格的追求者。我們進一步假設，這 4 個人與她相見的順序，是 24 種可能性中的任何一種（24＝4×3×2×1）。

由於 N＝4，37％ 策略在這個例子中不夠清楚（無法對應到整數），而 37％ 介於 25％ 與 50％ 之間，因此有兩套對應的最佳策略如下：

（A）拒絕第一個對象（4×25％＝1），接受後來最佳的對象。

（B）拒絕前兩名追求者（4×50％＝2），接受後來最好的求愛者。

如果採取A策略，香桃會在 24 種可能性中的 11 種，選到最好的追求者。採取 B 策略的話，會在 24 種可能性中的 10 種裡擇偶成功。

以下列出所有序列，如同前述，1 代表香桃最偏好的追求者，2 代表她的次佳選擇，以此類推。因此，3—2—1—4 代表她先遇見第三選擇，再來遇見第二選擇，第三次遇到最佳選擇，最後則遇到下下之選。序列後面標示的 A 或 B，代表在這些情況下，採取 A 策略或 B 策略能讓她選到真命天子。

1234；1243；1324；1342；1423；1432；2134（A）；2143（A）；2314（A, B）；2341（A, B）；2413（A, B）；2431（A, B）；3124（A）；3142（A）；3214（B）；3241（B）；3412（A, B）；3421；4123（A）；4132（A）；4213（B）；4231（B）；4312（B）；4321

如果香桃很有魅力，預期可以遇見 25 位追求者，那她的策略是要拒絕前 9 位追求者（25 的 37％ 約為 9），接受之後出現的最好對象。我們也可以用類似的表來驗證，但是這個表會變得很龐雜，因此，最好的策略就是接受通用證明。（不用多說，如果要找伴的人是男士而非女士，同樣的分析也成立。）如果 N 的數值很大，那麼，香桃遵循這套 37％ 法則擇偶的成功率也約略是 37％。接下來的部分就比較難了：要如何和真命天子相伴相守。話說回來，這個 37% 法則數學模型也衍生出許多版本，其中加上了更合理的戀愛限制條件。

——本書摘自《數盲、詐騙與偽科學》，2023 年 11 月，大牌出版，未經同意請勿轉載。