本文原文刊登時間為2020年11月6日,原文標題為《什麼是抽樣誤差?為何外國媒體報導的與老師教的不一樣?》
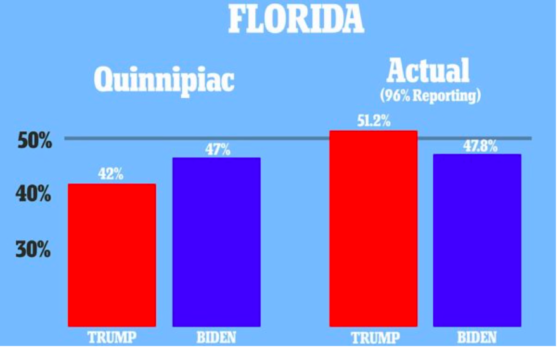
美國總統大選進入最後一周時,許多媒體紛紛在搖擺州進行民調,其中佛羅里達是選情極其緊繃的大州。

華盛頓郵報-ABC於10/24-10/29在該州民調的結果顯示:在 824 位可能投票的選民中,川普領先拜登 50−48個百分點,因為抽樣誤差為 ± 4.0 %,報導結論佛州選情難分難解。紐約時報於10/27-10/31在該州民調的結果則顯示:在1,451位可能投票的選民中,拜登領先川普47−44個百分點,其抽樣誤差為 ± 3.2%。
兩個民調相隔只 2−3 天,拜登從落後 2 個百分點轉為領先 3 個百分點,這領先程度有統計顯著性嗎?(佛州開票 96% 的結果是川普 51.2% 拜登 47.8%)
這裡有兩個相關問題要先解決:
- 第一、樣本數 N=1,451 為何抽樣誤差是 ±3.2%?這個數字對嗎?一般民調若樣本數在N=1,000左右,抽樣誤差不是大約 ±3% 嗎?為何紐時的樣本數高達 N=1,451,抽樣誤差不是更低?反而更高?
- 第二、如果抽樣誤差低於±3%,那拜登在佛州領先川普超過抽樣誤差,便可以說這差距有統計顯著性嗎?
什麼是「抽樣誤差」?
首先解釋第一個問題:所謂「抽樣誤差」(margin of error)的是當母體比例為π時,重複抽取許多樣本所得樣本比例 P 的標準差乘以 1.96。更詳細地說:當母體比例為π時,重複抽取許多樣本數為 N 的樣本會得到許多不同的P值,這些 P 值的分佈稱作 P 的「抽樣分佈」(sampling distribution)。
根據中央極限定裡,P 的抽樣分佈是以π為中心的常態分佈,其變異量是 π(1-π)/N。我們若以π為中心取一個區間(π-m, π+m)讓 P 落在區間內的機率為 95%,則代表此區間寬度的 m 即為 95% 信心水平之下的抽樣誤差,其公式為:
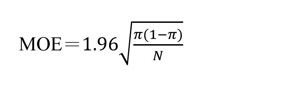
雖然這個公式可以適用於任何的π值,在沒有特別資訊的情況下,一般以 π=0.5 來計算 MOE。
舉例來說,聯合報在 2019 年 12 月 12-14 日實施了一個民調,它在報導中特別就調查方法報告如下:
「調查於十二月十二日至十四日晚間進行,成功訪問一千一百一十位合格選民,另二百九十一人拒訪;在百分之九十五信心水準下,抽樣誤差正負三點零個百分點以內。採全國住宅及手機雙電話底冊為母體作尾數隨機抽樣,藉由增補市話無法接觸的唯手機族樣本改善傳統市話抽樣缺點,調查結果依廿歲以上性別、年齡及縣市人口結構加權,調查經費來自聯合報社。」
同樣的,蘋果日報在報導其於 2019 年12月27-29 實施的民調時也提到:
「本次民調由《蘋果新聞網》委託台灣指標公司執行,經費來源是《蘋果新聞網》,調查對象為設籍在全國22縣市且年滿20歲民眾,調查期間為12月27日至29日,採用市內電話抽樣調查,並使用CATI系統進行訪問。市內電話抽樣依縣市採分層比例隨機抽樣法,再以電話號碼後2碼隨機抽出,成功訪問1,069位受訪者,在95%信心水準下,抽樣誤差為±3.0%。」
依上述公式分別代入 N=1,110 及 N=1069 可得 MOE=2.94%、3.00%,正是報導所說的「抽樣誤差正負三點零個百分點以內」、「抽樣誤差為 ±3.0%」。
紐時在佛州的選前最後民調的樣本數 N=1,451 要高出 1,110 甚多,為何它所報告的抽樣誤差反而較大?我們若把 N=1,451 套入上式,不是應該得到 MOE=2.57%嗎?為何紐時說是 3.2%?
其實不只紐時,華郵/ABC 民調的抽樣誤差 4.0% 也超過了以 N=824套入上式所算得的 3.41%。為何美國媒體計算民調抽樣誤差與基本統計學教科書所教的算法不一樣?華郵/ABC在描述其民調方法時特別強調其抽樣誤差是在「納入設計效應」(including design effects)之後計算所得;什麼是「設計效應」?
什麼是「設計效應」?
這個問題牽涉到「有效樣本數」(effective sample size)的概念。所謂「有效樣本數」並不是統計分析中除去遺漏值之後的「有效N」(valid N),而是在調整受訪者代表性之後的「加權樣本數」(weighted sample size)。
下面我會說明:紐時所報告的抽樣誤差其實是根據「有效樣本數」調整過的抽樣誤差,也就是納入設計效應之後算得的抽樣誤差。
一般民調樣本因為不是使用「簡單隨機抽樣」(simple random sampling)得到的結果,母體中每人被抽到的機率並不一致。因此,樣本中某些族群的代表性並不能反映它們在母體中的代表性。為了讓各族群在樣本中的代表性和母體一致,樣本必須經過加權處理。上述聯合報和蘋果日報的報導便報告了它們民調的抽樣設計和加權的概略步驟。一般民調機構會把加權所使用的權重存為資料中的一個變數,其數值代表樣本中每個受訪者所代表族群的權重。
例如「台灣選舉與民主化研究」2020年民調資料合併檔(TEDS2020)中便有這樣的一個權值變數w,它的值介於0.295至3.474之間,其變異範圍反映了各族群在原樣本中的代表性與它們在母體中的代表性差異的程度。
由於加權的關係,原來的樣本數已不能有效反映加權後的樣本數,因此有所謂「有效樣本數」(effective sample size)的概念,有效樣本數的計算方式因加權方式而異,抽樣理論大師 Leslie Kish 建議了一個粗略的算法:
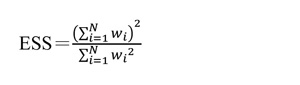
除非根本沒有加權,否則這個公式一定小於N,也就是加權後的有效樣本數會比原樣本數小。以TEDS2020原樣本數N=2,847為例,ESS=2,359,也就是加權後的有效樣本數只有原樣本數的83%。
我們如果以加權後的有效樣本數來計算抽樣誤差,則調整後的抽樣誤差會比根據原樣本數算出的抽樣誤差還大。這個差異,可以說是因為實際樣本之抽樣設計背離簡單隨機抽樣而造成的結果,我們定義「設計效應」(design effect)為:

由於抽樣誤差之平方與樣本數成反比,上式也可導出:

再以TEDS2020為例,DE=1/0.83=1.21。換算可以得到加權後的抽樣誤差是原抽樣誤差的 1.1 倍。
跟據紐時所報告的加權後的抽樣誤差以及由原樣本數所算出的簡單隨機抽樣之抽樣誤差,我們可以算出佛州民調的設計效應:
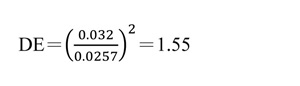
這設計效應比TEDS2020要高出很多!這可能是因為TEDS採用分層隨機抽樣面訪,其設計比起新聞媒體採用電話+手機有所不同。有了設計效應的估計值,我們就可以算紐時佛州民調的有效樣本數了:它的 ESS=936,只有原樣本數的三分之二。相對而言,華郵/ABC的佛州民調的設計效應是 DE=1.37,其有效樣本數是ESS=600.
如果我們以 N=936 算基於簡單隨機抽樣設計的抽樣誤差,它會恰恰是紐時所報告的 3.2%。以 N=600 來算的話,抽樣誤差就剛好是ABC/華郵所報告的 4.0%。
值得注意的是: 如果紐時效仿聯合報用原樣本數 N=1,451 計算抽樣誤差,這2.57% 的誤差值可能會讓很多讀者誤以為拜登領先川普的三個百分點已經超過超過抽樣誤差,因而具有統計上的顯著性。紐約時報的分析家沒有這樣做,這是他們的嚴謹之處。
以有效樣本數算候選人支持度差距的顯著性
然而選舉用的對比式民調還有第二個問題:一般媒體通常只報告單一比例的抽樣誤差,而對比式民調著重的不是單一比例,而是兩位候選人所獲支持度比例的差距。此差距的抽樣誤差與單一比例的抽樣誤差完全不一樣,它可以達到單一比例抽樣誤差的兩倍或更多。
關於對比式選舉民調的抽樣誤差,我曾寫過一篇文章指出一般媒體在報導時的錯誤解讀,並提出一個計算正確抽樣誤差的公式。
這篇文章請見:對比式選舉民調的錯誤解讀
佛州民調結果拜登領先川普47−44。我們現在可以用有效樣本數來算拜登領先差距的抽樣誤差了。我在網上提供了一個速算表歡迎讀者下載使用。
計算的結果是抽樣誤差高達 6.03 %:拜登領先的差距其實還在誤差範圍之內。
注意:如果以原樣本數 N=1,451 代入速算表,則抽樣誤差為 4.91%,比 6.03% 要小得多。
關於民調報導,還有很多進步空間
台灣的媒體在報導對比式民調的結果時,似乎都像聯合報、蘋果日報一樣報告以「簡單隨機抽樣」為假設的單一比例抽樣誤差,而未考慮設計效應。這個抽樣誤差本來就太小,再加上對比所產生的問題,可以說是雙重的誤導!
外國媒體的民調報導近年來有進步。除了一般會報告根據設計效應調整過的抽樣誤差以外,有些民調機構也報告了對比式民調抽樣誤差的正確解讀方式。有興趣的讀者可以參考 Pew Research Center 這篇解釋抽樣誤差的文章:5 Key Things to Know about the Margin of Error in Election Polls