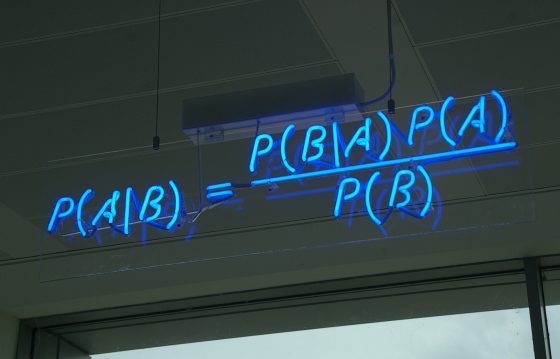先前介紹完貝氏定理後,有讀者反應講太快,應該先解釋貝氏定律裡最重要的觀念——條件機率。機率量化了一件事情發生的可能性。而條件機率嘛,比如說,你家樓下住了一位每天慢跑10公里的爺爺,傍晚你們在樓梯間遇到
「爺爺明天70歲生日嗎,都看不出來哎~」
爺爺能順利切到70歲蛋糕的機率,鐵定比台灣人平均能活到70歲的機率大上許多,因為健康的他只要再活一天就可以了。
給定某個條件下某個事件發生的可能性,即稱為條件機率。如果還不清楚,請想像這樣的場景:
※

星期五傍晚,珮穎獨自走在夕陽下。她晚上沒行程,只是單純不想加班。她討厭現在的公司文化,老闆總喜歡把員工綁在公司,綁越久越好。
又不是定存,放著也不會生利息。
她想起離開時,主管的視線越過隔板上方盯著她,心裡忍不住埋怨。
從馬路轉入小巷子,單行道兩側停滿車子,前方路口有個攤販在準備營業。一位穿西裝的上班族經過攤販,彎進巷子裡。逆光的夕陽將男子剪成一片瘦高的黑影,走近點,他的臉孔從黑影中浮現,一對修長秀氣的眼睛,以男生來說算白的膚色,給人秀氣的感覺,但不是柔弱,是無論面對甚麼事情,彷彿都能從容不迫處理的氣質。
珮穎注意到他的識別證還掛在身上,正想偷瞥一眼,男子突然加快腳步閃進路旁兩台車的縫隙間,對珮穎招手。
嗯?
還沒反應過來,珮穎聽見身後引擎聲響。回頭一看,一台老舊發財車要通過。男子還在對自己招手,遲疑一會兒,珮穎也縮進兩台車的縫隙間。
「我跟妳換位子吧。」
他高舉包包,與珮穎擦身而過,一陣清新的木香調香水氣味傳來。發財車捲起灰塵離去,男子揮揮手咳了幾聲。珮穎這下看清楚他的識別證了。
那年珮穎25歲,子威29歲。距離台灣男女平均壽命,各自還有57年與47年。
※
星期五傍晚,珮穎在夕陽下踱步,落日的餘溫被玻璃隔絕在外,窗戶這側只剩冰冷的空調,醫療儀器的聲響替時間畫下一道道刻度。珮穎坐回病床旁,病房裡總是充滿消毒水的氣味,但一靠近子威,還是可以聞到那股木香調的香水氣味。
子威伸過手來握住珮穎,兩人相視微笑。只要看見夕陽,珮穎就會想起他們第一次見面的畫面,這點子威比誰都清楚。
「50年了,這一切過得真快。」
這一年,珮穎75歲,距離台灣女性平均壽命還有7年;子威79歲,超過男性平均壽命3年。
※
巷子裡邂逅後,他們陷入熱戀。2年後的婚禮上,子威開頭第一句話是
「我要謝謝一位發財車司機——」
他們擁有標準的平凡的幸福的生活。生兒育女,儘管偶爾免不了吵架,但只要一到傍晚,總有一方會提議去散步,然後在夕陽下言歸於好。幾十年過去,小孩成家。雖然退休了,他們還得幫忙帶孫子。又過了幾年,孩子總算將孫子接回去自己帶。
那年子威72歲,珮穎68歲。
正準備好好享受生活,子威卻突然診斷出罹患癌症。美好的生活像紙糊似的,輕易地被命運撞出一個大洞。

剛知道病情時,子威很消沉,一度想放棄治療。
「李子威,你滿腦子想死就去死好了!我告訴你,台灣男人平均壽命是76歲,你才72歲,最好你打算這麼丟臉,讓你老婆比別人多守4年寡!」
說到最後,珮穎分不清自己是在罵人還是在哭泣。子威坐在客廳沙發,一整晚沒回話。隔天傍晚他們去散步,子威給珮穎看了他今天去醫院的診斷報告。一小時後,他住院接受癌症療程。
當晚,珮穎靠在病床上的子威替他削水果。
「第一次見面時,我不是走到前面幫妳擋灰塵嗎?」
珮穎點點頭。子威繼續說
「其實啊,我一直都沒講,當時我有刻意從妳的左側走過去噢。」
「啊?」
「因為心臟在左側,人通常是右撇子,身子會無意識往左傾斜。走在妳左側,妳會錯以為,怎麼自己一直往我身上靠,是不是喜歡我。」
「聽你亂說。」
珮穎嗤嗤地笑著,子威露出認真的表情
「真的,不然為什麼我們跑步都逆時針呢?就是逆時針跑時,靠左傾斜會自動產生向心力,跑起來比較順。」
珮穎半信半疑,卻看到子威似笑非笑地盯著自己,珮穎這才發現自己左半邊靠在子威身上。
「那麼老了還開這種玩笑。」
珮穎作勢打他,但她心底明白,子威是故作若無其事,想讓她安心。儘管受到影響,但他已經恢復成原本那位替她著想,總是把她擺在比自己更重要地位的男人。
※

「這幾年辛苦妳了。」
子威拿下氧氣罩,氣若游絲,距離診斷出癌症的那天到現在過了7年,前天他才剛從加護病房出來。醫生覺得子威能活到現在已經是奇蹟了。
珮穎知道這才不是奇蹟,是子威堅強意志力的展現。
「你才辛苦,已經超過平均壽命3年了,你做的很棒。」
珮穎開玩笑地說。子威搖搖頭,眼神望向床頭櫃上的筆記本,珮穎替他拿過來,裡面滿滿的數學式子
「還沒,我還沒贏過我這年紀的預期平均壽命。」
「你這年紀的平均壽命?」
子威休息了一下,一個字一個字慢慢說
「我後來才知道,平常說的是平均壽命是指『剛出生時所預期的平均壽命』,是最短的預期平均壽命。隨著年紀,我們預期能夠活的平均壽命就會慢慢變長。」
「為什麼?」
珮穎不懂,平均壽命就是平均壽命,怎麼會隨著年齡改變呢?
「舉個例子來說,4個同時出生的人,各自活到4歲、10歲、60歲、70歲。這樣平均壽命是幾歲?」
「36歲。」
「5歲時,剩下3個人,這3人的平均壽命是46.7歲。」
子威停下來喘口氣,現在他的光說話就得費上很大的力氣。
「換句話說,給定活到5歲時,平均壽命從剛出生的36歲,提升到46.7歲。增加了10.7年。」
「聽起來有點像條件機率?」
珮穎回答,他們夫妻的數學都不錯。
「年紀越大,樣本空間裡年輕早逝的人被排除在外,我們預期他們能夠活的平均壽命就會越來越長。假設y是表示壽命的隨機變數,則x歲時的壽命期望值為,」
筆記本上寫著
「其中,P(y|x)是指給定x歲的人,壽命為y歲的條件機率。只要活到40歲,能活到70歲的機率就會比20歲時能活到70歲的機率更大。用數學式子表示是P(y=70|x=40) > P(y=70|x=20)。」
子威接過筆記本,翻頁又是一大堆算式。
「我們再來定義一個『x歲的平均餘命』,意思是x歲的人平均還能再活幾年。它的數學式子是,」
他指著第二個加總符號說
「取k’=k+1,可以得到結果為,」
「換句話說,x歲的平均餘命,就是把『給定x歲後,還會活k年的機率』,從k=1到k=∞累加起來。」
子威笑了,那笑容像在草地裏撿到彈珠的小男孩,跑回來跟朋友炫耀的表情。
「我查過了台灣官方的國民生命表。在我這年紀的男性……竟然平均餘命還有8.3年。照你的標準來要求…我還有8年要努力呢……做你的老公……真辛苦。」
子威突然一陣咳嗽,笑容還沒褪去,痛苦的表情湧上混雜在一起。珮穎眼前一陣模糊,她知道子威又在安慰她了。她吸了吸鼻子,試圖讓聲音平穩
「那就辛苦你了,請再為了我多活幾年。」
當晚半夜,子威緊急被送回加護病房。凌晨,珮穎簽下放棄急救同意書。
※

星期五傍晚,珮穎站在夕陽下。紙蓮花被包覆在更大的、火焰形成的蓮花中。已經過了好幾次夕陽,她卻還沒跟子威說到話。這次的冷戰好久。
應該不可能習慣身邊沒有子威吧。不,不是不可能習慣,是我不希望習慣。
「奶奶妳還好嗎?」
孫女打斷了珮穎的思緒。
「爺爺還在的。只是我們看不到而已。」
孫女安慰她。珮穎想起她們相遇時,她正是孫女這個年紀吧。
「奶奶妳搬過來跟我們住好了,這樣爺爺也不用跑太多地方,可以更常回來。」
孫女試探性地問。珮穎知道孫女擔心獨居的自己觸景生情。有很多案例,感情深厚的夫妻一個先離開,另一個走不出來,也很快離開了。
「妳放心,奶奶很堅強,可以照顧好自己,還能活很多年的。妳爺爺教過我一套觀念……」
珮穎向孫女解釋起應用到條件機率的平均餘命。
「照你爺爺的說法,我還有11年好活。太早去鐵定會挨妳爺爺罵的。」
一旁還在念高中的小孫子插嘴說道
「可是奶奶,這觀念有點奇怪,因為機率恆正,不管到幾歲,平均餘命永遠是正的,表示當下的預期平均壽命永遠會大於當下的年紀,那不就是說,人類可以永遠活下去——」
「你閉嘴啦!」
孫女出言制止她那搞不清楚狀況的弟弟。
的確,這聽起來有點像芝諾悖論:烏龜跟阿基里斯賽跑,每當阿基里斯快要追上烏龜,烏龜都會趁著阿基里斯追趕所花的時間,再往前移動一點,阿基里斯又得再追趕。不論靠多近,烏龜永遠有一小段時間可以再前進,阿基里斯永遠追不上烏龜。
小孫子沒說錯,給定現在的年齡,只要沒破人瑞紀錄,永遠有人活得更久。平均餘命永遠大於零,永遠可以活下去。
但跟芝諾悖論不一樣,芝諾悖論有數學上的問題;餘命的觀念儘管看起來不合理,但在數學上完全正確,沒有漏洞。餘命永遠恆正,但那終究只是期望值,還是會有很多人在沒活到那年紀之前就先離開。
這是體貼的子威留給她最後的禮物,一道用完美數學構成的甜言蜜語。
他的意思是,他將永遠陪在她身邊。就像第一次見面一樣,他告訴她車來了,體貼地閃到前方幫她擋灰塵。
「奶奶自己住沒關係,」
珮穎打斷了孫女與孫子的爭執
「這樣爺爺如果回家了,才有人幫他開門啊。」
她朝左望去,夕陽在腳下拉出一道長長的影子,她閉上眼睛,彷彿聞到了子威身上那股淡淡的木香調香水氣味。
註: 更多賴以威的數學故事,請參考《超展開數學教室》

註:更多賴以威的數學故事,請參考《超展開數學教室》。

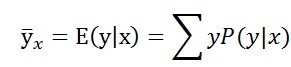
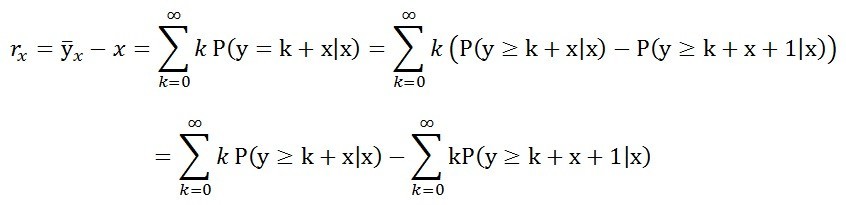
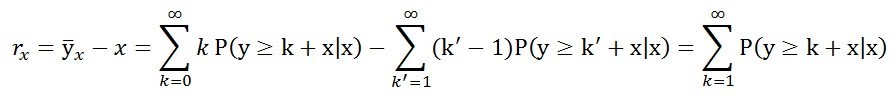





























 ——本文摘自《
——本文摘自《