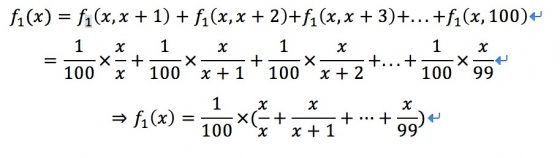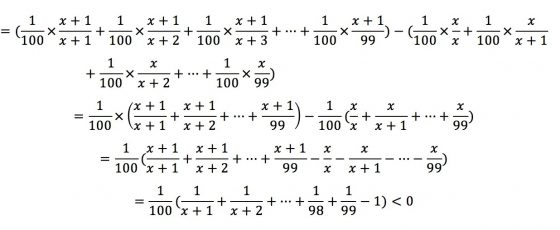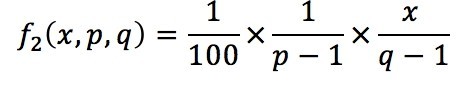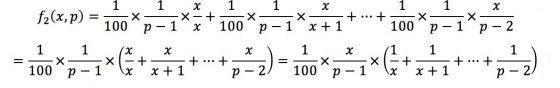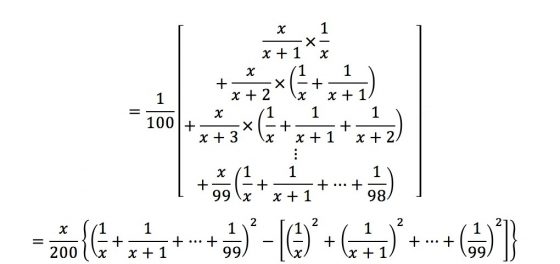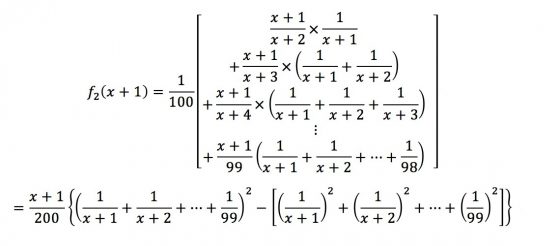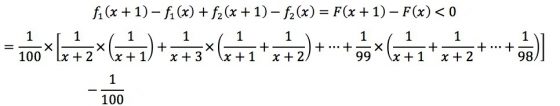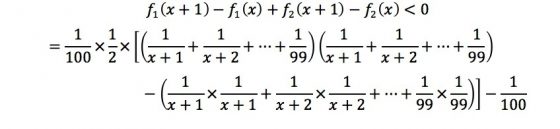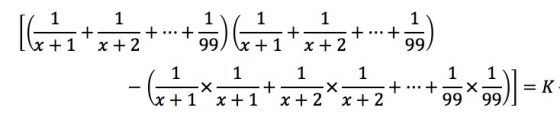「數感盃青少年寫作競賽」提供國中、高中職學生在培養數學素養後,一個絕佳的發揮舞台。本競賽鼓勵學生跨領域學習,運用數學知識,培養及展現邏輯思考與文字撰寫的能力,盼提升臺灣青少年科普寫作的風氣以及對數學的興趣。
本文為 2019數感盃青少年寫作競賽 / 高中組專題報導類銅獎之作品,為盡量完整呈現學生之作品樣貌,本文除首圖及標點符號、錯字之外並未進行其他大幅度編修。
- 作者:蕭宇岑、林子揚/中正高中。

愛情或婚姻,到底有沒有所謂的真命天子?大部分的人應該都希望自己能夠遇到一個完美情人,並和他長相廝守。有些人會特別去算命,算算自己會在什麼時候會遇到自己的真命天子;有些人會因為時間壓力而訂一個期限,要在這期限內找到對象,不然就不結婚;而現代社會,更有些人會為了盡快找到結婚對象,而去相親,不論是自己願意,還是被父母逼的。
愛情這種東西,很多人都會說要「看緣分」,也就是說,大部分的人相信,找到另一半是很難掌握的。為了更容易掌握住自己的愛情,人們就會出現去算命、聯誼,乃至於相親的行為了。但是,在這些方式之中,我們是否能透過數學的觀點,得到一個合理的策略,例如當我們在進行相親時,是否能夠透過機率的方式去計算,產生一個最好的策略去選中最好的那位完美情人呢?
我們假設要和100個對象相親(約會),而且每次約會後都必須做決定,就是選擇和他繼續交往或者不繼續,若選擇不繼續發展,也就表示放棄了這個對象,則可以繼續和下一個人相親(約會);若選擇了交往,就不能反悔、不可重新選擇和繼續約會。
若這一百個人我們可以排出名次,也就是說他們有大小關係,而且任兩人不並列,那麼如何才能夠使你有最大的可能選中這100個對象中最好的那一位呢?(先決條件為:只有一個最好的,且只要選最好的。)
在這裡我們運用數學的「最佳停止理論」:先在前期設定一個期間(淘汰期),這個期間我們將他設為評判標準,也就是說在這期間之內,不論遇到多好的對象都必須放棄,可是過了這個期間之後你擁有了足夠評判標準,因此只要在此後有遇上比這淘汰期任何人還好的對象,也就是目前為止遇到最好的人,則可以直接選擇他。所以這個期間的長短的取捨,其實就是我們選取的策略。
首先假設最好的對象是在第 p 個的位置,在 100 人中他恰好為最好的對象的機率為 1/100 (只有一個最好的對象)。再來假設淘汰期為 x 個人,也就是淘汰掉 x 個人。而為了達成我們的最終目的:選中最好的。在遇到 P 之前,從第1位到第 P−1 位內最好的人,就必須介在第1到第x間(淘汰期內),被當成選出 p。的標準,也就是說他被淘汰掉。如此一來,就能在x後,準確地選中最好的對象( p。)。
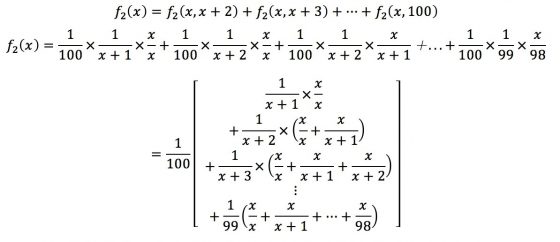
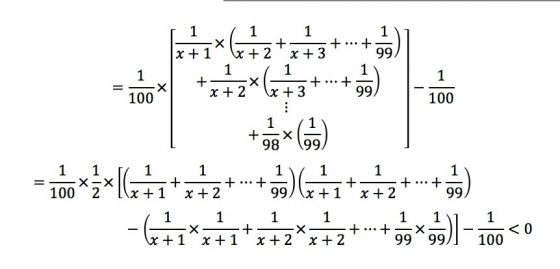
故以為x, p 為變數, p為最好且選中p之機率函數為:
當固定淘汰 x 人後,考慮p的位置。當 p。在淘汰期(x)內時,我們選中他的機率便為0,故只需要考慮p=x+1一直到p=100的時候。選中最好的對象的機率為f1(X)為:
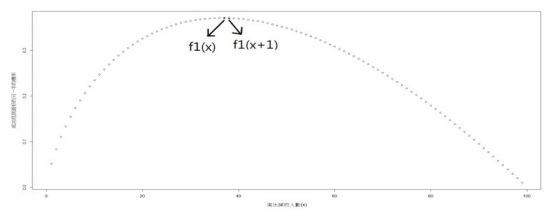
讓我們思考一下,剛開始隨著x(淘汰期)的增加,我們有更好的標準,故選中最好的機率f1(X)的函數圖形是遞增的,但是當x超過某數時,不但會造成標準過高,還會造成選擇變少,故此時選中最好的機率f1(X)會變成遞減。故可推估隨著x值的變大,機率會先增加後減少,而我們需要最大的機率(f1(X)成最大值),所以考慮x的後項(x+1)會恰好剛比前項(x)還差的情況(代入函數後相減為負),且為最小值以數學式表示:
f1(x+1)−f1(X)且 x 為最小值
經過我們帶入數字計算,發現 x為 37 有最大的機率 37.1042 %,也就是說我們將前 37 個淘汰做為標準,則我們就會有約 37 %的機會選到最好的對象。
但是!37 %⋯⋯顯示出有將近六成的機率會失敗,並且若最好的人剛好被淘汰掉時,就會做出不結婚的決定,則會有 37 %的機率會孤老一生!這個結果顯然不合情理。而為了提高選中最好的對象的機率,並降低孤老終生的狀況發生,現代的社會也慢慢地接受了再婚、第二春。
所以我們將條件增加一個「可以離婚一次」。為了避免重複上方計算過的運算結果,也就是沒有離婚的情況,增加條件後,計算過程內先單純考慮離婚一次再遇到最好的機率。也就是說,在選中最好的對象前,我們可以先選一位跟他交往,之後仍然可以繼續相親,並且有權可以捨棄現在的對象,並和另一位交往,但這僅限一次且之後的條件就和原本一樣,不可反悔、不可回頭重新選擇。這裡我們先單純考慮一定需要離婚的情況,再加上不離婚的情況(上方的結果),即為所求。
首先我們同樣假定最好的人在 100 個對象中的第p位,然後必須在遇到最好的人p之前,先選到第1位到第p位內第二好的人,如此才能在離婚一次的狀態下選到最好的p,我們先稱之為局部第二好。而這個局部第二好,其實也就是前面所說的「第1位到第p−1位內最好的人」。
假設局部第二好是在100個對象中的第q位,而q為p−1中最好的機率為 1/p-1 。為了達到「離婚一次」的情況發生,q必須介在 x 和 p 之間,且在遇到 q 之前,第1位到第 x 位內最好的人(1到 q 中局部的第二好),就必須介在第1到第 x 間(淘汰期內),被當成選出q的標準,並被我們淘汰掉。如此一來,就能在x後,準確地選中局部第二好的對象(q),並發生離婚一次的情況,然後再選中最好的對象(p)。
故以 x , p, q 為變數, p為最好、q為局部第二好且選中p之機率函數為:
此時有p>q>x。
當固定淘汰x人後,且考慮q(局部第二好的人)的位置。當 q 在淘汰期內或 p 之後,發生離婚且再婚選中最好的機率為0(q會被淘汰或沒有發生離婚的情況),故q=x+1一直到q=p−1的時候,選到最好的對象在p的位置上的機率就是:
當固定淘汰x人後,且考慮完q的位置,再考慮p的位置。當p在淘汰期內或p在淘汰期後的第一位,發生離婚且再婚選中最好的機率為0 (會被淘汰或沒有發生離婚的情況),故p=x+2一直到p=100的時候,選到最好的人機率就是:
此時亦有:
這裡為必離一次婚的機率,故總機率F(X)為不離婚與離一次婚的總和,即:F(x)=f1(x)+f2(x)
此時欲有:
此時欲求F(x)的最大值,即找使得F(x+1)−F(x)<0且x為最小值:
假設:
最後簡化得算式:
把 K 代入數字運算,得到x為 24 時,K為<2的最大值。有最大的機會在可以離婚的情況下選到最好的對象。
經過我們的計算,發現x為24時,f1(24)≈0.3463406、f2≈0.2460007,也就是說有離婚一次的機會,在一樣的(淘汰期)為 24 時,為我們增加了約 24 %的成功率,使我們最大的機率有約 59.243 %的成功率,也就是說我們將前 24 個淘汰做為標準,則我們就會有接近六成的機率選到最好的對象。
至此因為我們利用了數學算出了最佳停止的時刻,而且加了可以接受離婚一次的條件,不但可以縮短淘汰期減少淘汰掉最好對象的可能,也減少了淘汰最好對象的機會(孤老一生的機會降低),所以使得成功率增加了不少,顯然這個結果是更好的。
人生中其實做這種不可後悔的決定是很常見的,除了結婚之外,諸如工作、學業,甚至於今天晚上吃什麼,許多時候總是做著這樣子不可後悔的決定。在做決定的時候我們除了憑自己的第六感之外,其實動筆計算一下,運用我們所學過的數學技巧,可以幫助我們能夠更好的擬定策略。如此看來,除了前六感外,若人生中多了數感做為第七感,似乎就可以做出最好的決定,也避免與完美情人擦身而過!可以過得更加愉快呢!