「痛、很痛、超級痛!」你有多痛?疼痛有客觀標準嗎?哪些因素會影響疼痛感受?——《痛:牛津非常短講》
測量疼痛 疼痛程度能被客觀測量嗎?
在二十世紀的前半,設計來檢測人類痛覺的機制主要是呼應從純粹身體觀點量測痛覺組成的需求。痛的主觀特質(或更直接地稱為由受測者本人提供的證據)若是遭到忽視還算最好的情況,在最糟的情況下甚至會遭到貶抑。疼痛程度應該要可以客觀量測出來,或說這就是大家進行相關研究的基本依據;一個人感受自己疼痛的方式與個性、道德觀,或甚至性別及種族有關。
再加上醫學的主要功能就是要檢測出傷病並尋求醫治的這種想法持久不衰,疼痛便成為次要的關注重點,只被視為反映出「眞正」問題的指標。疼痛的測量及客觀性因此被刻意保持著疏離、冷淡的狀態,與其說是缺乏同情的立論基礎,還不如說是完全置身於同情的範疇之外。
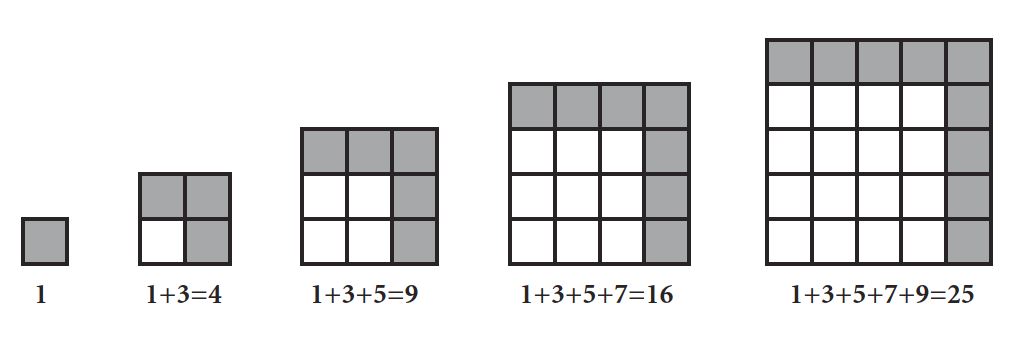
醫學的主要功能就是要檢測出傷病並尋求醫治的這種想法持久不衰,疼痛便成為次要的關注重點。pixabay
研究者主要想建立的是痛覺敏感度指數。他們希望知道人體的疼痛要到什麼程度才可以被偵測出來。一般而言,在受控的條件下,不同的疼痛程度顯然可以反映出受試者的文明程度、犯罪傾向,又或者相對「野蠻」的狀態。大家一直都知道,每個人的疼痛閾値——痛無法再被忍受下去的臨界點——差異甚大,不過痛在每個人身上可以被感受出來的最低程度是否具有根本性差異仍是重要議題。
痛的現代史是建立在主張特定「種類」的人不是對痛的刺激更為敏感、就是更難以忍受疼痛的研究之上。這對尋求專業醫療協助的疼痛患者造成了實質上嚴重的後果。他們獲得治療的程度——包括施加的麻醉劑劑量和醫護人員提供的同情心——可能都會跟種族、年紀和性別直接相關。
疼痛敏感度能成為犯罪證據?忽視痛覺主觀性,能幫助醫生更精準診斷嗎?
相當令人感到奇怪的是,生產可以測量疼痛敏感度的設備——痛覺計(algometer)或測痛儀(dolorimeter)——是心理學家和生理學家範疇內的工作。龍勃羅梭(一八三五─一九○九)因為在著作《犯罪人》(一八七六)中提出了犯罪類型分類而聞名,他採用了德國生理學家杜布瓦-雷蒙(一八一八-一八九六)開發的設備,透過電流刺激測量個體的疼痛敏感度及疼痛閾値。根據他的結論,成為罪犯的人對痛覺的「感受度較不敏銳,有時甚至完全感受不到」。而疼痛測量儀的數據就可以提供證據。
龍勃羅梭認為成為罪犯的人對痛覺的「感受度較不敏銳,有時甚至完全感受不到」。stocksnap
龍勃羅梭的研究是基於犯罪特質可以透過遺傳而來的理論,而且強調相關跡象都可以在人體上發現。他決心要透過比較(無論死活的)罪犯以及非罪犯之間的特質來證明這項理論,而獲得的結果非常驚人、具有高度影響力,但卻又毫無根據可言。不過他的例子可以反映出當時更為廣泛的趨勢。痛覺測量在機械領域的推進讓心理學家不再推敲心靈方面的非物質性運作,而改為追求物質性且具體可測的皮膚敏感度,並藉此探討大腦處理痛覺的各種相關能力(跟心靈完全不同的領域)。
另外在一九四○年的紐約醫院進行了一個計畫,他們將一盞燈的熱度聚焦在患者皮膚的一塊區域,然後記錄患者會開始感到疼痛的溫度,以及此疼痛到什麼程度會變得無法忍受。這是想將痛覺變成客觀可測量性質的一項新嘗試,其中帶有兩層意涵。
首先,痛覺若是可以被精準地測量出來,或許就能更有效地治療疼痛。其次,如果痛覺可以被測量,醫療體系就能更精準地評估患者對痛覺的反應(或可以無視哪些反應)。擁有機械測量的痛覺數據可以幫助臨床醫生超越(或甚至消滅)痛覺帶有各種隱喻且不甚精確的主觀性質。有些人就是會喜歡高報或低報自己受苦的程度,而這類傾向可以不再對醫療體系處理疼痛的藥物造成影響。
痛覺若是可以被精準地測量出來,或許就能更有效地治療疼痛。其次,如果痛覺可以被測量,醫療體系就能更精準地評估患者對痛覺的反應(或可以無視哪些反應)。stocksnap
可是問題在於這個痛覺量測系統不管用,至少任何一個實驗室的結果都無法在其他實驗室複製出來,因為受測對象可以在受過訓練後忍受不同程度的疼痛。外界刺激在受控條件下首先被人感知到的數値至少算是有找到共同的範圍,但疼痛閾値卻因為各種理由而出現各式各樣的差異,更何況個體實在很少(甚至不知道是否可能有)處於不受任何外在條件影響的「中性」狀態。
各種機械理論 人類的所有特質、體驗都能被測量及量化?
如果說與疼痛相關的機械性研究大多得算是笛卡兒的功勞,那是因為他被認定說過一些話,而那些話又顯然能讓後人從中發現一種透過「疼痛路徑」運作的特定機制。若是遵循這樣的笛卡兒觀點,人類這架機器被認定內建一個特定的痛覺系統,此系統將皮膚的神經末梢連結到脊椎,再連結到大腦中的「痛覺中心」。十九世紀以降的生理學家在勤奮不懈的努力下開始尋找特定的痛覺接收神經,或說所謂的「傷害感受器」(nociceptor)。
人類這架機器被認定內建一個特定的痛覺系統,此系統將皮膚的神經末梢連結到脊椎,再連結到大腦中的「痛覺中心」。pexels
他們認定所有形式的人類特質及體驗都可以被測量及量化,於是透過大腦秤重的數據建立起以種族、性別為指標的智商系統、透過頭骨的測量顯示文明化的程度,甚至利用各種精良的技巧拍攝臉部後描繪出「犯罪可能性等級」。另外還有一些「疼痛纖維」(pain fibres)被描述成跟特定種類的疼痛有關、又或者跟不同規模的疼痛有關。根據這種方式,大腦只是用來接受特定疼痛輸入訊號的接收器。於是自一九六○年代以來,疼痛量表等級可能跟傷勢程度呈正相關的基本前提已被確信是明顯錯誤的想法。
將疼痛以機械性解釋有哪些侷限?
沒有被這種機械性簡化手段抹消並在當代神經科學中獲得進一步探究的部分,是科學家依據刺激的種類及程度,將受激發的不同神經末梢做出分類。我們現在知道,人的體驗和神經刺激之間沒有絕對的相關性。雖然我們還是會用「傷害感受器」這個詞,但它們發出的訊號在成為痛覺前必須先通過大腦的解讀。機械性簡化看法的另一個問題在於,儘管這種說法用來描述一個人將腳放進火堆的情況看似合適,卻無法解釋那些無視特定神經損傷或直接刺激程度而出現的疼痛。於是又有更進一步的機械性解釋來試圖解決這個謎團。
為了解釋跟初始神經刺激不成比例的巨大疼痛反應,一八八○到一九五○年代出現了各種「(痛覺刺激及反應)模式」理論。有人假設一定是在脊髓中發生了某種反應,而且這個由原本末梢神經接收刺激所啟動的反應可以自我維持或甚至自我加強。隨著神經系統機制愈來愈常使用電機工程學的語言來比喻(而且使用的程度驚人),人們開始可以想像神經元在脊髓的「線路」中產生「反饋迴路」,因而「引起共振」並激發鄰近的其他神經元。正如原本那幅插圖所暗示,這種神經啟動的模式可以永無休止地延續下去,就算接受過治療或甚至原初起因已消失也沒關係(例如幻肢痛)。
機械性簡化看法的另一個問題在於,儘管這種說法用來描述一個人將腳放進火堆的情況看似合適,卻無法解釋那些無視特定神經損傷或直接刺激程度而出現的疼痛。於是又有更進一步的機械性解釋來試圖解決這個謎團。pexels
這個觀點的問題在於,這種帶有反饋迴路的電路板比喻想像起來容易,眞正要在實驗中發現卻有其難度。同樣地,疼痛方面的病變一直以來都被想像成一個「正常」的疼痛「電路系統」出現問題的結果,若要類比,就像是有訊號在特定種類的疼痛纖維中受到增強。在當代神經科學及疼痛管理領域中,這些理論的許多元素後來都證明在建構更全面性的疼痛體驗理論時很有幫助,但同時也必須超越「刺激帶來體驗」這種純然的機械性關係。
機械性關係以外的其他觀點?
直到一九六○年代,科學機構內外才開始出現批評的聲音——最有名的批評者是孔恩(一九二二-一九九六)和之後的拉圖(一九四七-)——這些人指出社會脈絡在科學工作中所扮演的重要角色,以及埋藏在社會脈絡中的各種想法及預設。到了更近期,達斯頓和蓋里森在他們的著作《客觀性》(二○○七)中重建了「客觀性」的概念。現在,所謂的「事實」已會被許多人視為透過特定框架後建構而來的偏頗資訊。這種不確定性為相關研究開展了全新的寬敞大道,但眞正的改變卻很慢才出現。
早在一八九四年,美國心理學家馬歇爾(一八五二-一九二七)曾有力地指出,快樂和痛苦都是心理狀態的不同特質;兩者是與情緒、感官、心靈和身體相連的「意識元素」,不過就在目睹摩根生產出行為主義式「定律」的這一年,這種全面性的思考觀點卻幾乎沒產生什麼漣漪。當痛的研究在一九七○年代確實開啟了痛覺的情緒及社會組成的相關探討之際,在醫療實務上對於能夠確切測量、判斷並診斷的既存需求,卻讓痛覺和傷害之間的機械關係得以續命。
馬歇爾曾有力地指出,快樂和痛苦都是心理狀態的不同特質;兩者是與情緒、感官、心靈和身體相連的「意識元素」。pexels
傷害的意象 第一份讓患者掌握自身疼痛體驗內涵的醫療評估問卷?
臨床醫生數十年來都帶著對痛的多面向理解在實務現場工作。梅爾扎克(一九二九-)和托格森(一九二四-一九九九)在一九七一年開發出了麥吉爾疼痛問卷。那是為了讓患者足以掌握自身疼痛體驗內涵的第一個精密醫療評估工具。疼痛問卷將痛的形容詞及比喻根據痛的強度進行分組,然後依照「感覺」、「情感」、「評價」和「其他相關」四種項目進行分類,再搭配圖表指出身體上的疼痛位置,另外還會針對其他症狀及一般生活方式進行整體評估。
此問卷的前提在許多案例中獲得證實,也就是受疼痛所苦之人會用類似的詞彙來描述特定的疼痛症候群。因此,疼痛問卷帶來的質化觀點對臨床醫療人員很有幫助,能讓他們在一開始更有機會根據患者對自身疼痛狀況的評估做出正確診斷。
梅爾扎克和托格森在一九七一年開發出了麥吉爾疼痛問卷。那是為了讓患者足以掌握自身疼痛體驗內涵的第一個精密醫療評估工具。stocksnap
當言語無法精準描述,我們如何形容疼痛感受?
乍看之下,這是將疼痛體驗的情感特質重新導入醫療體系的成功應對方式,並因此讓臨床評估朝新的方向前進,但這種做法還是有其限制。疼痛問卷被翻譯成許多其他語言時使用了同樣的武器修辭,或說同樣有關受傷、割傷、刺傷、射傷、揍傷或壓傷的各種比喻。許多學者都指出,這些用來描述人類疼痛體驗的比喻被使用的時間久得驚人,彷彿我們沒有足以訴說疼痛的直接用詞,所以非得求助於這些傷害意象。
不過,這種顯而易見的限制掩蓋了存在於人們陳述中的驚人豐富性及深度。隨著時間過去,武器的種類當然改變了,描述武器對人類造成的傷害種類也出現了更多具有想像力的比喻性說法。此外,隨著語言的改變,人們會發現無論是問卷中的表達方式、代表意義及所處脈絡,都具有難以將其中分類普遍化的細微差異。翻譯的政治(更別說是做法)總是會引發誰的用語足以建立起基本分類架構的疑慮:我們應該要採用患者、醫生,還是譯者的用語?
為了聽見疼痛的主觀陳述而定下語言框架的嘗試,反而造成了將痛客觀化的效應。pexels
一旦語言被認定為一個人描述主觀體驗的重要資訊載體,我們就很難將其限制在事先規範好的定義及分類中。疼痛問卷成功地將許多當時在英文中常用的疼痛描述整理在一起,不過也可能限縮了人們在未來描述疼痛的用詞。當醫療人員把一連串描述性用詞交給患者並要求他們找出「符合」自身痛感的詞彙時,這種做法很可能會被視為一種具有高度暗示性及影響力的策略,因為這份用詞淸單暗示了這些詞彙已捕捉到了疼痛的本質。
這種做法對某些人來說可能有用,但有些人即便感覺不太對勁,仍得努力將這些用詞硬套到自身的感受上。另外還有些人在覺得這些用詞完全無法用來描述自己的狀況時,甚至會開始質疑自己的疼痛是否眞實存在。為了聽見疼痛的主觀陳述而定下語言框架的嘗試,反而造成了將痛客觀化的效應。
說到底,一九七○和八○年代在尋求痛的情感特質時,是放入由固定價値觀所掌控的基模(schema)中,就像身體的疼痛値也是由機械主導的客觀數値來決定。患者的聲音並不是沒被聽見,但也受到既有的量測方式取代。
受教育程度會影響疼痛體驗嗎?疼痛分類因文化不同有所差異?
根據一份由哈里森所進行的研究指出,當麥吉爾疼痛問卷在科威特被翻譯成阿拉伯文時,編纂者非常淸楚意識到,即便是在當地社群內部也出現了溝通上的語言偏差。受過教育的科威特人因為懂英文而擁有較多字彙量,因此可用「對一般患者而言過於深奧」的詞彙來描述他們的痛覺。難道這代表他們的疼痛體驗也就因此有所不同嗎?我們很可能永遠不會知道,因為這類描述被有意識地迴避掉了。
有意思的是,阿拉伯文譯者也迴避了對慢性疼痛患者伸出援手,因為「他們的痛覺評分標準跟那些……經歷急性疼痛的人相比有系統性的不同」。如果有人記得的話,麥吉爾疼痛問卷一開始的設計是要嘗試深入理解疼痛症候群的疼痛體驗——也就是完全以受到慢性疼痛所苦的人為目標——因此我們可以認定這個翻譯策略反而阻礙了這項量測工具原本的概念性目標。
受過教育的科威特人因為懂英文而擁有較多字彙量,因此可用「對一般患者而言過於深奧」的詞彙來描述他們的痛覺。難道這代表他們的疼痛體驗也就因此有所不同嗎?unsplash
二十世紀醫學對於調查對象必須在各項數値方面完全中立的需求,阻礙了我們去探索疼痛體驗中的一項核心元素,因為那個核心元素本身就是作為一種情感的主觀値。疼痛情感的語言表述——人們針對自身感受說出的話——本身抗拒任何精確的製表及分類作為。科威特的那些譯者對此擁有第一手體驗,他們發現原本在英文中被歸類為「感覺」的詞彙,在翻譯後更接近「情感」或「評價」的類別。
這些作者後來做出結論,「我們有很充足的理由認定,疼痛分類會因為不同文化而有所差異。」比如他們就找不出翻譯「射傷」(shooting)這種痛覺的詞彙。在此同時,義大利文把「射傷」這種痛覺翻譯成「像是床墊彈簧反彈」的痛。
整體而言,根據二○○九年由雪梨的喬治國際健康研究所做的研究,麥吉爾疼痛問卷被翻譯成了二十六種語言,研究發現這些翻譯後的問卷效力普遍不佳,並建議必須謹愼使用這些「非英語版本」的問卷。這些不同版本的問卷中描述疼痛的詞彙從四十二到一百七十六個不等,反映出了人類口中疼痛體驗的豐富程度。這些疼痛反抗或拒絕被分類列表的特質只顯示了人們不是(或說至少不完全是)機器。
——本文摘自《 痛 :牛津非常短講 012 》,2024 年 02 月,左岸 文化 出版,未經同意請勿轉載。




























0GGK0374_痛:牛津非常短講012_立體_300dpi.jpg)