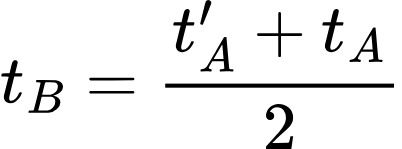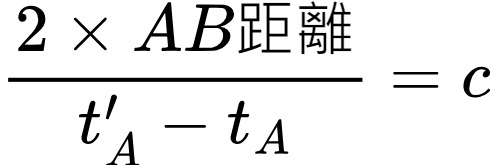- 文/賴昭正 前清大化學系教授、系主任、所長;合創科學月刊
你聽過「雙胞胎悖論」嗎?
我有時會問自己,我是如何發展相對論的。我認為其原因是:一個正常的成年人從不去思考空間和時間的問題——這些都是他小時候就想到的;但我的智力發育遲緩,因此長大後才開始思考空間和時間。
——愛因斯坦(Albert Einstein)),1921年諾貝爾物理獎得主
1905 年,愛因斯坦在題為「關於運動物體之電動力學」的論文裡,從兩個簡單的假設,得到結論謂如果張三與李四相對運動,則張三會認為李四的手錶跑得比較慢。在證明這一稱為「時間膨脹」(time dilation)的現象後,寫道:
由此產生以下奇怪結果。如果(開始時)A 點和 B 點在(靜止坐標)K 中觀察是同步的(即同一時刻),但 A 處的時鐘以速度 v 沿 AB 線到 B,則在到達 B 時,兩個時鐘將不再是同步:移動到 B 後的 A 時鐘將落後於保持不動的 B 時鐘…。我們得出這樣的結論:如果兩個 A 處同步的時鐘,其中一個以恆定速度沿閉合曲線移動 t 秒後返回 A 處,則保持靜止的時鐘將發現剛返回的時鐘慢了 tv2/(2c2)秒(c 為光速)。

或許是怕像筆者這樣智力發育遲緩的讀者難懂,愛因斯坦於 1911 年重申並詳細說明這一現象如下:
如果我們把一個活的有機體放在一個盒子裡……我們可以安排這個有機體在經過任意長時間的飛行後,在幾乎沒有改變的情況下返回到它原來的位置。此時保持在原來位置的相應有機體已經早已讓位於新一代,但對於移動的有機體來說,只要運動以接近光速進行,漫長的旅程只是一瞬間而已。
名物理教科書作者雷斯尼克(Robert Resnick)更清楚地解讀謂:
如果靜止的有機體是一個人,而旅行的是他的雙胞胎,那麼旅行者回到家時會發現他的雙胞胎兄弟比自己老得多。但在相對論中,任何一個雙胞胎都可以將另一個視為旅行者,因此再碰面時將比他自己年輕。這在邏輯上看來是一個矛盾的現象,因此被稱為「雙胞胎悖論」(twin paradox)。
「雙胞胎悖論」可以說是相對論中最著名的想像實驗,為許多教科書與通俗科學文章所討論的對象;但筆者卻發現在「泛科學」裡只有一篇書評的文章中提到它!
難道真如諾貝爾獎得主普朗克(Max Planck)所說的:「一個新的科學真理之所以勝利,不是因為說服了它的對手,讓他們看到了光明,而是因為它的對手最終會死去,而熟悉它的新一代會成長起來」?在習以為常的熏陶下,現在的「新一代」已經不再認為「雙胞胎悖論」是值得討論的悖論?
如果你不是這樣的「新一代」,那本文是為你所寫的,相信你在這裡將讀到在其它地方找不到之「雙胞胎悖論」的白話文解讀(不用任何數學)。
同步與同時的「相對性」
普朗克謂:「光速之於相對論就像基本的作用量子之於量子論:光速是相對論的絕對核心。」
可是如何測量光速呢?從甲處發一道光到乙處,將甲乙之距離除以光旅行的時間就得到光速。當然,要能精確地測得光速,甲乙兩處的時鐘必須是互相校正過的、同步(synchronized)的。如何校正甲乙的時鐘呢?相信很多人小時候就已經知道了:將兩個時鐘帶到同一處,然後像電影中之突擊隊,在出發前由隊長發命令說:「讓我們校正時間,現在是……」 。
可是愛因斯坦不知道為什麼竟然沒有想到這一點?或許真的是「智力發育遲緩」,他竟然建議在乙處放一面鏡子來反射甲處在零時刻所發的光,如果乙處接到光的時刻正是甲處光來回所需之時間的一半,我們便說甲乙兩處的時鐘同步化了。用這種方法來同步化時鐘,很顯然在邏輯上我們便不可能測單方向的光速是否為定值了,所以愛因斯坦增加了一個假設,即光是在真空中的傳播速率為一與發射體運動狀態無關的定值 c!
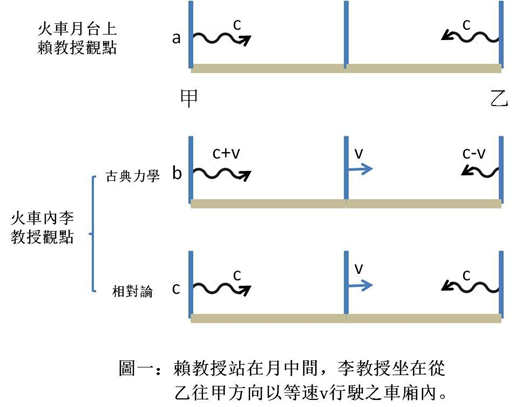
如果我們將同步化的甲乙兩個時鐘分別放在火車月台的兩端,讓它們在同一時刻(零點)往月台中心發射一道激光,則站在月台中心的賴教授應該「同時」收到來自甲乙兩端的激光(圖一 a)。
但坐在從乙往甲方向以等速 v 行駛之車廂內的李教授,卻發現甲、乙激光發射後一直在以同一速度 c 逼近賴教授(圖一 c);但因賴教授在往乙方向運動,因此如果光同時到達賴教授處(任何人都同意的「事件」,否則賴教授不是說謊就是頭腦有問題),李教授將下結論謂:甲乙兩個時鐘並不同步,甲時鐘顯然先發射,因此比乙時鐘快(甲的零點比乙的零點早)!
所以「同時」將因觀察者之運動而異:賴教授說甲乙兩激光是同時發射的,李教授卻說甲激光先發射的!如果李教授坐的火車是由甲往乙方向行駛呢?他將發現乙激光是先發射的!
這似乎是很明顯的結論,為什麼要等愛因斯坦告訴我們、難道牛頓沒想到嗎?牛頓不是沒想到,而是他認為宇宙中有一獨立於任何觀察者的時鐘,稱為「絕對時間」,所以「同時」是絕對,不會因觀察者之相對運動而異。
但事實上這結論與絕對時間無關,而是因愛因斯坦之假設—光的傳播速率為一與發射體運動狀態無關的定值—造成的!如果不是這一假設,則光的傳播速率將與發射體運動狀態有關(古典力學),李教授會認為乙激光是以 c-v 逼近、而甲激光則是以 c+v 追趕以 v 速運動的賴教授(圖一 b),因此兩道激光當然還是同時到達賴教授處!所以李教授和賴教授都同意時鐘是同步的。
所以很明顯地應是愛因斯坦的「同時相對性」改變了人類根深蒂固的「絕對同時性」觀念。如果我們將「發射激光」改成孿生子(雙胞胎)的「生日慶典」,則賴教授將說他們是同時出生的;但是李教授則會因其運動狀態而說甲孿生子先出生(比較老)或乙孿生子先出生。這不正是「雙胞胎悖論」的一個影本嗎?我們在這裡事實上還看到一個很重要的現象:參考坐標(運動方向)的改變,可能顛倒兩個不同事件的「先後次序」!
雙胞胎悖論
假設雙胞胎張四決定乘坐等速高速太空船去旅行。因他決定一去不回,故在旅行前與張三痛哭擁抱,答應在死前一刻依自己的時鐘將年齡紀錄下來,「寄」回地球。
依照經驗,如果兩人的生理機能完全不受外界的影響,則兩人的壽命應該一樣長;但是依照相對論,張三認為張四是在運動,其(生理)時鐘跑得較慢【稱為「時間膨脹」現象】,因此活得較長;同樣地,張四認為張三是在運動,其(生理)時鐘跑得較慢,因此活得較長!誰對呢?智力發育遲緩的筆者認為這是矛盾的,一定有一個人錯,但愛因斯坦說兩人都沒錯,要筆者耐心地等一等……。

歲月如梭,張四的信終於抵達地球了;打開一看,怎麼?他的壽命竟然與張三一樣!筆者一個頭兩個大,顯然是不應該學物理—尤其是相對論!請讀者幫幫忙吧!
假設張四離開10年(他的時間)時突然想家,於是緊急剎車,將太空船轉個方向,緊急加速到原來的速度(為了方便,我們可以假設整個過程是「瞬間」),10 年後終於又回到地球,跟雙胞胎張三重新會合,正要擁抱時卻發現張三已經比他老多了!這正是上面愛因斯坦及雷斯尼克所說的結果。
這看似矛盾的結果事實上是很容易理解的:張四在太空中的「緊急剎車、將太空船轉個方向、緊急加速到原來的速度」破壞了兩人運動的對稱性。我們雖然沒有辦法感受到自己是在靜止狀態或者是在等速運動,但我們卻可以知道自己是在加速。所以張四在太空中的急轉彎,不但破壞了兩人運動的對稱性,也應該是造成他們年齡差異的原因。我們可以從兩方面來看為什麼改變速度(加速)造成年齡差異。
從相對論來看,在去程及回程的等速運動時,張四應該一直認為張三比他年輕。但在前面的火車站實驗中,我們發現李教授的火車行駛方向改變會造成「先後次序」的顛倒,因此張四在太空急(「瞬間」)轉彎的過程中會發現張三(「瞬間」)老了許多(不怕數學讀者,可參見附錄二):多得超過了剛提到之等速運動時的年輕數,因此張四在相會時將發現張三比他老!從張三的角度來看,他從未加速,因此認為在運動的張四一直比他年輕!不止如此,他依相對論所算出來的年齡差距,也正是張四依他自己之坐標(包括等速與改速)所算出來的!
相信某些讀者要問:「老」是生理現象,張四的坐標轉換怎麼會使張三變老呢?火車站實驗中的「先後次序」顛倒,只是李教授的觀點而已,並沒有實質的物理意義,賴教授不是不同意嗎?1905年的相對論沒有回答這個問題,這答案 10 年後才在廣義相對論中出現(詳見愛因斯坦一生中最幸運的靈感-廣義相對論的助產士):加速可以視為是一種重力現象,時間在重力場中跑得比較慢【稱為「重力時間膨脹」(gravitational time dilation)】。
所以張四在太空中急速的減速及加速將造成強大的重力場,使得其(生理)時鐘變得非常慢,因此在這期間老得也非常慢(在黑洞附近的人—如果不被吸進去的話—幾乎可以長生不老)!

長度收縮
特殊相對論還預測一個稱為「長度收縮」(length contraction)的怪現象,謂:一位快跑健將拿著一根棍子沿著棍子方向以速度v飛跑,旁觀人會認為棍子長度變短。這一個怪現象事實上在月台的實驗上已經看到了:要決定兩點之間的距離,我們必須「同時」測兩點的坐標;李教授認為甲的零點比乙的零點早,因此必須「稍等」甲一下才能「同時」記錄甲、乙兩點的坐標,但這一「稍等」,因為甲在往乙方向運動,不是使得測得的距離變短嗎註?
如果讀者不怕數學,讓我們在這裡用點數學來看「長度收縮」這一怪現象,希望能幫助讀者更進一步了解。
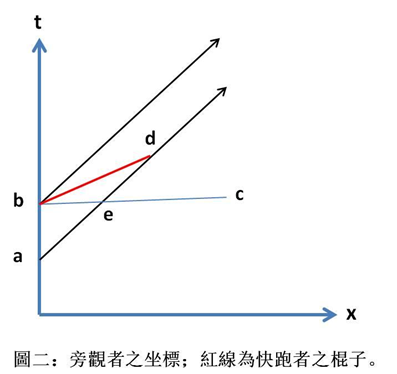
圖二是旁觀者的坐標,顯示在 t=a 時,棍子的前端進入原點 x=0,然後沿軌跡 x=v(t-a) 繼續前進;棍子的後端則在 t=b 時進入原點,然後沿軌跡 x=v(t-b) 繼續前進。
圖二中的 bc 是棍子後端剛進入原點時,旁觀者的「同時」線,即線上每一點的時間都是 t=b(同步化)。測量棍子的長度必須「同時」觀察其前端及後端的位置,因此他測量得到的棍子長度為 be(他不知道那個時刻棍子前端事實上已經到達 d 點了)!bd 是快跑健將的同時線,其 x 坐標 (xd-xb) 則是 他測量的棍子長度,比 be 長;所以旁觀者說「棍子變短了」。
如果快跑健將的速度不快,則前、後端軌跡將趨近於成垂直,不同運動狀態的「同時」便趨近於相同,我們便又回到我們所熟知的牛頓世界了!

結論
愛因斯坦1905年的相對論中之「光傳播速率為一與發射體運動狀態無關的定值」假設徹底地毀滅了物理學中「同時」的觀念,因之產生了一些與日常經驗不符的奇怪現象,如「長度收縮」及著名的「雙胞胎悖論」。
希望本文的解釋不但能讓讀者見怪不怪,甚至發現其實不怪;了解相對論裡所有「矛盾」現象都是因為不同觀察者在「自說自話」造成的:例如在棍子的例子裡,靜止觀察者談論的是他(靜止觀察者)在某個時刻測量得到的長度,而移動觀察者談論的則是他自己(移動觀察者)在另一個瞬間測量的長度。
時間及空間是人類製造出來便利溝通的語言,如果李教授不認為甲地先發射,他沒辦法解釋為什麼賴教授同時看到甲乙兩地發射出來的光(實際經驗到的物理現象);所以「自說自話」原來是為了保持物理定律的不變性(物理定律是用來解釋我們實際經驗到的物理現象)。這些「自說自話」事實上也不是隨便說的,而是靠「洛倫茲轉換」(Lorentz transformation)連接在一起的。
附錄一:「後見之明」輕鬆地推導「洛倫茲(坐標)轉換」公式
K’ 坐標以 + v 速度相對於 K 坐標運動。如果坐標在 t=0 時重合,加上時、空的均勻性(變數沒有二次方):
…………………………………………………………(1)
β 為待解的常數。如果在 t=0 時發射一道光,則光的軌跡為 x=ct;代入上式,得
…………………………………………………………(2)
因為 K’ 坐標及 K 坐標的對稱性:
…………………………………………………………(3)
將 (3) 代入 (2) 解得
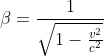
從 x = β ( x’ + vt’ ) 解 x’ ,然後代入(1),化簡可得到
…………………………………………………………(5)
公式(1) 、(5), 及(4)就是「洛倫茲(坐標)轉換」公式。長度收縮中之快跑健將棍子的同時線方程式為公式(5) :
附錄二:雙胞胎悖論的數學
假設雙胞胎甲留在地球,雙胞胎乙決定以 v 速度往太空地球 S 旅遊,則甲(x , t)、乙( x’ , t’)兩人的坐標轉換為(為了方便,將光速定為 1,所以 v 應該小於 1 ):
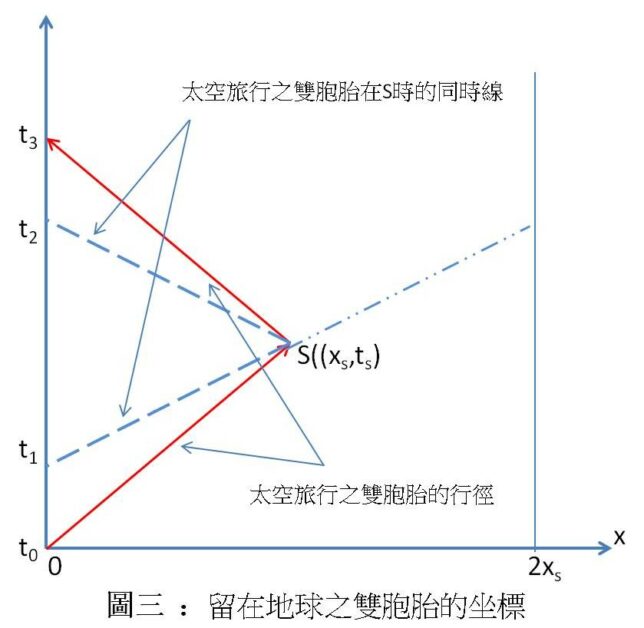
圖三為甲的坐標圖:太空地球 S 的位置為( xs , ts)。依照上面公式轉換,對乙來說,其坐標為( x’s , t’s )。去程時,乙在 S 時的同時線(該線上每一點的時鐘都「同步」) t1s 為:
在到達 S 時,乙瞬間改變方向,其同時線瞬間變為 t2s :
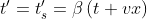
這兩個方程式的時間零點分別為 t0 及 t3 ,因此不能直接用它們來算去程及回程的同時點 t1 及 t2 ;但因為對稱的關係,我們可以將 t1s 延長到 x=2xs 處,用 t’s=β ( t-vx ) 解得:
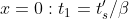
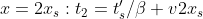
所以乙的回程坐標轉換一下子讓甲老了
t2 – t1 = v2xs
……舉個實際的例子:如果 v=0.6, xs=6,則 β=1.25,所以對甲來說,乙需要 10(=6/0.6) 年才能到達 S ,也需要 10 年才能回來,因此乙回來時,甲應該已經 20 歲了(為了說明方便,假設他們一出生,乙就到太空旅行)。甲的 S 坐標為(6 , 10),透過坐標轉換,乙的 S 坐標為(0 , 8);所以甲認為乙的時鐘比較慢,只要花 8 年(乙時鐘)的時間就可以到達 S,同樣地也只要花 8 年時間回來,所以乙回來時應該只有 16 歲!
透過乙在 S 時的同時線,可以解得當 x=0 時,t1=6.4。所以對乙來說,他已經 8 歲了,但甲才 6.4 歲,顯然比他年輕(老得慢)!同樣地,在回程時,乙也應該認為他老了 8 歲,但甲才老了 6.4 歲,所以乙回到老家時,乙應該已經 16 歲,但甲才 12.8 歲,比他年輕!
但前面不是說過甲應該已經 20 歲了嗎?矛盾?不!我們忘了乙坐標轉換時的「時差」 :7.2 年!將這「時差」加進去,乙也計算出甲的年齡應該是 20 歲(=6.4+7.2+6.4)!
甲、乙兩個人的結論相同,沒有矛盾!愛因斯坦沒有騙我們!
註:
要決定兩點之間的距離,我們必須「同時」測兩點的坐標;同樣地,要決定兩個事件發生的時差(時間),我們必須在「同點」測兩個事件發生的時刻。相對論不但毀滅了物理學中「同時」的觀念,事實上也摧殘了「同點」的觀念:沒有絕對的空間,「同點」因運動者而異。所以我們也應該可以在類似月台的簡單實驗上尋找到「時間膨脹」的現象(請讀者幫幫忙吧)。
延伸閱讀
愛因斯坦一生中最幸運的靈感-廣義相對論的助產士(科學月刊,2021 年 5 月號)。