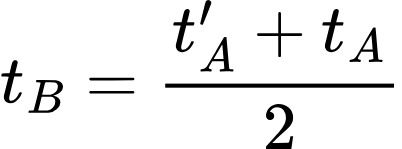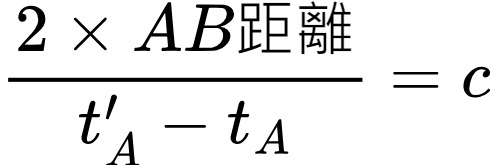「時空」
本書的目的是用最具有啟發性的方式來闡述時間和空間,我們認為過去在建立相對論時,所用的描述方式並不是最好的。現在距離愛因斯坦具有革命性的發現已經超過一個世紀了,從現代的觀點來看,我們發現了能更深入理解,並且更令人滿意的看待時間和空間的方式。我們決定不再對以往那些陳舊的教科書式的內容進行深挖,而是一切歸零,從頭開始。在這個過程中,我們將能夠慢慢理解閔考斯基所說的,時間和空間必須融合在一起,形成一個新的混合體。一旦我們對它們有了一個更加全面和合理的理解,將很快能夠達到我們最重要的目的,那就是依靠自己的力量推導出 E=mc2 這個公式,從而理解相對論的核心精神。
那麼,我們就從這兒開始吧。愛因斯坦的理論可以完全用幾何的方式表達出來。也就是說,你並不需要代數幫忙,只要靠圖形和概念就足夠了。這套理論中,存在著三個核心概念,即不變性、因果性和距離。除非你是個物理學家,不然前兩個概念對你來說也許很陌生。至於最後一個,也許你會認為自己對它很熟悉,但其實它也和你所想的不盡相同。
不變性是現代物理學中的一個核心概念。現在,請將你的目光從你眼前的書本上移開,抬頭看看你前方的世界。然後,請轉身向相反的方向看去。你的房間會因為你的視角不同而看起來不一樣,但是自然法則卻是不變的。不論你對著東南西北當中哪個方向,重力都還是一樣大,使你牢牢地站在地上。就算把電視調換個方向,它依然能正常運轉;而不論你把車子留在倫敦、洛杉磯還是東京,它都能發動;這些都是自然界中具有不變性的例子。若只是這樣的話,不變性看起來僅僅是陳述了一些顯而易見的事情,但如果將不變性延伸到我們的科學理論中,就會被證明是一項意義非凡的事。我們剛剛討論了兩種不同形式的不變性,一種叫作「旋轉不變性」,也就是當我們旋轉並且朝著不同方向測定自然法則時,它們保持不變。另一種叫作「平移不變性」,表示當我們從一個地點移動到另外一個地點,兩點上的自然法則保持不變。這兩條看似毫不起眼的法則,到了諾特這位曾被愛因斯坦稱為數學史上最重要的女性手裡,就變得異常強大。一九一八年諾特發表了一個定理,揭示了不變性與特定物理量守恆的深入關係。我們將對物理界中的守恆定律做更多的討論,但現在我們先直接使用諾特發現的這個關係。對於從不同的角度觀察世界這個實際例子來說,如果自然法則不因我們面對的方向不同而改變,那麼這當中便存在某種守恆的量。在這個例子中,守恆的是角動量。而對於那個有關平移的例子來說,守恆的是動量。不變性到底為什麼重要呢?讓我們揭開這個有趣的物理事實的神祕面紗,看看它的真面目。
月球以每年四公分的速度遠離地球。這是為什麼呢?首先請在你的腦海裡將月球想像成靜止懸掛在一個不停自轉的地球上空。月球直射下的海水會因為月球重力的影響而向上凸起一些,地球在此影響下以每天一周的速度自轉,這樣就形成了海水的潮汐。海水和地表之間存在著摩擦力,正因如此,地球自轉的速度不斷減慢。這個影響雖然很小,但也能被測定出來。每一地球日的長度在一個世紀的時間裡會增加大概千分之二秒。物理學家們都是透過角動量來測量旋轉的速率,所以我們可以說地球的角動量隨著時間推移不斷減少,也就是說地球的自轉速率在不斷減慢。而諾特告訴我們,世界從任何一個角度來看都是一樣的(更準確地說是,在旋轉的狀態下自然法則具有不變性),所以角動量是守恆的,也就是說所有轉動的總量是不會改變的。那麼地球因為潮汐現象產生的摩擦力導致自轉速度減慢,這當中所失去的角動量上哪兒去了呢?答案是,它們被傳遞給了月亮,使得它在環地球軌道中加速運動,以抵銷地球自轉慢慢減速的作用。這導致月亮移動到距離地球稍稍更遠的地方。換句話說,為了保證整個地月系統中角動量的守恆,月亮必須經由移動到一個更寬的環地軌道上,才能補償由於地球自轉減慢所帶來的影響。這是一個十分真實,也非常奇妙的現象。月亮是如此巨大,誰會想到它年復一年的漸行漸遠,都是為了角動量守恆。義大利小說家卡爾維諾被這個奇妙現象深深吸引,他創作出一個短篇故事,名為〈月亮的距離〉。在這個故事裡,作家想像在遠古的某個時候,我們的祖先每天晚上都能坐船穿越海洋到達月亮停靠的地方,並且用梯子就能爬到月球的表面。然而隨著月亮不斷地遠離地球,終於有一天晚上,那些喜歡月亮的人們必須面對一個選擇:永遠待在月亮上與世隔絕,或是永遠告別月亮返回地球。卡爾維諾筆下這個奇幻浪漫的故事,能在不變性這個抽象概念以及不變性與物理量守恆定律的深層關係中找到解釋。
在現代物理學中,用任何語言來描述不變性的重要都不過分。因為物理學界一直追求的便是建立一個知識體系,在這個統一的架構中,法則將是真理,不被質疑。作為物理學家,我希望發現宇宙的不變性是因為,正如諾特早就知道的那樣,這些發現將帶給我們真實確鑿的解釋。因為大自然的簡約之美通常隱藏在眾多表象之後,所以找出那些具有不變性的性質相當地困難。
沒有什麼比現代粒子物理學更能體現這一點。粒子物理學是研究次原子級微觀世界的一門學科,它也致力於尋找構成宇宙的最基本單位,以及將它們聚集在一起的自然之力。在前文中,我們已經接觸過基本力的一種,那便是電磁力。透過理解它,我們對光的本質有所了解,也讓我們開始走上探索相對論的道路。在次原子世界中,存在著另外兩種占有支配地位的自然之力。強核力將原子核聚集在原子的中心,弱核力則是星星能夠閃閃發亮的原因,同時還控制著某幾種放射性衰變,例如,以放射性碳定年法來確定物品的年代也得依靠弱核力。第四種力大概是我們最熟悉的萬有引力,同時它也是最弱的,遠不及其餘三種力。目前為止,愛因斯坦的廣義相對論依然是我們已知的關於萬有引力的理論中最準確的,如同我們在最後一章中將會看見的那樣,它是個有關時間和空間的理論。在這四種力的影響下,僅僅靠十二種基本粒子便構成了我們眼睛能看到的所有物體,包括太陽、月亮、星星,還有太陽系中所有行星,當然也包括我們的身體。起初看來幾乎是變化無窮的宇宙,這麼一說就變得難以置信地簡單起來。
朝窗外看看。也許,你在午後的陽光裡瞥見玻璃帷幕建築上整個城市變形的倒影,又或許你看見的是草原上整齊的欄杆裡黑白相間的乳牛。但不論是城市還是鄉村,從每一扇窗戶看出去,幾乎都能看見人類活動留下的痕跡。雖然人類文明無處不在,但二十一世紀的物理學告訴我們,這一切歸根結柢都只是由四種自然力掌握之下的極少數幾種次原子級粒子所跳的韻律操。一百三十七億年來,一直如此。構造複雜的人類大腦和我們看見的那些由意識和靈巧工藝交織而成的產物,展示了大自然潛在的簡單與優雅之美。科學家的任務則是搜尋這些羅塞塔石碑般的特質,使我們能破解自然的語言,並展示她的美。
尋找並運用這些特質時,我們所仰仗的工具是數學。就其本身而言,這是一門不斷湧現艱深問題且發人深省的學科。已經有大量的書籍花整本書的篇幅嘗試去解釋,為什麼數學這門學科是我們所知道的這樣。讓我們再次引用維格納的一段話:「在總結歸納物理法則的過程中,數學語言表現得幾乎天衣無縫,這是一種恩賜,我們無法理解,甚至不配探究。」或許我們終究無法理解數學和自然之間關係的本質,但歷史告訴我們,數學能夠幫助我們有效地梳理頭緒,並有效地指引我們加深認識和理解。
我們不斷強調並堅持的一點是,物理學家寫下很多公式,唯一的目的是表達真實世界中不同事物間的關係。「速度=距離/時間」這個公式便是一個例子,我們在上一章中討論光鐘的時候就碰到過,用數學符號表示則是 v = x/t,其中 v 代表速度,x 代表距離,t 代表走過 x 這段距離所需要的時間。所以我們非常容易得出,如果你在一小時中走了一百公里,那麼你的速度便是每小時一百公里。我們最感興趣的是那些能夠描述自然某方面的特性,同時又能讓所有人贊同的公式。也即是說,它們只包括那些具有不變性的量。這樣一來,我們便可以在所測量的物件上達成一致,而不受限於視角的不同。根據常識,我們知道空間中任意兩點間的最短距離是個不變數,至少在愛因斯坦時代之前是這樣。然而我們在上一章中看到,事實上卻不是如此。要牢記:常識並不總是可靠的。與之類似,時間的流逝已經變成了一個主觀的感受,它的快慢隨著時鐘之間相對速度的變化而改變。愛因斯坦把一切固有的觀念都弄亂了,我們甚至不能用距離和時間來建立一個較為準確的宇宙觀。從一個以找尋基礎自然法則為目的的科學家看來,v = x/t 這個公式從本質上來說沒有任何用處,因為它並不能表達不變數之間的關係。屏棄時間和空間的同時,我們動搖了物理學的根基。現在我們該怎麼辦呢?
(全文未完)
摘自《為什麼E=mc2?探索時空、質量之源與希格斯粒子》第四章〈時空〉。本書由貓頭鷹出版社出版,獲2012年12月PanSci選書推薦。