為什麼A4的紙張邊長比是根號2呢？──《數學好有事》

從簡單陳述句轉變為複合句——「連接詞」

大約一百年後，克律西波斯（c.280 – c.206 BC）改變了邏輯的關注焦點，從簡單的主述詞陳述句轉向「蘇格拉底是人，且芝諾也是人」之類的複合句。

這是很大的進展。當時甚至有人說「克律西波斯的邏輯就是神會用的邏輯」。我們稍後會見到，克律西波斯的邏輯也是人類使用的邏輯，只不過我們還得等兩千年才會明白這一點。

複合句使用的連接詞不同，其真假受個別句子影響的方式也不同。

譬如「不是…就是…」這個連接詞組可以這樣用，也只有「不是…就是…」這個連接詞組可以這樣用：

編按：「不是」穆罕默德到山那邊，「就是」山到穆罕默德這邊。

其後一千五百年甚至更久，克律西波斯沒有對邏輯留下多少影響。不僅因為他的作品失傳了，只留下他人的轉述，也因為亞里斯多德成了天主教會的心頭好。

萊布尼茲定律

接下來兩千年，邏輯學家建構出愈來愈多三段論，有些甚至前提不只兩個。這些邏輯學家就像煉金術士，拿著概念拼拼湊湊，想辦法生出有效論證。最後有一個人在這股狂熱當中想出了方法，那人就是萊布尼茲（1646 – 1716）。

萊布尼茲想到的方法是將陳述句看成代數裡的等式。等式使用等號（＝）來表達式子兩邊數值相等。

例如：x2 + y2 = z2

萊布尼茲將等號帶進邏輯裡，用來指稱 a 和 b 等同。

自此之後，這個等同式就叫做「萊布尼茲定律」。萊布尼茲將 a = b 拆成兩個不可分割的述句「a 是 b」和「b 是 a」，意思是「所有 a 都是 b」和「所有 b 都是 a」。

例如：「所有單身漢都是沒結婚的男人，且所有沒結婚的男人都是單身漢。」

若 a 和 b 等同，那麼陳述句裡的 a 就算換成 b，這個陳述句的真假顯然不會隨之改變。例如，「蘇格拉底是沒結婚的男人，沒結婚的男人是單身漢，因此蘇格拉底是單身漢」。

這個定律很重要，因為有了它，我們就能以有限多的步驟來判斷近乎無限多的句子的真值。萊布尼茲使用的步驟數是四個。

1. a = a

例：「蘇格拉底是蘇格拉底。」

2. 若 a 是 b，且 b 是 c，則 a 是 c

例：「所有人都會死，蘇格拉底是人，所以蘇格拉底會死。」

說「a 是 b」就等於說「所有 a 都是 b」。

3. a =非（非 a）

例：「如果蘇格拉底會死，則蘇格拉底不是不會死的。」

4. a 是 b = 非 b 是非 a

例：「蘇格拉底是人，意思是如果你不是人，你就不是蘇格拉底。」

利用這四個簡單的法則，萊布尼茲就能證明所有可能出現的三段論。比起亞里斯多德的四角對當，這才是人類史上第一個真正的真理理論，因為它使用事先定下的法則，藉由代換等同的符號（同義詞）來導出結論。

非真即假的歸謬法

萊布尼茲最常用的證明方法是一個極為重要的邏輯工具，深受後世邏輯學家和哲學家喜愛。他稱呼這個方法為歸謬法。

這個工具很簡單，卻好用得驚人，自萊布尼茲發明以來便廣獲使用。我們用一個例子來講最清楚。

使用歸謬法時，我們先假設要檢驗的那個陳述句為真，再看它能導出哪些結論。如果導出的結論互相矛盾，我們就知道那個陳述句是假的，因為矛盾永遠為假。

歸謬法有一大好處，那就是即使我們不知道如何證明，也能判斷一個陳述句的真假；只要證明這個陳述句的否定會導出矛盾，就知道它是真的了。

新工具

「我發明的這個工具完全使用理性，是裁決爭議的判官、解釋概念的權威、衡量可能性的天平、指引我們穿越經驗之海的指南針，是萬物的清單、思想的表格、檢視事物的顯微鏡、預測遙遠事物的望遠鏡、通用的演算法、不使詐的魔術、不空妄的計謀，也是人人都能用自己的語言閱讀，所及之處皆會帶來真宗教的經文。」

萊布尼茲致信漢諾威公爵，1679 年

不難想見，天主教會將萊布尼茲視為異端。但「思想有其必然法則」的想法卻對西方哲學家產生了深遠的影響，包括康德、黑格爾、馬克思和羅素。

——本文摘自《大話題：邏輯》，2023 年 3 月，大家出版出版，未經同意請勿轉載。

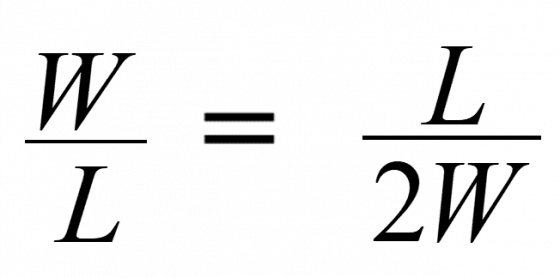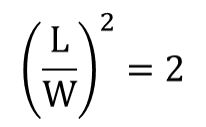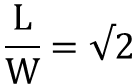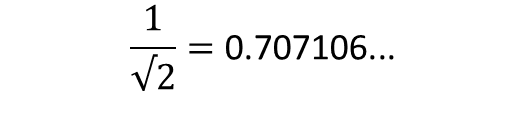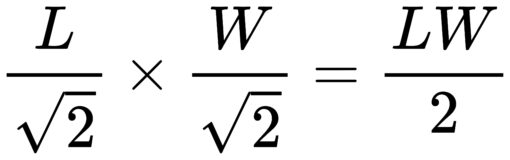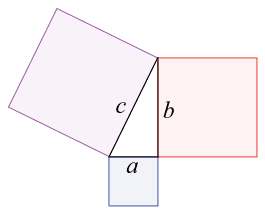
學校教過的數學課程中最讓人印象深刻的，可能是畢氏定理。

這個定理是：取一直角三角形，以直角的兩邊（股）為邊長各畫一正方形，則這兩個正方形的面積總和，會等於第三邊（斜邊）畫出的正方形面積。邊長為 a 的正方形，√2面積是 a×a = a²。如果這個直角三角形的邊長為 a、b、c，且 c 是最長邊，那麼畢氏定理得出的結果是：

a²+ b² = c²

從這個漂亮的結果，你可以算出各種東西，包括正方形的對角線長等。正方形的對角線加上兩邊，就構成了直角三角形，如果正方形的邊長為 1，由畢氏定理可知：

1² + 1² = 2 = d²

這表示對角線的長度 d 等於√2，也就是自乘結果等於 2 的數。

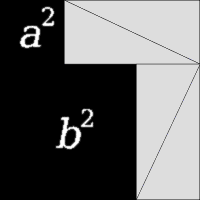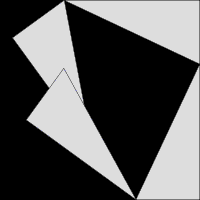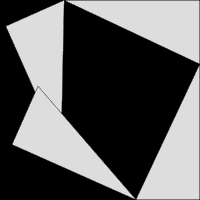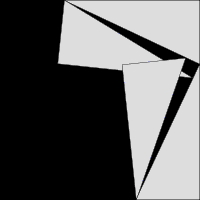
讓人有點尷尬的√2

除非你已經發覺√2有點難定出精確的數值，否則這個數沒什麼大不了的。如果拿 1.5 自乘，會得到 2.25，比 2大很多；改用 1.4，則得到 1.96，又變得太小。（1.41）² = 1.9881，還是太小，但（1.42）² = 2.0164 又會超過 2。

看起來無計可施，事實上也的確辦不到。√2是無理數，意思是無法寫出它所有的位數：完整的小數展開式是無窮盡的，而且沒有不斷重複出現的數字模式。

√2前面 20 位是：

1.4142135623730950488

發現無理數，可能招來殺身之禍

簡單的正方形對角線，無意間產生了一個性質極為有趣的數。但事實上，畢達哥拉斯（Pythagoras）的門徒不太高興。畢達哥拉斯學派是西元前五世紀活躍於克羅頓（Croton，現今的義大利）的祕密幫派，除了奉行素食主義以及不吃豆類之外，他們把求知尊為道德健全生活的基石。數學是畢氏哲學的核心：據說 mathematics（數學，意為「所學習的」）及 philosophy（哲學，意為「愛好智慧」）這兩個詞是畢達哥拉斯所創，據傳，「萬物皆數」是他的座右銘。

問題是，畢氏學派所指的「數」只有整數及整數之比，也就是 ½、¼、¾ 等分數。無理數沒辦法寫成分數；事實上，這正是定義無理數的方式（如果你熟悉長除法，就可以自行驗證，任何一個分數都能表示成有限小數或循環小數）。

希帕索斯（Hippasus of Metapontum）發現有些數（譬如√2）可能是無理數，他也是畢氏學派的一員，根據（相當隱晦的）歷史證據顯示，他因此受到嚴厲的懲罰：在海上沉船淹死。應該沒幾個人因為區區一個數而丟了性命吧？

無理但不悖理

證明√2是無理數的標準證法，是數學上經常使用的論證形式的重要範例，也就是歸謬法。要證明某件事（比方說√2是無理數），你必須先做相反的假設（√2可以寫成分數），如果之後推算出矛盾的結果，就能斷定你原先的假設一定是錯的，也就證明你最初的陳述（√2是無理數）必定為真。

這是很自然的推理方法，舉例來說，你假設管家殺了人，但如此一來，管家必須同一時間出現在兩個地方，這顯然說不通，那麼你就能推論原先的假設必定是錯的，而管家是清白的。歸謬法是數學的支柱，但也可能產生令人驚訝的結果。你將在第 3 章看到更多的例子。

希帕索斯的發現只是巨大冰山的一角。隨便取一小段數線，不管多小段，都有無窮多個無理數。那些能寫成分數的有理數，可以依序排列並賦予 1、2、3 等標籤，但無理數實在太多了，根本沒辦法用同樣的方式來區隔。你在數線上隨意一戳，碰到無理數的機率是 1，而碰到有理數的機率是 0。因此就數字而言，畢氏學派完全錯了。

√2可以是好事

假如畢氏學派知道無理數多麼有用，大概就不會因為有人發現無理數而這麼不高興了。幾乎每天都會用到的例子是紙張。歐洲採用的標準紙張尺寸 A5、A4、A3 等，有個非常棒的特點，就是將兩張同尺寸的紙並排起來，即能拼成大一級的尺寸，譬如兩張A4紙能拼成一張 A3。且小一級紙張寬度（W）的兩倍，等於大一級紙張的長度，而小一級紙張的長度（L）等於大一級紙張的寬度。

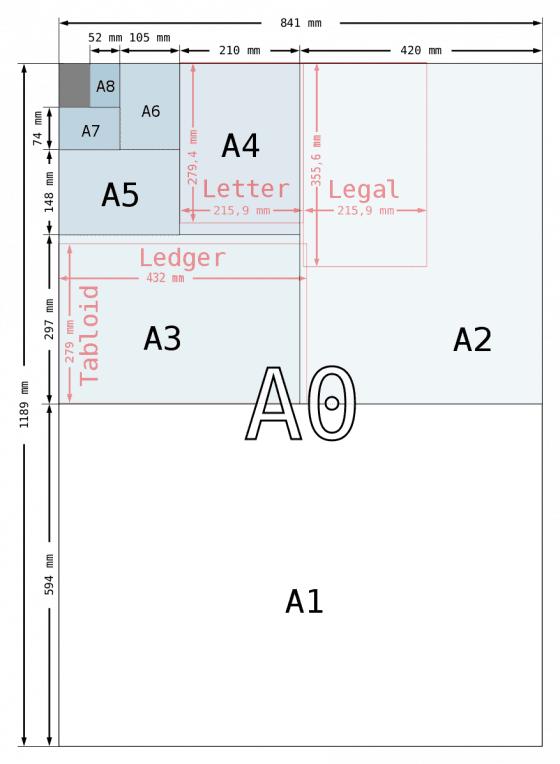
所有尺寸的紙張，長寬比都是一樣的，也就是：

可以改寫成：

意思就是：

A 系列紙張的正字標記就是每張紙的長寬比均為 √2。

為什麼這很有用？如果你希望影印機能夠把原稿縮小（或放大）一級影印，就需要此系列紙張的各個尺寸有同樣的長寬比。假如長寬比不同，縮小影印後周圍就會多出白邊。兩張同尺寸的A系列紙張可並排成大一級的紙張，代表不管你想把兩張A4還是一張A3縮小一級，都可以採用同樣的縮小倍率。

影印機還會自動計算。如果你要縮小，影印機提供的倍率是 70%，有時候是 71%，把這些數字寫成小數（70 或 71 除以 100），結果是 0.7 及 0.71，兩個數都非常接近：

這個縮小倍率，正是把一張 A3（或兩張 A4）縮小到一張 A4所需要的比例。原紙張的長度 L 與寬度 W 會縮小到 L/√2 及 W/√2，這表示新紙張的面積會變成：

就是原來的一半，且因長寬比維持不變，所以能把原來的紙張剛好縮小到 A4 的尺寸。

放大影印也是同樣的道理。影印機提供的放大倍率是 140% 或 141%，對應的數字很接近，所以可以把一張A4 放大到 A3 的尺寸。

BOX：證明√2是無理數

假設 √2 = m/n，其中的整數 m 與 n 沒有公因數（除了 1，沒有其他數可同時整除 m 和 n）。

於是：2 = m²/n²，因此：2n² = m²。

這表示 m²是偶數，m 也是偶數，因為奇數的平方永遠是奇數。所以， m 可以寫成 2k，而 k 是某個正整數。把上式中的 m 換成 2k，就得到：2n² = m² = 4k²

除以 2，就是：n² = 2k²

所以 n² 也是偶數，n 也是偶數，但這產生了矛盾，因為我們一開始假設 m 與 n 沒有公因數。因此，√2不能寫成 m/n，即為無理數。

本文摘自《數學好有事》，麥田出版。

本文由 微星科技 委託，泛科學企劃執行。

• 作者 / 曾繁安

人類總會不由自主地被閃閃發光的事物吸引，取名時加上「黃金」二字，好像就能讓身價大漲，變得受歡迎。不管是黃金海岸、黃金地段、黃金右腳、 黃金奇異果，黃金獵犬、黃金脆薯、黃金盔甲、黃金流沙包、黃金開口笑（大誤）……人們用黃金形容所有美好的事物，連「比例」也一樣。「黃金比例」被譽為最美好的比例，你一定聽聞過，如果人的臉蛋身體或畫作構圖越接近黃金比例，就越迷人的説法。然而一個數字比例，怎麼會和美學扯上關係？

人類探究黃金比例的歷史，可追溯至兩千多年前……

古希臘時代大約公元五百多年前，癡迷於數學的畢達哥拉斯，認爲數學可以解釋世上一切事物。他的教學吸引了一群熱心的追隨者，被稱爲畢氏學派。在旁人眼裏，畢氏學派恐怕是一群怪人：恪守極爲嚴格的生活條規，不可吃肉和豆類，還會進行高强度記憶力訓練和三省吾身等等。但畢氏學派對數學幾近狂熱崇拜，尤其對數字 5 和五角星形的迷戀，使他們成爲史上最早接觸黃金比例分割的一群人。將構成五角星形的線段分割，由短至長排列，把最短的兩條線段相加，恰恰等於第三條線段長；把第二短和第三短的線段相加，也會等於第四條線段，依序如是，顯示出黃金比例的奇妙！不過，他們並沒有進一步為這個神奇的發現加以解釋、定義和命名。

一直到公元前三百年，歐基里德所著的《幾何原本》問世，才有了對黃金比例最早的系統性論述。但你知道嗎？歐基里德也根本沒說過「黃金比例」一詞。後世所謂的「黃金比例」，其實是出現在《幾何原本》第四章的「極限與均值比例」（Extreme and mean ratio）。歐基里德對這個比例的說明如下：

“A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser.”

（一條線段如果切在「極限與均值比例」上，則線段的全長與較長分割段的長度比例，和較長分割段與較短分割段的長度比例相等。）

大家常常挂在嘴邊的黃金長寬比 1.618 ，就是從上圖的比例計算而來。只要把較短的線段 b 定義成 1 個單位，較長的線段 a 定義成 x 單位，再用一點國中數學上過的一元二次方程式，就能算出解答為 1.6180339887…… 或 0.6180339887…… 這兩個看～～～不到盡頭的無理數，都可被視爲黃金比例之值。就像另一位大名鼎鼎的無理數——圓周率，是以 「π」來表示，黃金比例也有自己的符號，叫做「φ」。「φ」一般念作 “ fai ” ，跟「π」押同韻，但捍衛正統希臘文念法的人可能會堅持念作 “ fee ”。

當初歐基里德只説了這麽多，純粹是為了解釋數學幾何上的意義。但他想也想不到的是，這個「極限與均值比例」，會變成美的代言人，帶給未來人類無限遐想的空間。

數學與人文藝術匯集，文藝復興時期的「神聖比例」

現代人熟知的「黃金比例」一詞，一直到 1830 年代左右才被廣爲流傳。在此之前，它的地位曾被提升到更崇高、神聖的位置。文藝復興時期，被稱為「會計學之父」的數學家兼方濟會修士——盧卡．帕西奧利（Luca Pacioli），出版了名叫《神聖比例》（Divina scalee）的著作。他從歐基里德定義的「極限與均值比例」出發，對正多面體和半正多面體的性質做討論。

帕西奧利在研究「極限與均值比例」時深受啟發，開始與他熟悉的神學進行連結。他發現這個比例中提到的三個線段（全長、長邊、短邊），都在描述同一條線，像極了基督教的神學觀，既聖父、聖子和聖靈是三位一體。而這個比值之解的無理數，所具備無法窮盡的性質，就如同凡人無法理解全能無限的上帝般，兩個線段之比例是相等的（全：長 = 長：短），則代表神永恆的不變性與無所不在的屬性。

從數學上看見神學解釋的帕西奧利，遂將「極限與均值比例」改稱為「神聖比例」。他在著作中進一步以「神聖比例」分析古希臘羅馬建築與人體結構的比例。在他看來，被神所創造的人類，其軀幹比例也隱含了「神聖比例」。這些內容更深地加強了「神聖比例」與「美」之間的連接。

此後，「神聖比例」便與「宗教」和「美」脫離不了關係。帕西奧利對純數學理論進行宗教哲學解讀的突破，成功地讓這個神奇的比例跨出數學界的舒適圈，成為數學家、神學家與藝術家之間共同的話題，後來更在討論中逐漸演變成後世蔚為流行的「黃金比例」。帕西奧利可説是打開「黃金比例」知名度，背後不可或缺的功臣。

宇宙誕生以來就存在？藏在大自然中的密碼竟是「黃金數列」

儘管吉薩金字塔和帕特農神殿是否依照黃金比例建造，數學界和藝術界還在爭辯不休，但實際上不需要人爲設計，大自然本身就蘊藏著黃金比例的美麗。以描述「兔子生兔子」問題而聞名的費波那契數列（Fibonacci number），可説是黃金比例的孿生手足。費波那契數列第零項是 0，第一項是 1，從第二項以後的值，就是前兩項加起來的和，所以依序會是：

1、1、2、3、5、8、13、21、34、55、89、144、233……

文藝復興後期鼎鼎大名的天文學家克卜勒（Johannes Kepler）發現，把費波那契數列的後一項除以前一項的值的話，會是 1 / 1 = 1， 2 / 1 = 2，3 / 2 = 1.5，5 / 3 = 1.67， 8 / 5 = 1.6， 13 / 8 = 1.625， 21 / 13 = 1.615…… 計算到這裏，你是不是也察覺到其中奧妙？隨著數列遞進繼續相除，這個值竟會越來越趨近於黃金比例！也因此，費波那契數列的別名就叫做「黃金數列」。

大自然中的植物，其實都是深諳造物奧義的數學大師。試著數一數雛菊的花瓣數量，你會發現它們恰好都是 13、21 或 34 的費波那契數。葉子與葉子之間要怎麽喬位子，才不會擋住彼此吸收陽光？玫瑰的花瓣要如何排列，才會顯得漂亮對稱？松果上的種子要怎麽生長，才可以有效利用有限的空間？這些問題的答案通通都是：旋轉角度的比值（以 360° 為分母）要符合黃金比例！

不只是植物界，無論是鸚鵡螺貝殼的生長、鷹隼迫近獵物的飛行軌線，抑或衛星圖上熱帶氣旋的外觀，就連宇宙中漩渦星系的旋臂，都呈現遵循黃金比例的螺線。從小至可一手掌握的貝殼，大至遙遠光年之外的星系，都藏著黃金比例的身影。大自然對這個奇妙比值的鍾愛，讓科學家着迷不已。

有生命的動植物和無生命的氣旋或星系，都不約而同服膺於一個神奇的比值，展現一種似乎自世界誕生以來就存在，難以撼動、一致而規律的美。同屬於大自然一份子的人類，也不停在各樣的建築或藝術品中追尋，渴望證明黃金比例與美的相關性。然而即使是世人眼中曠世巨作的大衛像，也沒辦法百分百貼近黃金比例，畢竟誤差永遠不能被全面消除，更別忘了有限的我們也無法窮盡無限的 φ 。正因爲黃金比例是一種人類無法徹底掌握的美，才迫使我們得以在追求美的道路上，不停努力地前進，再前進。

連自然都青睞的「黃金比例」近乎是「美」的同義詞。而我們的身邊，又有什麼東西用到黃金比例呢？

沒錯！就是這台 Creator Z16 筆記型電腦。

採用 16 : 10 螢幕的 Creator Z16 ，比市售的 16 : 9 螢幕多了 11% 的可視空間，創作更加自由寬廣。此外，16 : 10 ( 1.6 )也非常接近黃金比例（ 1.618 ），讓你在創作時，感受蘊含萬物奧秘、數學家兩千多年來淬鍊的「美」。

本著以人爲本的設計理念， Creator Z16 的觸控面板讓人可更直覺操作，隨時揮灑靈感。 90 Whr 的大容量電池搭配快充功能和 15.9 mm 纖薄金屬打造的 2.2 kg 機身，可完美配合現代人隨時行動隨地工作的步調。以 True Pixel 顯示技術打造的 QHD+ 超高畫質面板，加上獨家 True Color 技術於出廠前進行色彩校正，可以精準呈現璀璨畫面。

想堅持你對生活的美學，又不想放棄實用主義的追求？小孩子才做選擇，你可以通通都要！就讓融合黃金比例又兼具堅强實力的 Creator Z16，成為你的繆思女神吧！

現在購買 Creator Z16 加贈價值 2190 元 Microsoft 365 個人版一年期！登記再抽潮到出水的 Porter 托特包，這麼好康還不快點到賣場逛逛！

參考文獻

• 作者／大衛．翁弗拉許；譯者／林柏宏

科學的起源：以真實性質的角度來理解自然

二十世紀物理學家理查． 費曼（Richard Feynman，1918-1988）認為，當代物理學奠基於巴比倫人的數學方法，他們會以數學的方式來闡述問題，這種經驗能夠讓人學會歸納，進而發現自然原理。歐幾里得（Euclid ofAlexandria，西元前三世紀中期到西元前 285 年）的治學方法則與此相對，這位希臘思想家運用基本的邏輯規則，從我們稱為公設的基礎事實推導出更多複雜的定理。

在大約西元前三百年時，歐幾里得的方法很流行，而他的演繹法發源於更早的幾世紀前，當時的希臘思想家剛開始大膽地以真實性質的角度來理解自然。

對於月亮、太陽與眾行星性質的了解要真正有所進展，希臘的天文學家就得接受量化的方法。他們會需要巴比倫人研究天文的方法，包含實際數學運算，以及從單調的天象觀測中蒐集大量資料。他們的研究必須將這些資料融合希臘文化特有的、探討本質的思維。這種思維是從西元前六世紀的愛奧尼亞人社群開始的。

愛奧尼亞地區位於今日土耳其西部沿岸的城市與島嶼，最早開始推斷大自然是可探究、可預測的希臘人都來自這一帶，他們認為大自然的運作與眾神的意志無關。這種去除神祕面紗的世界觀由米利都的泰利斯起頭，從而解放了愛奧尼亞人的思考，開始為自然現象提出物理學的解釋模型，對科學的進步發揮了重要作用。

然而，希臘世界另一邊的哲學家都反對泰利斯的論點，這些哲學家的根據地是位於南義大利的希臘殖民地─大希臘（Magna Grecia）。

在這場論爭裡，一些大希臘區的哲學家其實是最早發現月亮是球形而非一圓盤的人，有一批大希臘的人還引進了會讓希臘天文學突飛猛進的數學知識。但是，大希臘區並無科學思維，這裡的人高張神祕主義，鄙視實證精神，影響力最大的神祕主義團體還掩蓋、打壓與其主張相左的新發現。

諷刺的是，這個神祕主義勢力團體的創始人，出生於愛奧尼亞區中心地帶薩摩斯島（Samos）的畢達哥拉斯（Pythagoras，約西元前 570-495），其實就學於泰利斯門下，並由此展開他的學術之路。

泰利斯預測日食，阻止戰爭

要是西元前二千六百年就有諾貝爾和平獎，肯定會頒發給米利都的泰利斯。

他出生時，正是巴比倫文明崛起，催生出前所未有的知識創發活躍期，他也漸漸愛上數學與天文學。愛奧尼亞隸屬於呂底亞王國（Lydian），不過泰利斯或許去過巴比倫，不然就是取得了巴比倫的天文學文獻。不管是哪種情形，泰利斯都認識到日食與月食的沙羅週期，這與他的想法不謀而合，他本來就認為神明與自然無涉。

當時呂底亞正與其敵對國之一，米迪亞（Media）交戰，泰利斯知道雙方指揮官都是迷信的人，便提出警告說，眾神要求他們休兵，並且會在西元前五百八十五年春季的某一天使太陽暗下來，以表明神意，其實泰利斯根據沙羅週期進行計算後，已經得知這一天應該會發生日食。

儘管泰利斯自己未察覺，但當他如此運用沙羅週期時，實際上計算的正是月球在太陽前方的移動。總之，日食確實出現了，戰事也平息了，泰利斯在愛奧尼亞聲名大噪，想向他學習自然研究的人蜂擁而至，其中一位就是從薩摩斯島搭船前來的畢達哥拉斯。

當時的米利都是個富庶的港口城市，當地的希臘居民不願向帝國統治者效忠，他們獨立自主，擁抱新知，或許是因為常從各地的航海貿易商口中得知新觀念，長此以往，泰利斯與其他米利都人的思考方式開始變得新穎激進。

比方說，他們認為地震是由於海中巨浪擊打陸地，土地陸塊是來自海水淤積堆造而成。這些關於自然的解釋終究會被證明並不正確，但重要的是，當時他們的想法和其他地方的人不一樣，他們的想法是可以接受驗證、有可能被否證推翻的，與那些虛無縹緲的神明無關。

泰利斯和在他之後的愛奧尼亞人之所以與眾不同，乃在於他們斷定，認識自然是可行的，可以接受觀察與分析─ 而且，對於他們之中某些人而言，也能透過試驗實證。

為封口無理數的發現而殺人的畢達哥拉斯

薩摩斯的畢達哥拉斯是目前已知世上最早指出月亮是球狀的第一人，他會這麼想或許一開始源自觀察的結果，例如發現月球明暗分界線（lunarterminator）是彎曲的，這道線區分了月球被照亮與未被照亮的兩部分。

畢達哥拉斯畢竟是泰利斯的學生，而且比同時代的人更早認出晨星（the MorningStar）與暮星（the Evening Star）是同一顆物體─ 金星。這種認知來自於觀察，雖然畢達哥拉斯後來排斥觀測，轉而堅持藉由純粹的思索即可了解宇宙。

旅居埃及多年，又去了巴比倫之後，畢達哥拉斯帶來了一項定理，直角三角形斜邊圍成的正方形面積，等於兩短邊各自圍成正方形的面積和。這不是他自己想出來的，埃及人與巴比倫人早將這觀念實際運用在生活中好幾百年了，巴比倫甚至發展出三角學這門數學。無論如何，由於畢達哥拉斯將這個定理引介給希臘人，未來幾世代探究大自然所需的數學知識才有機會出現。

但對畢達哥拉斯而言，數學不僅是工具，而是宗教信仰。

球狀月亮的想法只是畢達哥拉斯兄弟會神祕思想的一部分，畢達哥拉斯在位於義大利的克羅敦殖民地（the Croton colony）創立了這支教派。畢達哥拉斯教徒主張天界的「星球和諧」，認為月亮與其他星體不只是球形，而且是完美球形，繞著絕對的圓旋轉，每顆星球會產生特定的音符。再加上畢達哥拉斯輕視觀測法，凡是和其完美和諧觀念牴觸的新發現都一貫打壓。

其中一例是他的學生發現數字 2 開平方根會得到無理數，也就是無法化作分數，不能以兩個整數做為分子與分母來表示。謠傳畢達哥拉斯為了封口，謀殺了那個學生。

但他並不需要依靠暴力來提倡自己的學說。不久後，柏拉圖（Plato，約西元前 427-347）將熱心採納畢達哥拉斯的神祕主義，包含那些完美球形、圓形軌道、對觀察實測的輕蔑，以及阻撓接下來幾世紀科學進展的一切花俏玩意兒。

採納實證主義的亞里斯多德

和他的老師柏拉圖比起來，亞里斯多德比較有科學精神。

雖然兩人的出發點都是想將畢達哥拉斯、巴門尼德提倡的這類神祕主義哲學與愛奧尼亞人的自然主義整合在一起，柏拉圖終究傾向了神祕主義，亞里斯多德則對愛奧尼亞思維更有好感。若提到愛奧尼亞的實證主義（empiricism）── 主張知識必須透過感官作用的經驗才能取得，兩人的分歧會特別明顯。

愛奧尼亞人泰利斯觀察尼羅河的沉積土層後，做出了假設，認為全世界的大塊陸地都是經由類似過程，從一原始大洋中形成的。而泰利斯的學生、米利都的阿那克西曼德（Anaximander of Miletus，西元前 610-545）觀察幼魚和人類的差異，並在看過化石骨骼後，構想出早期版本的生物演化假說。綜合他們的所見所聞，愛奧尼亞人了解到，大自然不停地在變動。

亞里斯多德在研究如生物這一類地球上的物質時，大致上採納愛奧尼亞式的實證主義與變化觀念，可是一旦主題來到天象，他就表現出神祕主義的遺緒。畢達哥拉斯有個很妙的想法，認為天上的星體都是繞著正圓形軌道轉的完美球形，亞里斯多德深受此思想荼毒，同時還採用巴門尼德的主張，認為萬物恆定不變，結果形成了以下觀點：

星星、太陽與行星都是恆久不變的，有永遠固定的幾何形狀，地球是墮落不潔的，也因此不完美。違背這完美理念的還有月球表面的暗黑地貌，亞里斯多德對此的解釋是，月球和地球走太近了，太靠近存在於地表上的汙染，指的就是人類和其他生命形式。

——本文摘自《月球之書》，2019 年 9 月，時報出版。