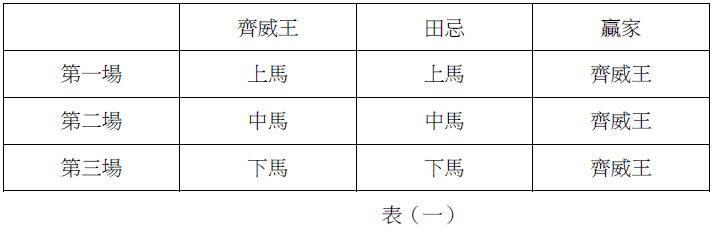
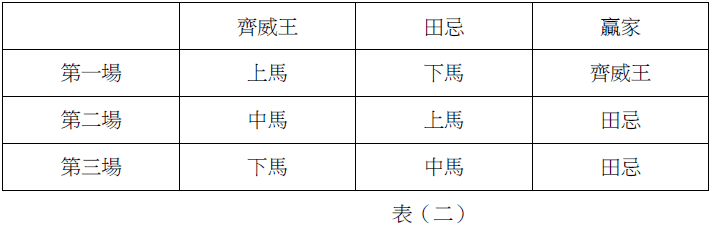
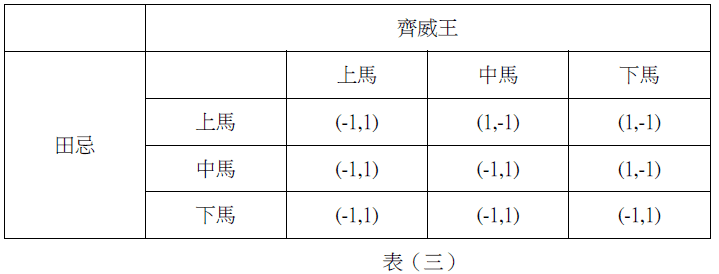
「數感盃青少年寫作競賽」提供國中、高中職學生在培養數學素養後,一個絕佳的發揮舞台。本競賽鼓勵學生跨領域學習,運用數學知識,培養及展現邏輯思考與文字撰寫的能力,盼提升臺灣青少年科普寫作的風氣以及對數學的興趣。
本文為 2018數感盃青少年寫作競賽 / 高中組專題報導類佳作 之作品,為盡量完整呈現學生之作品樣貌,本文除首圖及標點符號、錯字之外並未進行其他大幅度編修。

- 作者:陳冠伊、柯喻朦、陳品彤/北一女中
2010 年上映的電影《關鍵救援 72 小時》,由羅素克洛(Russell Crowe)飾演的男主角 John,為了拯救被無辜關入大牢中的愛妻,從一位文質彬彬、溫和善良的大學教授,想出了劫獄的計畫,只因為他始終相信自己心愛的妻子是被冤枉的!原本有點懦弱的 John,開始著手準備計畫逃亡路線,籌措資金,觀察監獄地形。一開始他將自己上網看影片學做來打開監獄大鎖的陽春鑰匙,因為緊張到發抖而折彎,他跟黑幫混混們打交道,卻被打得渾身是傷,但後來他漸漸的轉變,他誤殺了幾個人,搶了錢,但他知道這些都是為了自由與愛。看著 John 的轉變,以及善良與使命的矛盾內心戲,更是將電影一次又一次的推到高潮!其中重要的一個片段,就是 John 第一次開始著手準備劫獄計畫,向由連恩尼遜飾演的有名逃獄專家請教逃獄時該注意的事項了!
這個片段迷人的不只是連恩尼遜帥氣的低沉嗓音,更是讓我們對封鎖域大開眼界。電影中敘述只要 15 分鐘警方即可封鎖匹茲堡市中心,35 分鐘內所有洲際收費站都會有警察站崗,二級公路還會開始進行管制!John 在地圖上以市中心為圓心畫了一圓,此即為警方可封鎖的範圍,在這個封鎖域的範圍下,誰都難逃警方的法網,只能乖乖束手就擒!
於是這引起我們的好奇,匹茲堡這麼大,警察們到底手腳要多快,才能避免飆車中的 John 在圍好封鎖域前就逃出呢?
首先我們得知道匹茲堡到底有多大,經過查詢資料,匹茲堡所在的都會區約為 10000 平方公里,以此為圓面積所做出來的圓,半徑為 56.42 公里。(在此取56以方便計算)而封鎖域的總長度,也就是圓周長,則是 351.85 公里。假設以 John 出發的點為圓心,做一個半徑為 56 公里的圓,這就是警方的封鎖域。John從圓心到達封鎖域的邊界,最短距離為 56 公里。他必須在警方封鎖之前的 35 分鐘內逃出去遠走高飛,才不會被警察一槍斃命!因此 John 在不碰到任何建築物及阻礙物還有剛好天助般的都是綠燈,並且有條剛好就是半徑的馬路可以讓他在市區內盡情飆車的情況下,他的最大速率為 56 × (35/60)=96 公里/小時。
接著我們搜尋了匹茲堡的警力狀況,查詢匹茲堡警察局網站顯示目前約有 900 位警力,以 9 人為一小組,共有 100 組,而他們要在 35 分鐘內就將自己的轄區圍得天衣無縫!如此一來,一分鐘內總共得圍好 351.85÷35=10.05 公里,每一組則須完成 10公里÷100組=0.1 公里,也就是100公尺,一個人一分鐘則須圍好 11.1 公尺。若是像臺灣的凱達格蘭大道一樣,每次有重大事件總是用拒馬圍得密不透風,一分鐘把這麼重的拒馬和鐵欄擺好 11.1 公尺,實在是有點困難啊!
以 John 有最大速度 96 公里/小時,並且不外調人員,總共只有 900 位警力負責封鎖的狀況下,要能及時圍住整個封鎖域的範圍是極具挑戰性的。因此,我們開始思考是否有什麼策略,能提供警方一個在最短時間內,一定能圍住 John 的方法呢?
查詢了許多資料以後,我們找到了一篇提供我們策略構想的數學論文:The Angel Problem (引注資料[1]),由 John H.Conway(沒錯也是 John,但此 John 非彼男主角的 John)於 1996 年發表。這篇論文主要在研究天使問題,這是一個雙人遊戲,而遊戲規則是:
在一個無限大的棋盤上,有一個惡魔跟一個天使,棋盤一開始是空的。開始遊戲後,天使在每一輪都可以移動最多 K 步(遊戲開始前先設定好的,稱之為天使的力量),在這 K 步中,橫的直的斜的都算一步,而且天使可以飛越過惡魔設置的路障,但是最後必須停留在沒有路障的格子內,而惡魔每一輪只可以選一個格子設置路障,但不能設在天使停留的那個格子。最後,如果天使無法再移動時,就代表惡魔贏了,相反的,如果天使可以無限的移動的話,則代表天使贏了。
康威在他的論文中,所假設的情境是:每次只能移動一格的惡魔,是否有機會可以困住天使的力量為 1000 的天使呢?這看起來是不可行的,但是康威提出了在一些假設的條件下,惡魔能夠以區區的一步,困住能飛 1000 步的天使!有趣的是,康威甚至在論文的最後,提出懸賞 1000 美金,給能夠找到證明惡魔可以困住力量為任意數(但不能為無限大)的天使的人!
我們運用了康威假設的其中一個情境的方法來發想,是否一樣能應用在警察和逃亡中的 John 這個情境中呢?
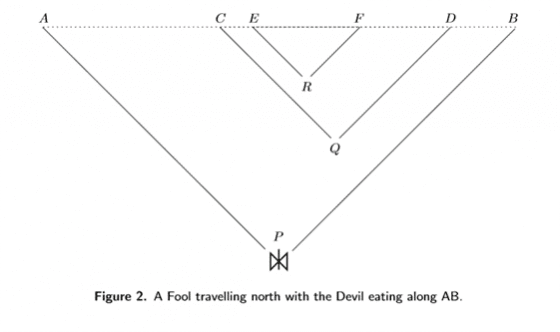
康威假設有個 Fool Angel,他只能不斷的往上飛,增加他的 y 座標,此時惡魔將會有必勝的方法圍住天使。天使的起始點為 P,由於不浪費步數,因此他的飛行範圍介於通過 P 點,兩條斜率為 ±1/1000 的邊界內。則惡魔的必勝策略為:圍住一條與起始點足夠大距離(H=1000×2N) 的邊 AB ,並在開始時每 M格放一路障,在天使達到距 AB邊 1/2H 距離的點Q 時,惡魔已經完成在 AB 以 M 為間隔的路障擺設。當天使在點 Q 時, CD邊正好是 AB邊的一半,而同樣的惡魔也在 CD 邊上,每 M 格放一路障,當天使抵達了距離 AB 邊 1/4H 距離的點R 時,惡魔已完成 CD 線段。如此一來,當天使飛到了距離 AB 邊 H’=2-MH 距離的點時,惡魔已經在AB 線段上的每一格放滿了路障。若 H為 1000×2N,1000 為天使和惡魔的速度比值,且 N>1000M,則在天使跨越距離 AB線段 1000單位距離時,惡魔早已在這條水平線和 AB 線段間的任何天使有可能到達的格子內,放滿了路障!
有了康威的天使遊戲做為參考,在我們所設定的情境裡,H 為警方封鎖域的半徑 56 公里。我們可以將天使的力量想像為 John 的最大速率 96公里/小時,惡魔可以走的步數則是警察每分鐘的封路速度 0.1公里/小時。代入康威所提供的算式 H=1000×2N 中,我們姑且將 56 公里取為 2 的整數次方倍 64 公里較方便計算,John 和警察的速率比為 960 公里/小時,相當於 16 公里/分鐘,因此計算結果為:
64=16×2N
N=2且N>16M,經過計算可知,M為 1/8 公里,相當於 125 公尺。
也就是說,若匹茲堡的警察們,比照康威所提供的方法,每 125 公尺就設置一個路障,待 John 到下一點時,再從對應到的水平線距離兩端繼續往內圍,如此一來,John 勢必將被團團圍住在封鎖域中,無法逃之夭夭!
雖然電影的最後,John 當然是突破重圍歷經難關,帶著妻兒離開了美國展開新生活,但是若有下一位逃犯,我們想匹茲堡的警察一定能將我們所提供的封鎖域策略派上用場的。
當 John 向連恩尼遜請教逃獄方法時,連恩尼遜最後問 John,在著手準備逃獄前,比所有方法都還更重要的是,你真的覺得自己做得到嗎?
看似不可能圍住天使的惡魔,原來也能圍住比自己擁有還要強大許多力量的天使;看似不可能在短短時間內就將 10000 平方公里大的都會區圍得密不透風,經過我們的推理計算,原來也有絕佳的保證策略能夠達成目標;看似不可能做出瘋狂逃獄計畫的溫和大學教授,為了愛為了自由,甚至為了正義,在 John 的轉變中,我們看著他一步步,將不可能轉化為可能。
只要我們相信,我們做得到。
引注資料[1]: John H. Conway (1996). The Angel Problem.