投資策略研究
「 2000 年受臺大財金系合聘之邀,我開了一門『財務統計』課程。當時股市正值科技泡沫,我很好奇為什麼會有這個現象,加上受到財金系同事和學生的耳濡目染,漸漸覺得財務的『實證研究』蠻有趣,就一直研究到現在……」
研究室位於中研院統計所的迴廊深處,何淮中像個隱士般。置身股市戰線之外,以嚴謹的統計模型、歷史的股市資料,驗證股票市場的理性與不理性。

投資人有理性嗎?
但 2017 年獲得諾貝爾經濟學獎的 Richard H. Thaler ,曾經做一個有趣的實驗,闡述另一位諾貝爾經濟學獎得主 Herbert Simon 所提的「有限理性」(bounded rationality),證明人沒有辦法完全理性。
Richard H. Thaler 在 1997 年 5 月於《金融時報》(Financial Times)刊登一則活動廣告,希望大家來報名參加 “pick a number game” ,大獎是英國航空往返倫敦與紐約/芝加哥的機票。玩法很簡單,只要玩家在 1~100 中選一個整數寫在信中、寄回主辦單位,截止後將所有收到的數字蒐集起來「取平均數、再乘以三分之二 」 ,最靠近這個數字的玩家,就是贏家。
假設 5 個人參加比賽,他們選擇 10,20, 30, 40 和 50 ,在此情況下,平均數是 30,而 30 的三分之二是 20 ,因此最初選擇 20 的玩家是勝利者。
這遊戲的隱含意義是──人們的預期心理、有限的理性。
若按照「市場是理性」假說,所有玩家應該會預期別人選擇什麼數字、並取平均數再乘以三分之二;然後又預期別人應該也會這麼做,又再取平均數再乘以三分之二……;經過這樣的循環,直到最後每個人都會選擇 1。
但無論是 1997 年《金融時報》這次、或我在各場合玩這個遊戲,都發現理性是有限的,人們一開始只會猜測別人的答案兩到三次循環,然後就選一個直覺大概沒錯的數字。
不同市場群體,會理性到什麼程度,我們可能不知道,就需要蒐集資料、根據統計來估計,這就是統計的重要性。
預期心理是什麼?
但其實台股的「菜籃族」常常搞不清楚股票上漲或下跌的原因,聽聞小道消息就跟風「追高殺低」,導致損失慘重。其實這背後有「動能效應」可以解釋,1993 年由 Jegadeesh and Titman 提出,指的是股票報酬率有持續性的現象,強者恆強、弱者恆弱。
動能效應是什麼?
投資人會有預期心理,預期心理又受到小道消息影響。由於小道消息的資訊傳遞像漣漪一層層擴散出去,因此股價在一定期間內呈現漲繼續漲、跌繼續跌,好像有個「動能」在持續推高或拉低股價。
動能投資策略,就是運用這種現象來規劃投資組合:買進贏家股票(漲繼續漲)、搭配賣出輸家股票(跌繼續跌)。
然而,2000 年之後的股票市場,這種動能效應似乎消失了。有些人認為是因為大家都知道這種賺錢方法,有些人認為是時機不對。但我們認為動能效應應該還存在,只是被一些「雜訊」給掩蓋,所以就撈出 1930 年 1 月到 2010 年 12 月的美國股市資料,和學生一起設計我們的「WL-LH 動能投資策略」做實證研究。
實證研究有哪些發現?
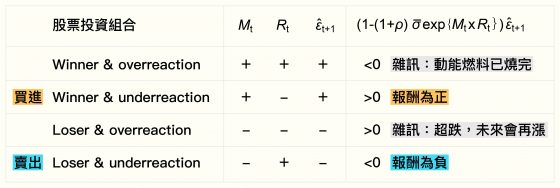
其實這與過往的動能投資策略差不多,差別在於,我們透過美股歷史資料分析,於投資策略中刪掉一些「雜訊」:「漲幅被高估」的贏家股票,也就是動能燃料已經燒完、會開始下跌;還有「跌幅被高估」的輸家股票,因為超跌、未來會再漲回來。這兩者分別代表投資人對於市場中好與壞的資訊,呈「過度反應」的現象。
困難的是,如何判定漲幅或跌幅是否被高估?我們從「資訊擴散」的角度出發,提出一個資產價格模型。然後藉由價格模型,設計一個價格風險指標,有效地篩選掉超漲或超跌的股票,從而驗證了市場的預期心理和動能效應,也同時說明市場的不效率性。
其中相關的統計模型算式,通常大家看了就頭痛,這裡先不贅述,有興趣的朋友請直接看看我們的論文。
從 1930 年 1 月的資料開始,我們先看過去一年的累計複利報酬、排序,買表現好的股票、賣表現壞的股票,一個月後檢視這樣的投資組合的報酬率。因為資料時序已經移動一個月,所以我們再從新的一個月回頭看過去一年的累積複利報酬、排序,再進行一次剛剛說的投資。
最後把累計複利報酬取平均值,例如下圖的 2000 – 2010 年資料所示。其中可看到, 2000 年以後的動能效應,原本大家認為已經消失了,但經由我們的 WL-LH 投資策略挖掘,失而復得,動能投資策略的獲利空間仍然存在。
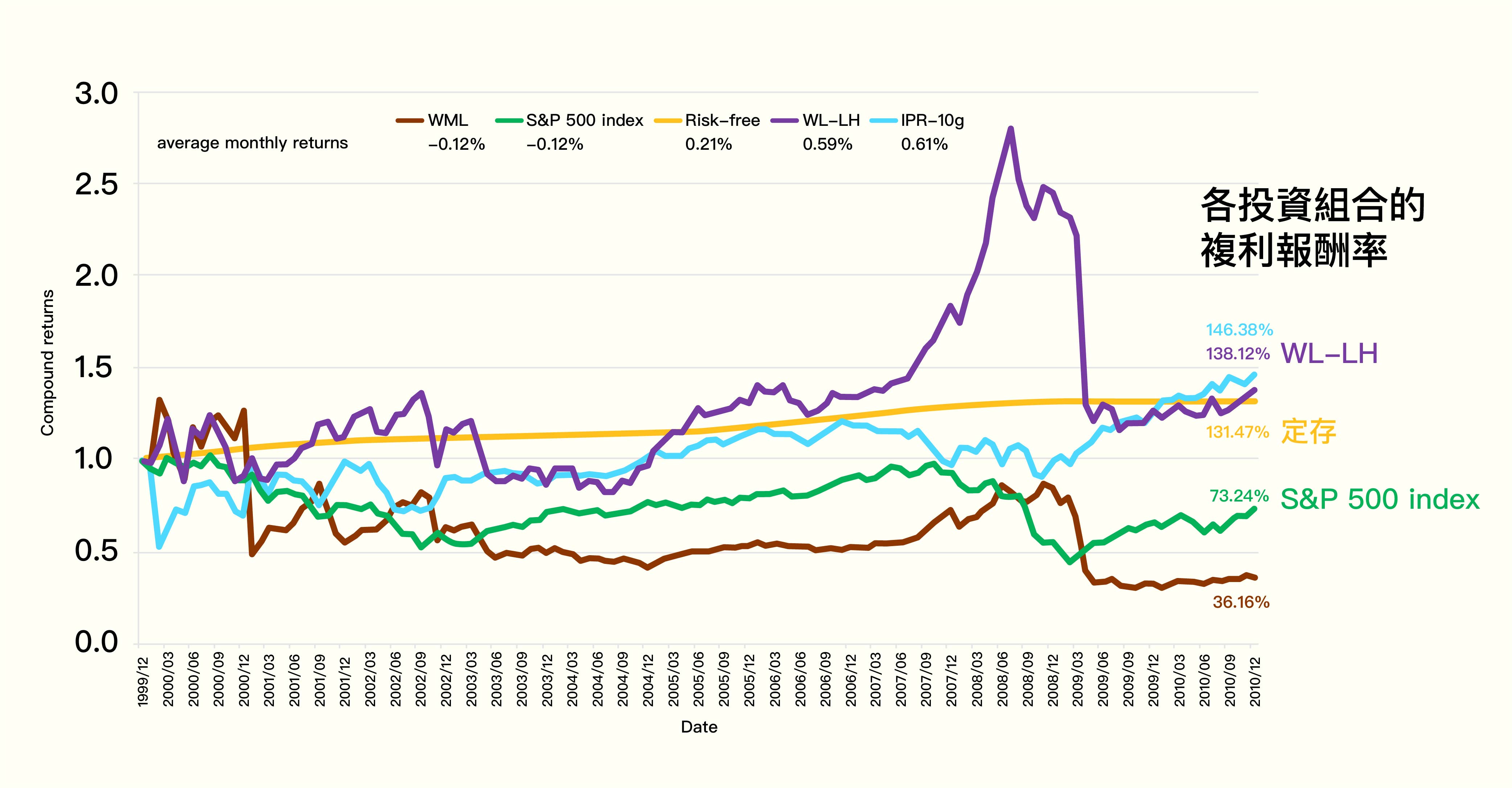
若把這個動能投資策略,套用至不同國家市場,有不同表現嗎?
我們對這個詮釋抱持懷疑,所以我們試著將 WL-LH 投資策略,套用至不同國家股市的歷史資料(1990-2014 年)驗證,發現只要去掉「雜訊」──上漲動能燃料已燒完的股票、以及超跌的股票,無論是美國、歐洲、日本、印度等 21 個國家,都能看見動能效應,比率接近九成。
換言之,因為人們投資行為的偏誤,例如貪婪追高股價、恐懼在低點持股,而導致市場的不效率性,是超越地域、族群而存在的共通現象。
但是台股比較特別,在 WL-LH 策略下,仍看不到動能效應。
在台股歷史資料(1990-2014 年)中,刪掉漲幅「被高估」的贏家股票、跌幅「被高估」的輸家股票後,並未找到動能效應。我們的推斷認為,台股投資人普遍容易過度預期,以及股票交易周轉率較高,可能是主要的原因。兩者都影響了模型預測「資訊擴散程度」的準確性。
話說回來,為什麼會喜歡統計呢?
由機率跨入統計,是很自然的。兩者都是處理「不確定性」的方法體系,密不可分。
我的研究,包括前面提到市場效率性的課題,「機率」與「統計」兼而有之。透過資料分析,可以證實股市有一定程度的不效率性,也有獲利的空間。但投資仍有風險,不會因為這些研究發現就產生過度自信,所以我老婆和我還是存定存、買共同基金。再說,她的錢我也管不了呀。
延伸閱讀
- 何淮中的個人網頁
- Hongwei Chuang and Hwai-Chung Ho (2014). Implied price risk and momentum strategy. Review of Finance 18, Issue 2, 591-622.
- Hwai-Chung Ho and Hsiao-Chung Wang (2017). Momentum lost and found in corporate bond returns. Journal of Financial Markets (MOST Finance Atier-1). Accepted.
- Chun-Yo Chen and Hwai-Chung Ho (2018). Price Risk and Momentum around the World: Buy Low and Sell High.
本著作由研之有物製作,原文為《行情總是在希望中毀滅? 專訪何淮中》以創用CC 姓名標示–非商業性–禁止改作 4.0 國際 授權條款釋出。
本文轉載自中央研究院研之有物,泛科學為宣傳推廣執行單位