豬流感捲土重來？防疫戰進退失據！｜科學史上的今天：2/4

本文與 Panasonic 合作，泛科學撰文 

●以下科學研究內容作為知識分享，不直接與Panasonic A La Uno全自動洗淨馬桶產品功能連結

在做家務的痛苦排行榜上，「刷馬桶」絕對名列前茅。明明天天都在沖水，但過不了幾天，馬桶內壁邊角總會浮現黃黃的水垢、角落發黑的霉斑，甚至是那些刷掉又長出來的粉紅色污垢（黏質沙雷氏菌）。

許多市售衛浴設備常標榜「神奇抗污」或「永久不沾」，讓人誤以為安裝後便能永保潔淨。然而從材料科學的角度來看，世上並無能使污垢憑空消失的魔法。所謂「耐污」的實質機制，並非打造完全不沾染髒污的材質，而是調整表面的物理與化學屬性，使水垢和微生物難以強力附著。一旦降低了污垢與內壁之間的附著力，透過日常水流沖刷，便能輕易地將髒污帶走。

為什麼污垢「黏不住」？ 

要搞懂為什麼某些特殊表面能做到「耐污」，我們得先像偵探一樣，拆解馬桶裡的髒污究竟是怎麼「抓緊」材料表面的。馬桶內壁的污垢主要有兩大難纏的元兇：

1. 水垢與礦物沉積*1：我們日常使用的自來水中含有鈣、鎂等金屬離子。當水滴在表面經歷反覆的濕潤與蒸發乾燥循環時，這些離子會逐漸結晶析出，變成硬度極高、緊緊「卡」在微觀縫隙裡的礦物質水垢。
2. 生物膜與有機物*2：包含尿液中的無機鹽、油脂殘留，以及細菌入侵後分泌出像超強膠水一般的聚合物，所組成的黏滑防禦大本營。

這兩大類污垢想要在材料上「落腳」，前提是它們必須能在表面找到足夠的附著點與黏合力。那麼，材料科學家是如何讓這些髒污「站不穩」的呢？答案就藏在「表面能（Surface Energy）」與「濕潤性（Wettability）」這兩個核心概念中。

當我們把水滴在某個表面上時，水滴會聚成一顆圓滾滾的水珠，還是迅速攤平開來？這取決於表面的特性：

• 疏水路線（Hydrophobic）*1：具備低表面能的疏水表面，能顯著減少水分子或污染物與表面之間的極性作用力與氫鍵。水滴在這種表面上會因為表面張力而收縮成水珠，當水珠滾動滑落時，就能順便把表面的灰塵與礦物質顆粒帶走，這就是著名的「自清潔效應」。
• 親水路線（Hydrophilic / Superhydrophilic）*2：相反地，極度親水的超親水表面則會強烈地吸引水分子，在材料最外層形成一層薄薄的「水化層（Hydration Layer）」。這層水化層就像是實體的液體盾牌，讓油污、蛋白質或細菌無法直接接觸到材料基底，只能漂浮在水膜上方。

如果要用攀岩來比喻：傳統粗糙的表面就像是有許多凹槽的攀岩牆，髒污就像攀岩者，需要找到落腳點並用力撐住才能攀附；而我們做的是抽掉把手點，或是在把手上塗上潤滑油，讓髒污找不到施力點，自然難以停留。

不給細菌「握手」的機會

解決了水垢，下一個更棘手的對手是「細菌」。

馬桶內壁那些黑黑粉粉、摸起來滑滑的污垢，在微生物學中被稱為「生物膜（Biofilm）」。細菌並不是孤立生長的，當單顆細菌落在表面後，如果覺得環境舒適，它就會開始分泌胞外聚合物（EPS），這是一種天然的超強膠水。細菌們用這種膠水把自己與同伴緊緊黏在一起，並築起堅固的防禦堡壘，這時一般的沖水就很難把它們沖洗乾淨了。

根據《Nature Communications》與《Microsystems & Nanoengineering》的學術期刊研究指出，要阻止生物膜形成，除了化學上的抗菌，材料的「表面微幾何結構」扮演了至關重要的角色。

材料科學領域中有一個著名的「附著點理論（Attachment Point Theory）」：

1. 粗糙與微孔洞表面：如果材料表面存在許多微小的裂縫、氣孔或微米級凹洞，細菌（體積通常約 1 到 3 微米）就會興高采烈地鑽進這些小凹槽裡。這些凹槽不僅提供了極佳的機械咬合支點，還能幫細菌擋掉水流的沖刷。
2. 極致平滑與微結構表面：相反地，如果材料表面做到極致平滑，完全沒有微米級的缺陷；或者反過來設計出尺寸遠小於細菌的奈米結構，細菌的足跡構造（如鞭毛或纖毛）就無法在表面找到穩固的「接觸附著點（Contact Points）」。

當細菌發現自己在這個表面上連「手都握不緊」、隨時會被水流吹走時，它就無法順利定殖並分泌膠水築巢。此外，現代衛浴結構在設計時，也越來越強調「一體成形」與「無接縫工藝」。消除接縫與死角，等於直接拔除了細菌與水垢最喜歡的避風港。

當材料、結構與流體科技組隊聯防 

了解了材料化學與微觀幾何，我們就能勾勒出一座現代耐污馬桶的完整防禦體系：【材料層（低附著力）】+【結構層（無縫平滑）】+【動態流體層（泡沫與水流剪切力）】= 高效清潔！

以市面上備受矚目的 Panasonic A La Uno 全自動洗淨馬桶為例，就是將材料科學、結構工程與流體力學發揮到極致的典型代表：

1. 材料層：有機玻璃系新素材

A La Uno 全自動洗淨馬桶採新開發的「有機玻璃系新素材」（以壓克力高分子為基礎研發的衛浴專用材料，這類高分子成形技術亦被廣泛運用於大型水族館高壓觀景窗與飛機機艙罩）。這種材料表面具備極佳的疏水性與耐水垢特性，水滴不易長時間攤平停留；材質堅固、不易破裂，耐刮、不易造成細小傷痕。通過實驗測試，這種素材配合泡沫洗淨，在沖洗後能有效沖刷掉高達 99.99% 的大腸桿菌，從源頭阻斷細菌定殖。

2. 結構層：無接縫工藝與三重防濺防護

在宏觀結構上，A La Uno 全自動洗淨馬桶採用無水箱沖水與便器、溫水洗淨便座一體成型設計，減少傳統水箱與座體之間的結構層次及接縫，並搭配可動迴轉式排水系統完成沖洗。更貼心的是其「三重防護」設計：

• 泡沫防護：在水面上製造一層充沛的泡沫緩衝層，有效抑制男性站立小便時的尿液與污水飛濺；
• 外圍防護：馬桶邊界特別設計了高約 3mm 的水檔，防止液體延著外壁滴落至地板；
• 測漏防護：便座與馬桶本體採用不外露的防護設計，避免液體從縫隙飛濺滲漏。

3. 動態流體層：雙效泡沫洗淨、漩渦水流與 nanoe™ X

當污垢降落在馬桶內壁時，A La Uno全自動洗淨馬桶 的動態流體科技便接手進行徹底打掃。其「雙效泡沫洗淨」會先釋放直徑約 5mm 的「毫米泡沫」包裹並帶走大塊髒污，再透過直徑約 60微米的「微米泡沫」深入微觀縫隙，徹底溶解殘餘的油脂與細微污垢。接著，配合高度清潔力的「漩渦型強力水流」，利用旋轉產生的流體剪切力，一口氣將附著力已被削弱的污垢剝離並沖走。此外，Panasonic A La Uno 全自動洗淨馬桶還搭襯了 nanoe™ X 健康科技，釋放氫氧離子有效抑制異味與髒污，維持空氣與內壁的良好衛生狀態。

科技讓生活變輕鬆，但物理法則依然誠實

從材料化學的低表面能設計，到微觀幾何的附著點控制，再到流體力學的水流沖刷，一座現代抗污馬桶的演進，縮影了人類如何運用基礎科學來解決日常生活痛點的智慧。

我們習慣將衛生清潔想像成一場與細菌髒污的硬碰硬死鬥。然而，A La Uno全自動洗淨馬桶 等現代衛浴技術的突破，展示了材料科學的另一種聰明思維：不靠強酸強鹼硬打，而是透過物理與化學邏輯，將「污垢固著」的機率降到最低。

當材料科學與現代衛浴技術結合，刷馬桶不再是一件令人頭痛的辛苦瑣事。透過這些前沿科技的加持，我們得以從繁重的家務勞動中解放，享受更加乾淨、舒適且有品質的日常生活。

*1 參考論文：A metallic anti-biofouling surface with a hierarchical topography containing nanostructures on curved micro-riblets

*2 參考論文：Brushing up functional materials

• 作者／照護線上編輯部
• 本文轉載自 Care Online 照護線上《羅氏診斷女性健檢週活動開跑 HPV疫苗空窗世代別大意！定期子宮頸癌篩檢，守住健康防線》，歡迎喜歡這篇文章的朋友訂閱支持 Care Online 喔
• 加入照護線上 LINE 官方帳號，健康資訊不漏接

「即使完全沒症狀，也一定要接受子宮頸癌篩檢！」隨著羅氏診斷女性健檢週活動開跑，林口長庚婦產部教授張廷彰醫師如此表示。根據衛生福利部國民健康署 111 年癌症登記報告，子宮頸癌長期位居女性癌症死因前十名，儘管政府長年推動篩檢政策，仍有約 20% 至 30% 的患者在確診時已屬中晚期（二期以上）^[1]。近年政府積極推動 HPV 疫苗，但許多 30 歲以上女性仍屬「疫苗空窗世代」，未能在黃金施打年齡接種疫苗，此類族群更應建立定期檢查習慣。

「早期發現對子宮頸癌非常重要！」張廷彰強調，若能及時接受標準治療，一期子宮頸癌的五年存活率可超過 90%，如果進展至中晚期子宮頸癌，便可能會需要接受大範圍手術，再搭配放射治療或全身性治療，對工作及生活造成影響，存活率也比較差。

遠離子宮頸癌威脅，三道防線守護健康

子宮頸癌的發生多與人類乳突病毒（Human Papillomavirus, HPV）的感染有關，主要經由性接觸傳染，或透過接觸帶有病毒的物品造成間接感染。張廷彰指出，多數人感染後沒有明顯症狀，甚至可能自行痊癒，但有部分人感染高風險HPV後，因體質因素無法清除病毒，造成高風險HPV持續感染，持續的定義為達半年以上，進而演變為子宮頸癌前病變或癌症。

由於HPV感染與初期病變通常無明顯症狀，許多女性容易忽略定期篩檢的重要性，若等到出現異常出血等明顯警訊時，多已進展為子宮頸癌，往往已錯過早期治療的最佳時機。因此，張廷彰強調女性應透過「三道健康防線」及早防治：第一，建立安全性行為觀念；第二，接種HPV疫苗；第三，定期接受子宮頸癌篩檢，包括抹片與高危HPV DNA檢測，才能有效攔截疾病於早期，守住自身健康防線。

子宮頸抹片搭配HPV DNA檢測 助精準掌握健康風險

目前子宮頸癌的篩檢方式主要有兩種：子宮頸抹片檢查與高風險HPV DNA檢測。抹片檢查是透過顯微鏡觀察子宮頸細胞型態，檢視是否有可疑性的癌細胞存在；而高危HPV DNA檢測則是利用基因技術分析是否有感染高風險型HPV，能在病變尚未發生前就偵測出潛在風險，讓防線更提前。

張廷彰醫師建議女性可搭配兩種篩檢方式使用，以提升篩檢準確度。若HPV DNA檢測結果為陰性，代表近期感染風險較低，可每五年再進行一次篩檢，不僅能減少不必要的頻繁檢查，也能更早掌握健康風險、規劃後續追蹤。

此外，目前政府亦有相關補助政策，鼓勵女性善加利用公費資源以守護健康：

• 25至29歲婦女：每三年一次免費子宮頸抹片檢查
• 30歲以上婦女：每年一次免費子宮頸抹片檢查
• 當年度年齡為35歲、45歲、65歲女性可接受一次免費HPV DNA檢測

透過這些篩檢工具與政策支持，女性可更有效掌握自身健康，及早防範子宮頸癌風險。

9 大子宮頸癌高風險族群要注意！醫：定期檢查遠離威脅

除了公費補助對象為，高風險族群應每年做一次子宮頸抹片檢查，也建議搭配高危人類乳突病毒 HPV DNA 檢測。高風險族群包括未曾接種過HPV疫苗、較早發生性行為、有多重性伴侶、HIV 感染、接受器官移植、使用免疫抑制劑、有家族病史、反覆陰道感染、抽菸或飲酒者等。即使沒有症狀，也應該定期接受子宮頸癌篩檢，才能及早處理。

張廷彰醫師表示，自 2025 年起國民健康署擴大補助子宮頸癌篩檢，符合公費篩檢條件的女性朋友務必好好把握，若未符合資格也可自費進行篩檢，守住健康防線，也呼籲民眾「挺身而出守護健康」，主動提醒身邊女性來一場健康篩檢約會！

筆記重點整理

• 早期發現對子宮頸癌非常重要，若能及時接受標準治療，一期子宮頸癌的五年存活率可超過 90%，如果進展至中晚期子宮頸癌，可能會需要接受大範圍手術，再搭配放射治療或全身性治療，對工作及生活造成影響，存活率也比較差。
• 子宮頸癌的發生大多與人類乳突病毒（HPV）感染有關，HPV 第 16、18 型屬於高危險人類乳突病毒，可能導致子宮頸癌前病變、子宮頸癌以及男女外生殖器癌；低危險人類乳突病毒則可能會引起生殖器疣（菜花）。
• 預防子宮頸癌有三道關鍵防線，包括安全性行為、接種人類乳突病毒 HPV 疫苗、定期接受子宮頸癌篩檢。過去，子宮頸癌篩檢主要仰賴子宮頸抹片檢查近年來許多國家已開始採用 HPV DNA 檢測，因為HPV DNA 檢測能更準確預測未來罹患癌症的風險。
• 自 2025 年起衛生福利部國民健康署擴大子宮頸癌篩檢，除了子宮頸抹片檢查，還納入 HPV DNA 檢測。在子宮頸抹片檢查部分，25 歲至 29 歲婦女，每 3 年 1 次子宮頸抹片檢查；30 歲以上婦女，每年 1 次子宮頸抹片檢查。當年度為 35 歲、45 歲、65 歲的女性，可接受 1 次人類乳突病毒 HPV DNA 檢測。

參考資料：

• [1] 中華民國111年癌症登記報告

• 本文轉載自 Care Online 照護線上《羅氏診斷女性健檢週活動開跑 HPV疫苗空窗世代別大意！定期子宮頸癌篩檢，守住健康防線》，歡迎喜歡這篇文章的朋友訂閱支持 Care Online 喔
• 加入照護線上 LINE 官方帳號，健康資訊不漏接

不好意思，你很可能會得這種癌症。其實，我也是。

它就是台灣十大癌症榜首，肺癌。

現在，根據 2023 年 11 月衛福部發布的最新統計數字，肺癌一年的新增病人數已經超越大腸直腸癌，成為台灣每年癌症發生人數之最，堪稱臺灣人的「國民病」。

可怕的是，肺癌在癌症之中有三個之最：死亡率最高、發現時已經是晚期的比例最高、醫藥費也最高。現在再加上發生人數最高，堪稱從癌症四冠王。

你說肺癌是抽菸的人的事？錯！台灣抽菸人口比例在全球排名 30，比日本、韓國、中國和多數歐洲國家都還低！顯然抽菸並不是肺癌的唯一主因！那難道是二手菸？還是空污惹的禍？還是台灣人的基因天生脆弱？我們到底要怎麼做才能遠離肺癌？

臺灣人的肺癌特別在哪？癌症和基因有關嗎？

根據衛福部國健署的說法，肺癌人數的增加，其實與 2022 年 7 月開始推動肺癌篩檢的政策有關。

隨著篩檢量的上升，近年內肺癌的確診人數預期還會再往上。

原來是因為篩檢量啊，那就不用擔心了。但換個角度想，這才是肺癌最可怕的地方，它可能已經存在在很多人身體裡，而我們卻沒能發現它。肺癌早期幾乎沒有症狀，高達 50％ 的患者發現時已經是第 4 期。屆時不只肺部遍布腫瘤，癌細胞可能還轉移到大腦、骨頭等器官，讓治療變得加倍困難。

對付肺癌，最關鍵點是愈早發現愈好。按照國健署統計，如果第 1 期就發現，5 年存活率可達九成以上，第 2 期發現降為六成，第 3 期存活率大約三成，一旦到第 4 期，僅僅剩下一成。

當然，最好的方法，就是做好預防，打從一開始就不讓癌細胞誕生。

那麼我們就要先了解問題到底是出在環境，還是你、我身體中的基因？ 過去關於肺癌的遺傳研究，多半以歐美國家為主，套用到我們身上總有些牛頭不對馬嘴。幸好，我這裡一份以臺灣人為主角的大規模研究報告，將為我們揭露答案。

這份研究是由中央研究院團隊主導，結合臺灣大學、臺北醫學大學、臺中榮總等單位的研究，還登上生物領域頂尖期刊《Cell》2020 年 7 月的封面故事。非常具有權威性，不能不看。

同時，這也是全球第一次完整剖析東亞地區肺癌的成因。他們的主題很明確：「為什麼不吸菸也會得肺癌？」

在西方，肺癌病人裡面只有 20% 左右的人不吸菸。但是在臺灣，卻有超過一半的肺癌病人都不抽菸，顯示有其他致癌要素潛伏在基因裡作怪。另外，臺灣肺癌病人的男女比例和西方人也大不同，臺灣女性通常更容易罹患肺癌。 為了瞭解肺癌，研究團隊取得肺癌病人的腫瘤和正常組織，解讀 DNA 序列和蛋白質表現量，最後鑑定出 5 種和西方人明顯不同的變異特徵。

其中最受關注的，是一種 APOBEC 變異，因為它有可能是臺灣女性為什麼容易罹患肺癌的關鍵。

這種變異特徵屬於內生性的，也就是人體機制自然產生的 bug。

APOBEC 不是指單一基因，它是細胞內負責編輯 mRNA 的一組酵素，包含 11 個成員。主要功用是把胞嘧啶核苷酸（C）轉變尿嘧啶核苷酸（U）。簡單來說，APOBEC 原本是細胞正常活動的一環。但因為它有改寫核酸序列的能力，在 DNA 修復過程同時活躍時，就很有可能出事。這就像是一個創意豐富的阿嬤，看到破損的古畫，就在沒和別人討論的情況下上去東湊西補，用自己的方式重新修復了這件藝術。一個與原本不同的突變細胞可能就這樣產生了。

APOBEC 變異在臺灣女性病人身上特別明顯，舉例來說，60 歲以下沒有吸菸的女性患者，就有高達四分之三有這種變異特徵。研究團隊認為，APOBEC 出錯造成的基因變異可能是導致女性肺癌的關鍵。 除了內生性變異，另外一個容易導致肺癌發生的，就是周遭環境中的致癌物。

致癌物有哪些？

研究團隊總結出 5 種肺癌危險物質：烷化劑、輻射線、亞硝胺（Nitrosamine）、多環芳香烴（PAHs），還有硝基多環芳香烴（Nitro-PAHs）。

其中，亞硝胺類化合物主要來自食品添加物和防腐劑，多環芳香烴大多來自抽菸和二手菸，硝基多環芳香烴則是透過汽機車廢氣和 PM2.5 等毒害肺部。

他們進一步分析，大略來說，女性在不同年紀，致癌因素也有差異。60 歲以下的女性肺癌病人，APOBEC 特徵的影響比較明顯；70 歲以上的女性患者，和環境致癌物的相關度比較高。 既然找到致癌原因，我們該如何著手預防呢？你知道肺癌，其實有疫苗可打！？

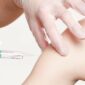
空氣污染和肺癌有關嗎？有沒有癌症疫苗？

想預防肺癌，有 2 種對策，一種是「打疫苗」，一種是「抗發炎」。

是的，你沒聽錯，英國牛津大學、跟佛朗西斯．克里克研究所，還有倫敦大學學院在 2024 年 3 月下旬公布，他們正在研發一款預防性的肺癌疫苗，就叫 LungVax。它所使用的技術，和過往牛津大學協同阿斯特捷利康藥廠製造 COVID-19 AZ 疫苗時的方法相似。

他們已經募到一筆 170 萬英鎊的經費，預計未來兩年資金陸續全數到位，第一批打算先試生產 3000 劑。不過，關於這款肺癌疫苗，目前透露的消息還不多，我們挺健康會持續追蹤這方面研究的進展。

在疫苗出來之前，我們還有第二個對策：抗發炎。發炎和肺癌有什麼關係呢？這就要先回到一個問題：為什麼空污會提高得肺癌的機率呢？

一個很直觀又有力的推測是，空污會導致肺部細胞 DNA 突變，因此而催生出腫瘤。

但是修但幾勒，科學要嚴謹，不能只看結果。科學史上發生過很多次表象和真實截然不同的事件，空污和肺癌會不會也是這樣？

2023 年 4 月《Nature》的一篇封面故事，明確地說：Yes！肺癌真的和我們想的不一樣。

其實早在 1947 年，就有以色列生化學家貝倫布魯姆（Isaac Berenblum）質疑主流觀點，他提出的新假設是：除了 DNA 突變以外，癌細胞還需要其他條件才能坐大。用白話說，就是肺癌是個會兩段變身的遊戲副本頭目，正常細胞先發生變異，接著再由某個條件「扣下扳機」，突變細胞才會壯大成腫瘤。

也就是説，只要攔住任一個階段，就有機會能防範肺癌。假如這論點正確，全球肺癌防治的方向將會直角轉彎。

《Nature》的研究支持這個假說，扭轉了過去 70 多年來的看法。在這項里程碑研究中，臺灣也是要角。

時間回到 2020 年，《Nature Genetics》上發表了一份針對 20 種致癌物質的研究報告，包括鈷、三氯丙烷和異丙苯等，但注意，這研究指出這些致癌物大多沒有增加實驗鼠的 DNA 變異量。

這個現象實在太違反直覺，過了 3 年，疑團還是懸而未決。直到《Nature》的跨國研究出爐，才解開部分謎底。

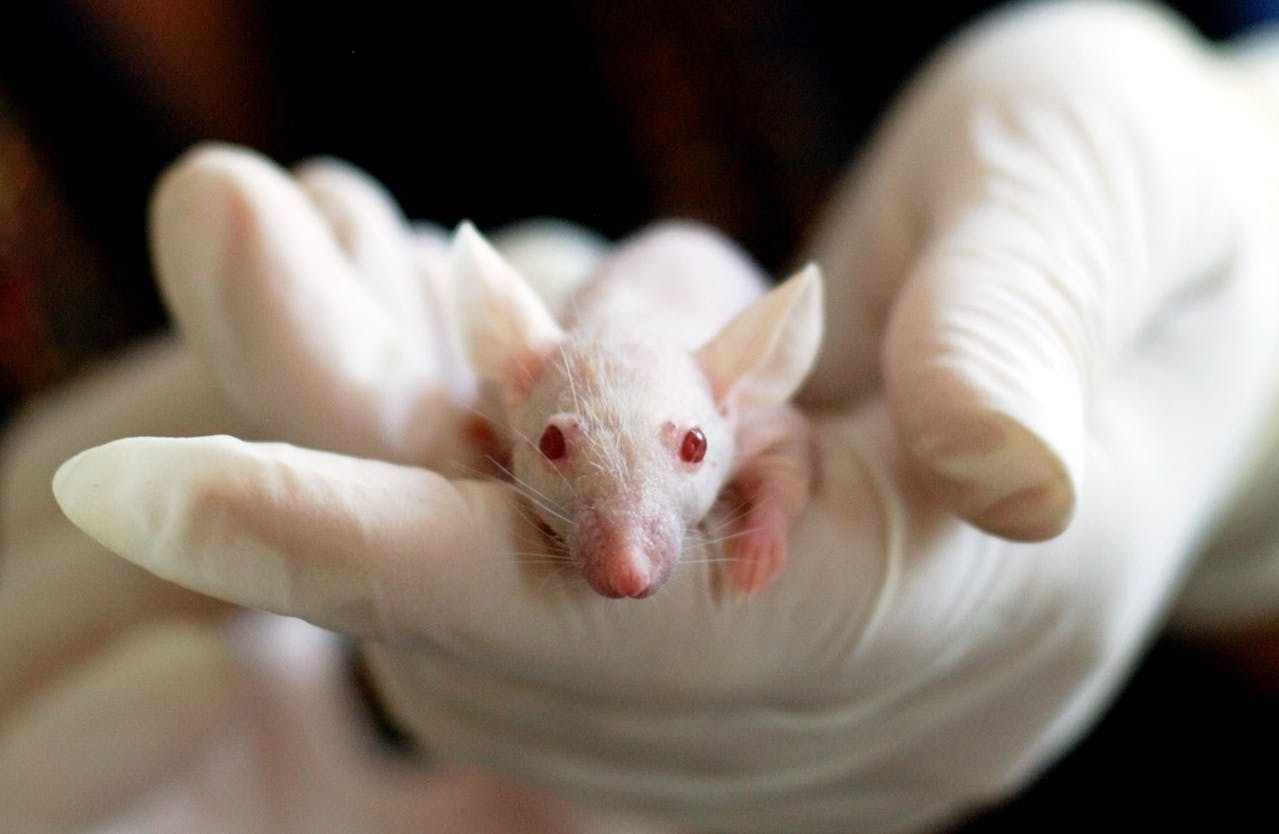
英國倫敦佛朗西斯．克利克研究所主導 2023 年的一項研究，他們鎖定對象為肺腺癌。肺腺癌是典型「不吸菸的肺癌」，台灣每 4 個肺癌病人就有 3 人是肺腺癌，尤其是女性肺腺癌患者有高達九成不抽菸。 為了抽絲剝繭探明空污和肺癌的關係，研究團隊聚焦在肺腺癌患者常發生的表皮生長因子受體基因變異，縮寫 EGFR。他們收集英國、加拿大、韓國和臺灣四國大約 3 萬 3 千名帶有 EGFR 突變的病人資料，進行深入分析，並且發現 PM2.5 和肺腺癌發生率有顯著關聯。研究團隊進一步用小鼠做試驗，把小鼠分成吸入和未吸入 PM2.5 兩組，結果發現吸入組更容易長出惡性腫瘤。

到目前為止都還不算太意外，然而，團隊切下肺部細胞、分析 DNA 以後發現，DNA 的突變量居然沒有明顯增加！但是有另一件事發生了：堆積在肺的 PM2.5 顆粒會吸引免疫細胞從身體各處聚集過來，並分泌一種叫做 IL-1β 的發炎因子，導致肺組織發炎。

這下子有趣了，根據克利克研究所團隊的檢驗結果，估計每 60 萬個肺部細胞有 1 個帶有 EGFR 突變，這些細胞在發炎環境裡會快馬加鞭生長。相反的，當他們給小鼠注射抑制 IL-1β 的抗體，肺癌發病率就跟著下降。 《Nature》一篇評論引述美國加州大學舊金山分校分子腫瘤學專家波曼（Allan Balmain）的看法。他總結說，空污致癌的主要機制，可能不是因為空污誘發了新突變，而是持續發炎會刺激原本已帶有突變的細胞生長。換句話說，本來在熟睡的壞細胞會被發炎反應「叫醒」。

這會給肺癌防治帶來巨大衝擊，這樣一來，問題就從「用公衛或醫療方法防止 DNA 變異」變成了「如何抑制發炎」。

人體的細胞每天不斷分裂，用新細胞替換老舊細胞。但是這就像工廠生產線，良率無法百分百，組裝幾十萬產品難免會做出幾件瑕疵品，也就是帶有基因突變的細胞。換句話說，從自然界角度來看，DNA 變異是一種自發現象，醫療手段實際上幾乎不可能阻止。

但是，降低發炎卻是有可能做到的，例如注射抑制 IL-1β 因子的抗體。不過，就公共衛生來說，要給幾千萬人施打抗發炎因子藥物根本不切實際，因為太花錢，而且也可能造成其他的副作用。 波曼在《Nature》評論裡建議，透過簡易可行的飲食方式來降低體內發炎，或許有機會減少某些癌症的風險。這也就是說，科學家應該重新回來審視，怎樣把每天的生活點滴點石成金變成防癌手段。

這也等於預告了肺癌的下一階段研究方向，除了內科、外科醫療科技持續精進，尋求預防惡性疾病的最佳飲食要素，也成為聚焦重點。

留言告訴我們你的想法吧，如果你覺得這集的內容特別實用，記得分享給你的親朋好友！

歡迎訂閱 Pansci Youtube 頻道 獲取更多深入淺出的科學知識！